Линейное программирование. Подготовка к зачёту. часть 1.ЛП. 1. методы решения задач линейного программирования
 Скачать 1.44 Mb. Скачать 1.44 Mb.
|
1.4 Симплексный метод решения задачи линейного программированияСимплексный метод (симплекс-метод) решения задач линейного программирования относится к числу итерационных методов, а это означает, что в процессе поиска оптимального решения выполняемые в определенной последовательности однотипные вычислительные процедуры повторяются до тех пор, пока это решение не будет получено. В основе построения симплексного метода лежит положение о том, что оптимальному решению всегда соответствует одна из угловых (или экстремальных) точек области допустимых решений. Исходя из этого, в вычислительной процедуре симплексного метода реализуется упорядоченный процесс, при котором, начиная с некоторой начальной допустимой угловой точки, осуществляются переходы от одной допустимой угловой ТОЧКИ ПДР к другой. Каждый очередной переход осуществляется только в смежную (соседнюю) точку, при этом переход к предшествующей, уже пройденной экстремальной точке производиться не может, Перед каждым очередным переходом к смежную точку выполняется проверка на оптимальность той точки, которая в данный момент достигнута процедурой поиска оптимального решения. Переход от геометрического способа решения задачи линейного программирования к симплекс-методу лежит через алгебраическое описание крайних точек пространства решений. Для реализации этого перехода сначала надо привести задачу линейного программирования к стандартной форме, преобразовав неравенства ограничений в равенства путем введения дополнительных переменных. Дополнительные переменные вводятся со знаком «+», если неравенства имеют вид «≤». В случае наличия неравенств, имеющих вид «≥», дополнительные переменные в них вводят со знаком «–». Получим систему из m линейных уравнений и n неотрицательных переменных, при этом количество уравнений m всегда меньше или равно количеству переменных n. В алгебраическом представлении кандидаты на оптимальное решение (т. е. те же угловые точки в графическом представлении) определяются из системы линейных уравнений следующим образом. Полагаем n–m переменных равными нулю и решаем систему из m уравнений относительно оставшихся m переменных. Если решение этой системы единственно, то оно соответствует угловой точке пространства решений. Для поиска оптимального решения необходимо проанализировать вес угловые точки пространства допустимых решений. Для этого надо рассмотреть все комбинации n–m переменных, приравнять их к нулю и затем найти решение полученной системы уравнений. Оптимальное решение, которое доставляет наилучшее значение целевой функции, будет среди допустимых угловых точек. Для полного перехода к алгебраическому методу решения задач линейного программирования необходимо назвать угловые точки разного типа на «алгебраическом» языке. Переменные в количестве п – т, которые полагаются равными нулю, называются и с базисными переменными. Если оставшиеся m переменные имеют единственное решение, то и этом случае они называются базисными переменными. а совокупность значений, которые они получают в результате решения системы уравнений, составляют базисное решение. Если при этом все переменные принимают неотрицательные значения, то такое базисное решение является допустимым; в противном случае – недопустимым. Рассмотрим метод решения задачи линейного программирования с применением симплексных таблиц. С помощью дополнительных переменных перейдем к системе уравнений. В данном случае дополнительные переменные вводятся со знаком «+». так как вес неравенства имеют вид «≤». Запишем уже рассмотренную выше задачу и стандартной форме. Максимизировать Z=5x1 + 4х2 +0s1+0s2+0s3+0s4, п 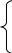 ри ограничениях: ри ограничениях: 6х1 + 4x2 + s1 ≤ 24, 1х1 +2x2 + s2 ≤ 6, -х1 + х2 + s3 ≤ 1, х2 + s4 ≤ 2, х1, х2, s1, s2, s3, s4 ≥0. где sl, s2, s3, s4 – дополнительные переменные. Целевую функцию представим в виде уравнения Z – 5x1 – 4х2 =0 и перейдем к табличной форме представления задачи (таблица 1.2). В ячейках таблицы расположены коэффициенты при соответствующих переменных. Таблица 1.2 – Первая симплекс-таблица
Первая симплекс-таблица соответствует начальной итерации симплекс-метода, который начинается из точки (х1, х2)=(0,0), что определяет множества базисных и небазисных переменных. Небазисные (нулевые) переменные: (х1, х2). Базисные переменные: ( s1, s1, s3, s4 ). Для точки (х1, х2) = (0.0) получим решение: Z=0, s1=24, s2=6, s3=1, s4=2. В таблице 1.2 базисные переменные перечислены в левом столоне «Базис», а их значения приведены в правом столбце «Решение». Рассмотренное начальное решение не является оптимальным, поскольку переменные х1, и х2 равны нулю, а возрастание их приводит к увеличению значения целевой функции. При этом в формуле целевой функции коэффициент при переменной х1, больше, чем коэффициент при x2, тогда в число базисных переменных следует ввести переменную х1. Но симплекс-таблице переменная, вводимая в число базисных, определяется среди множества небазисных как переменная, имеющая наименьший отрицательный коэффициент в Z -строке. Если так случится, что все коэффициенты в Z -строке будут неотрицательными, то дальнейшее увеличение значения целевой функции будет невозможно; это будет означать, что достигнуто оптимальное решение. В виду того, что в число базисных вводится переменная х1, возникает необходимость определить переменную, исключаемую из числа базисных. Чтобы определить исключаемую переменную, надо вычислить точки пересечения всех функций ограничений с положительным направлением оси x1. Координаты этих точек пересечения можно вычислить как отношения правых частей равенств (значение в столбце «Решение») к коэффициентам при переменной х1, в этих равенствах, как показано в таблице 1.3. Таблица 1.3 – Фрагмент первой симплекс-таблицы
|
