Линейное программирование. Подготовка к зачёту. часть 1.ЛП. 1. методы решения задач линейного программирования

• Название: 1. методы решения задач линейного программирования
• Анкор: Линейное программирование
• Дата: 26.11.2022
• Размер: 1.44 Mb.
• Имя файла: Подготовка к зачёту. часть 1.ЛП.docx
• Тип: Документы; #813006
• страница: 7 из 9

В итоге получим новую симплекс-таблицу, соответствующую новому базисному решению
(x₁, s₂, s₃, s₄) (таблица 1.5).

В столбце «Решение» представлено новое базисное решение (х₁ = 4, s₂ = 2, s₃ = 5, s₄ = 2)
и новое значение целевой функции Z = 20.
Таблица 1.5 – Вторая симплекс-таблица

Базис	Z	х1	х2	s1	s2	s3	s4	Решение
Z	1	0	-2/3	5/6	0	0	0	20
х1	0	1	2/3	1/6	0	0	0	4
s2	0	0	4/3	- 1/6	1	0	0	2
s3	0	0	5/3	1/6	0	1	0	5
s4	0	0	1	0	0	0	1	2

Полученное базисное решение не является оптимальным, поскольку в Z -строке переменная х₂ имеет отрицательный коэффициент. Как и в первой симплекс-таблице, строку Z можно интерпретировать как уравнение: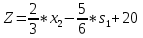



Соответственно увеличение значения переменной х₂ (ее текущее значение равно нулю) приведет к увеличению значения целевой функции. Поэтому переменная х₂ выбирается в качестве вводимой в базис (таблица 1.6).

Для определения исключаемой переменной вычислим отношения правых частей равенств, соответствующих ограничениям, к коэффициентам, стоящим при х₂ в этих равенствах (таблица 1.7).

Вычисления показывают, что минимальное неотрицательное отношение х₂=3/2 соответствует переменной s₂, которая становится исключаемой. Значения целевой функции составит: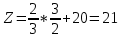



Таблица 1.6 – Модифицированная вторая симплекс-таблица

Базис	Z	х1	х2	s1	s2	s3	s4	Решение
Z	1	0	- 2/3	5/6	0	0	0	20
х1	0	1	2/3	1/6	0	0	0	4
s2	0	0	4/3	- 1 /6	1	0	0	2
s3	0	0	5/3	1/6	0	1	0	5
s4	0	0	1	0	0	0	1	2
			Ведущийстолбец

Ведущая строка




В этой ситуации ведущей строкой будет s₂ -строка, а ведущим столбцом будет столбец, соответствующий переменной х₂. Ведущий элемент равен 4/3 (таблица 1.7).
Таблица 1.7 – Фрагмент второй симплекс-таблицы

Базис	Коэффициенты при х2	Решение	Отношение (точка пересечения)
х1	2/3	4	х2=4/(2/3)=6
s2	4/3	2	х2=2/(4/3)=3/2 (минимум)
s3	5/3	5	х2=5/(5/3)=3
s4	1	2	х2=2/1=2

Вычислим элементы третьей симплекс-таблицы.

1	Элемент новой ведущей х2 - строки	=	Элемент текущей ведущей s2 - строки
			4/3
2.1	Элемент новой Z -строки	=	Элемент текущей Z -строки – (–2/3)*( Элемент новой ведущей строки)
2.2	Элемент новой x1 -строки	=	Элемент текущей x1 -строки – (2/3)*( Элемент новой ведущей строки)
2.3	Элемент новой s3 -строки	=	Элемент текущей s3 -строки – (5/3)*( Элемент новой ведущей строки)
2.4	Элемент новой s4 -строки	=	Элемент текущей s4 -строки –1*( Элемент новой ведущей строки)

В итоге получим новую симплекс-таблицу, соответствующую новому базисному решению (x_l,x₂,s_i,s₄) (таблица 1.8).
Таблица 1.8 – Третья симплекс-таблица

Базис	Z	х1	х2	s1	s2	s3	s4	Решение
Z	1	0	0	3/4	] /2	0	0	21
х1	0	1	0	1/4	-1/2	0	0	3
х2	0	0	1	- 1/8	3/4	0	0	3/2
s3	0	0	0	3/3	-5/4	1	0	5/2
s4	0	0	0	1/8	-3/4	0	1	1/2

Поскольку Z -строка не имеет отрицательных коэффициентов, со­ответствующих небазисным переменным s, и s₂, полученное оптимальное решение представлено в таблице 1.9 и совпадает с результатом решения задачи линейного программирования геометрическим методом (рисунок 1.2).
Таблица 1.9 – Результаты применения симплексного метода

Переменные задачи	Оптимальные значения	Интерпретация
х1	3	Ежедневно следует производить 3 т краски для наружных работ
х2	3/2	Ежедневно следует производить 1,5 т краски для внутренних работ
Z	21	Ежедневный доход составляет 21 тыс. у. е.

В рассмотренном примере проводился поиск максимума целевой функции. В случае минимизации целевой функции Z исключаемые переменные определяются точно так же, как и при ее максимизации. Вводимая переменная выбирается как небазисная с наибольшим по­ложительным коэффициентом в Z -строке симплекс-таблицы, а минимум целевой функции будет достигнут тогда, когда все коэффициенты в Z -строке будут неположительными.