Повышение виброустойчивости инструментальных систем станков. ТАММ-22_МетелевМА_реф1(повышение виброустойчивости инструменталь. 1. Виды колебаний при обработке резанием. 3 Гипотезы возникновения автоколебаний при резании. 6

• Название: 1. Виды колебаний при обработке резанием. 3 Гипотезы возникновения автоколебаний при резании. 6
• Анкор: Повышение виброустойчивости инструментальных систем станков
• Дата: 17.09.2022
• Размер: 2.36 Mb.
• Имя файла: ТАММ-22_МетелевМА_реф1(повышение виброустойчивости инструменталь.docx
• Тип: Реферат; #682106
• страница: 3 из 7

2.3 Гипотеза Соколовского.

Причиной автоколебаний, по мнению Соколовского, является переменная величина радиальной компоненты силы резания Py при периодическом сближении и удалении детали и инструмента.

Он рассматривает колебания, нормальные к обрабатываемой поверхности (рис.2.3.1). Именно колебания этого направления влияют на волнистость обрабатываемой поверхности.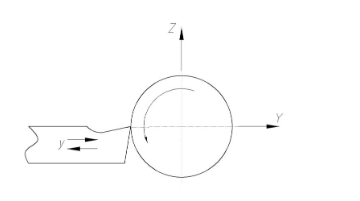



Рисунок 2.3.1 Радиальные колебания резца.

Сила Py при точении в первом предположении определяется выражением:

2.3.1

где Сr–коэффициент, зависящий от рода обрабатываемого материала, геометрии инструмента и некоторых других факторов; B –ширина среза; s –толщина среза; q –показатель степени, имеющий значение меньшее единицы, приближенно q=0,75. При возникновении колебаний мгновенная толщина среза не будет равна толщине среза (s) при спокойной работе, а будет циклически изменяться. Принимая, что при отсутствии вибраций y=0, получим простое выражение:

2.3.2

где Sмгн. – мгновенное значение толщины среза.

Если считать, что формула 1 справедлива для системы, находящейся в состоянии колебательного движения, мгновенное значение силы Py мгн. будет равно:

2.3.3

Простота полученного выражения является следствием предположения, что при быстром колебательном движении резца (как при его врезании, так и при отходе) справедливы те же зависимости, которые были получены опытным путем для значения усилий в квазистатическом состоянии системы.

Очевидно, что при однозначном виде зависимости Py=f(y), т.е. если каждому данному значению y соответствует одно, вполне определенное значение Py, то сила Py не может поддерживать автоколебательный процесс. Работа такой силы за полный цикл (врезание и отход резца), равная:

2.3.4

где–значение y0, соответствующее началу и концу периода, равна нулю, вне зависимости от характера изменения y в функции времени.

Графически зависимость Py=f(y) изображается линией AB, показанной пунктиром на рисунке 2.3.2

В реальных системах необходимо учитывать присутствие диссипативных сил, которые за каждый цикл поглощают некоторое количество энергии. Эта энергия может быть восполнена только за счет работы силы резания, из чего следует, что Py=f(y) есть неоднозначная функция. Значение силы Py при врезании резца в металл должно быть меньше, чем при его отходе. (сплошные линии на рис. 2.3.2)



Рисунок. 2.3.2. Изменение силы резания в цикле колебаний по Соколовскому.

Различие усилий при врезании и при отталкивании Соколовский объясняет действием наклепа в слое, прилегающем к режущей кромке. «При врезании режущая кромка срезает свежие, слабо деформированные слои металла. При отталкивании режущая кромка срезает сильно деформированные, наклепанные слои металла с повышенной твердостью». Сравнение теоретических выводов с результатами экспериментов показало, что предложенная модель качественно описывает автоколебательный процесс при точении. Однако физический принцип, объясняющий наличие двузначности силы и отраженный в приведенной выше формулировке гипотезы, в действительности не существует.[8]

3. Влияние вибраций на точность и качество обработанной поверхности.

Автоколебания в сильной степени влияют на качество обработанной поверхности. С увеличением амплитуд автоколебаний пропорционально ухудшаются параметры шероховатости, растёт высота волнистости Wz, обработанной поверхности.

На рисунке 3.1 a, показана зависимость высоты волнистости Wz от амплитуды автоколебания (А) для процесса точения разных металлов. Эти зависимости представляют собой почти прямые линии.





Рисунок 3.1- Зависимости высоты волнистости и шероховатости от амплитуды колебаний.

Шероховатость обработанной поверхности, особенно её параметры и , также существенно зависят от амплитуды автоколебаний. На рис 3.1 б показана зависимость Ra от A для тех же условий резания. Эта зависимость менее чётка чем для Wz, т.к. шероховатость поверхности также зависит от режима резания, геометрии и износа инструмента, однако общая тенденция ухудшения параметров шероховатости с повышением амплитуды колебаний всегда сохраняется.

В результате расчётов получены адекватные математические модели, отображающие зависимость высоты волнистости о среднеарифметического отклонения профиля от интенсивности автоколебаний.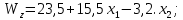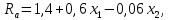





Где =[(A-60)/45,5] мкм; =[(f-600)/200] Гц.

На обе характеристики поверхности амплитуда и частота влияют по-разному: повышение амплитуды приводит к увеличению волнистости и шероховатости поверхности. Последнее ещё в большей степени наблюдается для процесса точения.[5, 30-31]

В ряде случаев силы инерции незначительны по сравнению с силами резания, упругости и сопротивления. В связи с этим, ограничиваясь исследованием влияния следа на поверхность резания и величины отставания изменения силы резания от изменения толщины среза (фазовой характеристики силы резания т) на волнистость обработанной поверхности, получим дифференциально-разностное уравнение.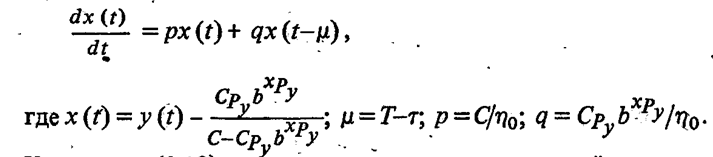

3.1

Уравнению 3.1 соответствует характерестический квазиполином.



Тогда, выбрав начальное возмущения в виде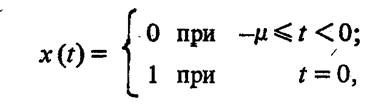



находим

3.2



Суммируя в равенстве 3.2 ряды справа получим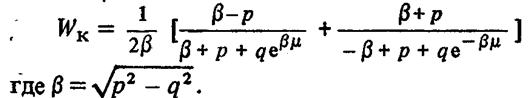



После преобразований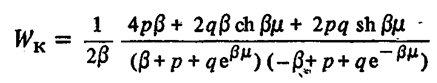

3.3

Выражение (3.3) после подстановки в него значений р, Q, а в используется для оценки влияния свойств обрабатываемого материала, режимов резания, параметров упругой системы технологической, геометрических и конструктивных параметров режущего инструмента на волнистость об обработанной поверхности.

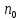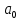На рис. 2.8 представлены зависимости квадратичного критерия волнистости обработанной поверхности от фазовой характеристики силы резания τ и коэффициента сопротивления . Исходное данные для расчета:C= 0,55 10^7 Н/м; v = 0,5 м/с; b = 3,5, . =0,2 мм. Расчеты проведены применительно к трем маркам обрабатываемых материалов.

Зависимость критерия волнистости от величины τ экстремальна. Максимальное значение Wk соответствует величине отставания τ = π/2 или γ = Тк/4. Увеличение коэффициента сопротивления ведет к резкому снижению волнистости.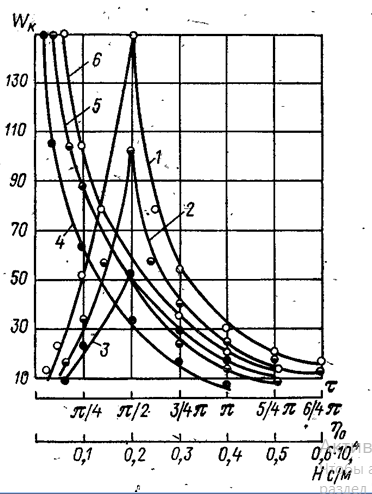



Рисунок 3.2 - Зависимости квадратичного критерия волнистости обработанной поверхности от фазовой характеристики силы резания (отставания τ) и коэффициента сопротивления .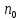

Анализ уравнения (3.2) приводит к выводу, что с помощью этого критерия расчетным путем можно прогнозировать параметры волнистости, изменяя режим резания, параметры упругой технологической системы, а также геометрию режущего инструмента. Теоретическое прогнозирование параметров волнистости обработанной поверхности создает возможность управления волнистостью поверхности деталей при их обработке.

Следует также отметить, что давно назрела необходимость разработки государственного стандарта на волнистость, который должен отражать количественные характеристики поверхности, так как волнистость оказывает существенное влияние на эксплуатационные характеристики деталей. Кроме рекомендованного среднеарифметического значения высоты волнистости Wz целесообразно оценивать волнистость с учетом квадратичного критерия Wк, расчет которого можно производить на основе уравнений автоколебательного процесса. [5, 32-35]

Сила резания 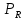и ее проекции (Рү, Pz) являются нелинейными величинами.

Во-первых, они нелинейно зависят от толщины среза a. Для их выражения можно использовать зависимости

3.4

3.5

где K, Ao, Bo, yр - постоянные, зависящие от геометрии инструмента и свойств обрабатываемого материала; b – ширина среза

Процесс резания как процесс пластической деформации обладает определенной инерционностью. Иными словами, изменение силы резания отстает по времени от изменения толщины срезаемого слоя на некоторую величину τ.

Если заданная толщина среза , то текущее значение составляющих силы резания на основании формул (3.4) и (3.5) можно выразить в виде

3.6

3.7

где х - координата зоны резания.

В равенствах (3.6) и (3.7) не учтено влияние перемещений вдоль оси OZ на изменение толщины среза. Здесь также не учтено влияние работы «по следу» при от предыдущего оборота изделия (или предыдущего зуба фрезы).

Однако почти во всех реальных процессах работа производится «по следу», при этом наличие следа на поверхности резания весьма существенно влияет на процесс автоколебаний. Влияние следа может быть учтено в выражениях (3.6), (3.7) вторичным запаздыванием - Т. Тогда равенства (3.6), (3.7) принимают вид

(3.8)

(3.9)

где Т - время одного оборота детали при точении или борштанги при расточке.[5, 46-47]

Важным показателем качества обработанной поверхности является наклёп, оказывающий значительное влияние на эксплуатационные характеристики деталей. Равномерны наклёп поверхностного слоя оказывает благоприятное влияние на предел усталостной прочности деталей, работающих при нормальных температурах.

Ниже приведены результаты исследования глубины и степени наклепа поверхностного слоя в зависимости от амплитуды автоколебаний.





Рисунок 3.2 – Зависимость глубины наклёпа от амплитуды колебаний.
Кривые 1-5 (рис 3.2а) указывают на зависимость глубины наклепа h от удвоенной амплитуды колебаний. Кривые 6 и 7 выражают зависимость степени наклепа N от величины 2A. Кривые 1-4, 6 относятся к обработке стали 08х15н5д2т а кривые 5 и 7 – к обработке стали 12Х18Н9Т.

То есть при наложении на режущий инструмент вынужденных ультразвуковых колебаний с частотой от f=15 до 35 кГц и амплитудой до 10 мкм приложит к увеличению степени наклепа до 40% и глубины наклепа до 100 мкм и более. Автоколебаний с частотой 240-300 Гц и амплитудой А-70 мкм приводит к увеличению степени наклепа до 100 мкм и более.

Следовательно, циклический характер взаимодействий задней поверхности инструмента с поверхностью резания при вибрации, существенно упрочняет поверхностный слой.

Из всего этого можно сделать вывод: если есть возможность управлять основными параметрами колебаний, то, имея определённые значения частоты и амплитуды колебаний, можно будет получить более точную и прочную поверхность. [5, стр 30-35]