задания по Герасимову. 1. задание из трех вопросов а
 Скачать 371.42 Kb. Скачать 371.42 Kb.
|
|
Задача 5.12. Определите принадлежность и вид каждого стандарта из списка, приведенного ниже, пользуясь приложением 11 и при необходимости источниками, заполните таблицу следующего вида:
BS EN ISO 11987:1998*BS 7208-14:1998 Оптика офтальмологическая. Контактные линзы. Определение срока годности при хранении. BS EN 50106:1997 Приборы электрические бытового и аналогичного назначения. Безопасность. Частные правила для типовых испытаний приборов, на которые распространяются требования стандартов BS EN 60335-1 и BS EN 60967. BS 9222:2007 Персональное финансовое планирование. Руководство по применению BS ISO 22222 и оценка соответствия. PD 6689:2009 Поверхностная обработка. Руководство по использованию BS EN 12271. BS 0-1:2005 Стандарт по стандартизации. Разработка стандартов. Технические условия. BS IEC 60050-101:1998 Международный электротехнический словарь. Математика. CAC/GL 3-1989 Продукты пищевые. Руководящие указания по простой оценке уровня потребления пищевых добавок. DIN EN 61549-2005 Лампы различных видов. DIN 66341-1993 Информационные технологии. Компьютерная графика. Эталонная модель. OEVE/OENORM EN 45020:2007 Стандартизация и связанная с ней деятельность. Основной словарь терминов. Трехъязычная версияISO/IEC 7810:2003 Карточки идентификационные. Физические характеристики. ISO 12:1987 Авиация и космонавтика. Трубопроводы. Идентификация. NF ISO 5626-1994 Бумага. Определение сопротивления излому. 6. ОСНОВЫ ТЕХНИЧЕСКИХ ИЗМЕРЕНИЙ ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ Задача 1. Отсчет по равномерной шкале прибора с пределами от нулевой отметки до 50 А составил 25 А. Пренебрегая другими видами погрешностей, оценить пределы допускаемой абсолютной погрешности этого отсчета при условии, что класс точности прибора равен: а) 0,02/0,01; б) 0,5; 0,5 в) . Решение. а). При классе точности прибора 0,02/0,01, при x = 25 А, XK= 50 А, с = 0,02, d = 0,01 (учитывая, что относительная погрешность выражается в процентах) получим 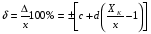 , ,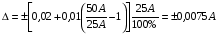 . .б). Для класса точности 0,5, учитывая, что нормирующее значение 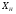 равно пределу измерений 50А, получаем равно пределу измерений 50А, получаем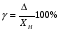 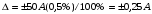 . .0,5 в). Для прибора класса точности 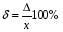 ; ; 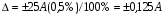 . .Задача 2. Для электромеханических измерительных приборов магнитоэлектрической системы класса точности 0,5 глубина ремонта составляет от 0,3…0,4; частота метрологических отказов на момент изготовления СИ ≈ 0,11 год -1, ускорение процесса старения ≈ 0,19 год -1. Требуется определить срок службы таких приборов и общее число отказов. Решение. 1. 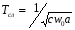 , , 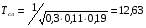 года. года.2. 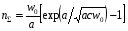 . .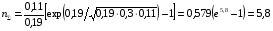 . . Задача 3. При диагностировании топливной системы автомобиля результаты пяти измерений расхода топлива составили 22, 24, 26, 28 и 48 л/100 км. Последний результат ставим под сомнение. Проверить, не является ли он промахом, используя критерии Романовского и Диксона, при значимости P= 0,05. Решение. 1. 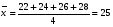 л/км; л/км;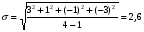 л/100 км. л/100 км.По критерию Романовского при P=0,05 и n=4, 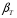 =1,71: =1,71: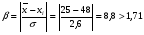 . .Данный критерий свидетельствует о необходимости отбрасывания последнего результата. 2. Составим вариационный ряд из результатов измерений расхода топлива: 22, 24, 26, 28, 48 л/100 км. Для последнего члена рассчитаем критерий Диксона: 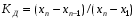 = (48 – 28)/(48 – 22) = 20/26 ≈ 0,77. = (48 – 28)/(48 – 22) = 20/26 ≈ 0,77.Для q=0,05 и n=4, 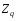 =0,76. Так как =0,76. Так как 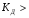 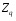 (0,77>0,76), данный критерий также свидетельствует о необходимости отбрасывания последнего результата. (0,77>0,76), данный критерий также свидетельствует о необходимости отбрасывания последнего результата.ЗАДАЧИ Задача 6.1. По шкале амперметра с пределами измерения от 0…10А измеренное значение составило 2А. Определить значение абсолютной погрешности, если на циферблате прибора нанесено обозначение класса точности 2,5. 2,5 Как изменится значение, если обозначение класса точности было ? Задача 6.2. Определить срок службы СИ, если известно, что средняя стоимость одного ремонта этого прибора составляет 1200 рублей, стоимость нового такого прибора - 10000 рублей, частота метрологических отказов на момент изготовления - 0,11 год -1, ускорение процесса старения - 0,14 год -1. Задача 6.3. Определить срок службы СИ, если известно, что средняя стоимость одного ремонта этого прибора составляет 12000 рублей, стоимость нового такого прибора - 60000 рублей, частота метрологических отказов на момент изготовления - 0,15 год -1, ускорение процесса старения -0,03 год -1. Задача 6.4. Было проведено пять измерений напряжений в электросети. Получены следующие данные: 127,1; 127,2; 126,9; 127,8; 127,2 В. Используя критерий Романовского, проверьте результат 127,6 В, который отличается от остальных. Не является ли он промахом? Задача 6.5. Измерение силы тока дало следующие результаты: 10,07; 10,08; 10,20; 10,12; 10,16; 10,15; 10,13; 10,17; 10,10; 10,40 А. Используя вариационный критерий Диксона, проверьте, не является ли промахом последний результат. Задача 6.6. Изучить метрологические характеристики средств измерений, в частности, по паспортам и эксплуатационной документации ознакомиться с нормированными метрологическими характеристиками различных средств измерений. Работу оформить по следующей форме:
Задача 6.7. Познакомиться с методикой метрологической обработки результатов измерения какого-либо параметра материала, для чего: а) произвести измерение; б) вычислить среднее арифметическое значение параметра, среднее квадратическое отклонение, коэффициент вариации; в) рассчитать необходимую численность выборки, ошибку опыта, значение генеральной средней; г) проанализировать влияние различных факторов (объекта, субъекта, средства измерения) по результатам измерений. Задача 6.8. Введение контроля температуры в теплицах позволяет поддерживать необходимый тепловой режим, что приводит к повышению урожайности овощей не менее чем на 6 %. В теплицах выращивается 2000т овощей в год. Цена 1 кг овощей - 15 д. ед. Необходимо оценить, какие затраты на определение контроля температуры будут рациональны при условии их окупаемости в течение 1 года. Задача 6.9. Увеличение влажности угля на 1% снижает теплоту его сгорания на 1,25%. Определите возможные расчетные потери тепла из-за неправильного измерения влажности угля приборами, имеющими погрешность 3 % при уровне годовой добычи угля 900 млн т. Задача 6.10. Погрешность эксплуатируемых счетчиков электрической энергии составляет 1,5%. Какая экономия электроэнергии будет получена при переходе на счетчики с погрешностью 1%, если общая выработка электроэнергии в стране составляет 1000 млрд кВт - ч в год? Задача 6.11. При разработке автоматизированной системы контроля при обработке деталей для изготовления станков было выдвинуто требование, чтобы риск заказчика (вероятность необнаруженного брака) был не более 0,005, а риск изготовителя (вероятность ложной браковки) - не более 0,01. Какова при этом ожидается вероятность верного заключения о состоянии измеряемого параметра? Задача 6.12. Произведено 12 измерений одним прибором (без систематической ошибки) некоторой физической величины, причем исправленное среднее квадратическое отклонение случайных ошибок измерений оказалось равным 0,6. Найти точность прибора с надежностью 0,99. Задача 6.13. Точность работы станка-автомата проверяется по дисперсии контролируемого размера изделий, которая не должна превышать 02=0,1. Взята проба из случайно отобранных изделий, причем получены следующие результаты:
При уровне значимости 0,05 проверить, обеспечивает ли станок требуемую точность. Задача 6.14. В итоге пяти измерений длины стержня одним прибором (без систематических ошибок) получены следующие результаты (в мм): 95; 97; 105; 108; 109. Найти: 1) выборочную среднюю длину стержня; 2) выборочную и исправленную дисперсии ошибок прибора. Задача 6.15. Цена деления шкалы измерительного прибора равна 0,2. Показания прибора округляют до ближайшего целого деления. Найти вероятность того, что при отсчете будет сделана ошибка: а) меньшая 0,04; б) большая 0,05. Задача 6.16. Цена деления амперметра равна 0,1А. Показания округляют до ближайшего целого деления. Найти вероятность того, что при отсчете будет сделана ошибка, превышающая 0,02 А. Задача 6.17. Определить класс точности, погрешность измерения и окончательный результат измерения по предложенным рисункам шкал приборов (прилож. 5) Задача 6.18. Расшифруйте и объясните знаки, нанесенные на поверительные клейма, изображенные в прилож. 12 и 13, при необходимости обращаясь к ПР 50.2.007-2001. 7. СЕРТИФИКАЦИЯ ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ Задача 1. На сертификацию поступила партия продукции, для проверки веса методом случайной повторной выборки было отобрано 200 штук. По выборочным данным был установлен средний вес изделия 30 г при среднем квадратическом отклонении 4 г. С вероятностью 0,997 определить пределы, в которых находится средний вес изделий в генеральной совокупности. Решение. Пределы устанавливаются на основе следующих соотношений: 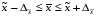 , (7.5) , (7.5)где 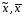 - генеральная и выборочная средние соответственно; - генеральная и выборочная средние соответственно;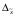 - предельная ошибка выборочной средней. - предельная ошибка выборочной средней.Предельную ошибку выборки можно найти по следующей формуле: 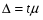 , (7.6) , (7.6)где 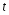 - коэффициент доверия, определяемый в зависимости от уровня вероятности; - коэффициент доверия, определяемый в зависимости от уровня вероятности;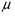 - средняя ошибка выборки. - средняя ошибка выборки.Средняя ошибка выборки при случайном повторном отборе определяется как 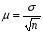 , (7.7) , (7.7)где 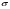 - выборочное (или генеральное) среднее квадратическое отклонение; - выборочное (или генеральное) среднее квадратическое отклонение;n – объем выборочной совокупности. При p = 0,997, t = 3 (по статистической таблице функции Лапласа). Предельная ошибка выборки равна 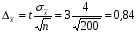 . .Соответственно пределы генеральной средней  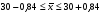 или или 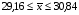 . .Следовательно, с вероятностью 0,997 можно утверждать, что средний вес изделий в генеральной совокупности находится в пределах от 29,16 до 30,84 г. Задача 2. С вероятностью 0,954 рассчитайте объем механической бесповторной выборки для определения соответствия поступившей на сертификацию партии продукции в количестве 1000 изделий, чтобы ошибка не превышала 2 % (среднее квадратическое отклонение по данным предыдущих обследований такой продукции равно 40). Решение. Необходимый объем выборки для случайной и механической выборки можно найти по следующим формулам: 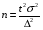 (повторный отбор); (7.8) (повторный отбор); (7.8) 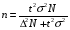 (бесповторный отбор), (7.9) (бесповторный отбор), (7.9)где N – объем генеральной совокупности. При p = 0,954, t= 2 (по статистической таблице функции Лапласа), таким образом, объем выборки равен 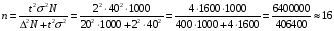 изделий. Задача 3. Необходимо определить степень согласованности мнений пяти экспертов при оценке качества семи объектов. Оценить значимость полученного коэффициента при α=0,05. Результаты ранжирования представлены в таблице.
Решение.
Среднеарифметическое число рангов 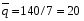 . .Определив сумму квадратов отклонений от среднего значения (S= 630), можно найти величину коэффициента конкордации 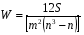 = =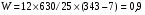 . .Мнения экспертов хорошо согласованы, т.к. значение коэффициента близко к 1. Для α =0,05 и γ = 6, χ2 = 12,592 оценим значимость коэффициента 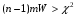 , , 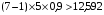 , , 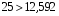 . .Условие выполняется, значит можно утверждать, что существует неслучайная согласованность в оценках экспертов. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
