задания по Герасимову. 1. задание из трех вопросов а
 Скачать 371.42 Kb. Скачать 371.42 Kb.
|
|
Нормативные значения параметров составляют: по температуре – не выше 30 С, по относительной влажности – не выше 75%. Определить методом относительных линейных оценок сводный относительный показатель неустойчивости процесса хранения. 4. ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ Задача 1.Дан фрагмент таблицы из ГОСТ-18242, определяющего методические принципы статистического контроля по альтернативному признаку (на примере усиленного одноступенчатого статистического контроля). Выписка из ГОСТа
На основе данного ГОСТа строятся стандарты правил приемки конкретной продукции. Решение. Рассмотрим пример приемки партии трикотажных изделий. Известно, что на контроль поступила партия трикотажных изделий объемом 100 шт.; в стандарте правил приемки на данную группу продукции "заложен" уровень дефектности 2,5 % и предусмотрен одноступенчатый контроль; изготовитель поставленной партии в прошлом неоднократно поставлял недоброкачественную продукцию. Отсюда следует, что приемка по качеству должна строиться по режиму усиленного контроля и по следующему плану: объем выборки – 20 шт., приемочное число – 1, браковочное число – 2. Если при проверке 20 шт. оказалось две (и более) забракованных единицы, то партию 100 шт. не принимают. Задача 2.Требуется по приведенным ниже данным построить контрольную карту контроля продукции за декаду. Исходные данные
Решение.Для построения контрольной карты необходимо определить значение среднего уровня дефектности, а также верхнюю и нижнюю границу регулирования. Среднее значение признака находится по средней арифметической формуле 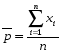 , (3.21) , (3.21)где 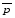 - среднее значение признака; - среднее значение признака;хi - индивидуальные значения признака; n- число индивидуальных величин. 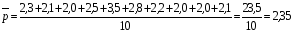 %. %.Для оценки контрольных границ (границ регулирования) применяется трехкратное среднеквадратичное отклонение (правило трех сигм). Данные для расчета границ регулирования представлены в таблице. 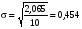 . .Верхняя граница регулирования: ВКП = 2,35+ 3*0,454 = 3,712. Нижняя граница регулирования: НКП = 2,35 - 3*0,454 = 0,988 (рис. 4.2). Результаты расчета границ регулирования
Поскольку точки, наносимые на контрольную карту, не выходят за границы регулирования, технологический процесс не требует дополнительного регулирования. Рис. 3.5. Контрольная карта для примера Задача 3. На заводе электроламп из партии продукции в количестве 1600 шт. ламп взято на выборку 1600 (случайный бесповторный отбор), из которых 40 оказались бракованными. Определить с вероятностью 0,997 пределы, в которых будет находиться процент брака для всей партии продукции. Решение. Определяется доля бракованной продукции по выборке w= 40/1600=0,25, или 25 %. При вероятности p= 0,997, t= 3,0 (2,97) (по статистической таблице функции Лапласа). Размер предельной ошибки 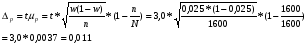 Таким образом, предельная ошибка составляет 1,1 %. Доверительные интервалы для генеральной доли с вероятностью p= 0,997 w-Δp<p<w+ Δp; 25 - 1,1<p< 25 + 1,1; 23,9 % <p<26,1 %. Задача 4. При контрольной проверке качества апельсинов произведена 10 % серийная выборка. Из партии, содержащей 50 ящиков апельсинов (вес ящиков одинаков), методом механического отбора взято 5 ящиков. В результате сплошного обследования находившихся в ящике апельсинов получили данные об удельном весе бракованных апельсинов. Результаты следующие:
Требуется с вероятностью 0,95 установить доверительные интервалы удельного веса бракованной продукции для всей партии апельсинов. Решение. Для установления доверительного интервала, в котором для всей партии поставки находится доля бракованной продукции, используется формула 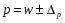 , (3.22) , (3.22)где 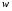 - удельный вес забракованной продукции; - удельный вес забракованной продукции;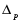 - абсолютная погрешность, - абсолютная погрешность, 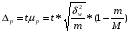 , (3.23) , (3.23)где δw2 - межсерийная (межгрупповая) выборочная дисперсия доли. При вероятности p = 0,95 t= 1,96 (см. табл. функции Лапласа). 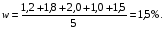 При расчете использована простая арифметическая, т.к. вес ящиков одинаков 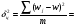 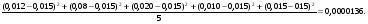 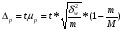 = 1,96* 0,00165* (1-5/50)=0,003, = 1,96* 0,00165* (1-5/50)=0,003,т.о. предельная ошибка составляет 0,3 %. Доверительные интервалы для генеральной доли с вероятностью p= 0,95. w-Δp<p<w+ Δp; 1,5 - 0,3<p< 1,5 + 0,3; 1,2 % <p<1,8 %. ЗАДАЧИ Задача4.1. По данным выборочных обследований качества строительно-монтажных работ доля дефектности при кирпичной кладке составляет 0,1. Какой должна быть численность выборки при проверке качества кирпичной кладки, чтобы ошибка выборки с вероятностью 0,954 не превышала 2%? Задача 4.2. Предприятие занимается производством и реализацией деталей. Вероятность того, что изготовляемая станком-автоматом деталь окажется бракованной, равна 0,01. Найти вероятность того, что среди 200 деталей окажется ровно 4 бракованных. Задача 4.3. В компании осуществляется контроль за выпуском изделий типа А два раза в день путем проверки изделий, попавших в случайную выборку объемом в 150 единиц. Каждый экземпляр считается либо прошедшим приемку, либо бракованным. Результаты последних 20 выборок изделий, изготовленных работниками соответствующей квалификации на машине, тщательно подготовленной и отлаженной, с использованием хорошего сырья, послужили основой для построения контрольной карты по доле брака. Ниже приводятся соответствующие результаты.
Требуется: используя приведенные выше данные, построить контрольные карты для доли брака р. Определить контрольные границы. Задача 4.4. Объем выполненных работ за отчетный квартал составил 680 тыс.руб. На основе проведенных контрольных обмеров и других материалов приемочной комиссии были выявлены следующие работы, выполненные с нарушениями технических условий и недоделками, тыс.руб.:
За поставку некачественных блоков и деталей взыскано с поставщиков 7,5 тыс. руб. С виновников, допустивших брак в работе, взыскано 3,5 тыс. руб. Определите:
Задача 4.5. По двум строительным управлениям имеются следующие данные о качестве строительства объектов общественного питания за отчетный год, м2:
Стоимость работ низкого качества, подлежащих переделке, составила по СМУ-8 28,6 тыс. руб.; СМУ-12 – 34 тыс. руб. Сопоставьте и проанализируйте показатели качества строительства по двум строительным организациям. Задача 4.6. Построить контрольную карту приема манометров за декабрь, если средняя доля дефектных изделий - 3,5, а значение среднего квадратического отклонения равно 0,918. Задача 4.7. Известно, что на контроль поступила партия изделий в количестве 200 штук, причем производитель неоднократно поставлял недоброкачественную продукцию. С уровнем дефектности 4,0 установить режим контроля и разработать программу контроля, используя выписку из ГОСТа. Изменятся ли выводы, если приемочный уровень дефектности снизить до 2,5%?
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||