50 математичесих задач. 50 экономических задач
 Скачать 164.45 Kb. Скачать 164.45 Kb.
|
|
Ответ: 1948353 рублей. Задача №3. Близнецы Саша и Паша положили в банк по 50 000 рублей на три года под 10% годовых Однако через год и Саша, и Паша сняли со своих счетов соответственно 10% и 20% имеющихся денег. Еще через год каждый из них снял со своего счета соответственно 20 000 рублей и 15 000 рублей. У кого из братьев к концу третьего года на счету окажется большая сумма денег? На сколько рублей? Решение: S=50000 – сумма вклада r% - годовые (ежемесячные) проценты, r=10% b=1+0,01r – коэффициент, b=1,1 n=3 года, х – действие Саша
0,9Sb3_ 20000b = 0,9*50000*1,331–20000*1,1 = 59895–22000 = 37895рублей Паша
0,8Sb3_ 15000b = 0,8*50000*1,331–15000*1,1 = 53240–16500 = 36740рублей 37895 – 36740 = 1155 рублей Ответ: у Саши на 1155 рублей. Задача №4. Миша и Маша положили в один и тот же банк одинаковые суммы под 10% годовых. Через год сразу после начисления процентов Миша снял со своего счета 5000 рублей, а еще через год снова внес 5000 рублей. Маша, наоборот, через год доложила на свой счет 5000 рублей, а еще через год сразу после начисления процентов сняла со счета 5000 рублей. Кто через три года со времени первоначального вложения получит большую сумму и на сколько рублей? Решение: S – сумма вклада r% - годовые (ежемесячные) проценты, r=10% b=1+0,01r – коэффициент, b=1,1 n=3 года, х – действие Миша
Sb3-5000b2+5000b = 1,331S-5000*1,21+5000*1,1=1,331S-6050+5500=1,331S-550 Маша
Sb3+5000b2-5000b = 1,331S+5000*1,21-5000*1,1=1,331S+6050-5500=1,331S+550 Ответ: у Маши на 1100 рублей. Задача №5. Гражданка Васильева вложила 44 млрд. рублей в два оффшорных банка на 3 года: часть денег в банк А, остальное в банк Б. Известно, что банк А ежегодно начисляет 10% годовых; банк Б в первый год начисляет 5% годовых, во второй – 10%, а в третий – 15%. Сколько рублей было вложено в каждый из банков, если через три года доход гражданки Васильевой от вложения денег составил 14 520 млн. рублей. Решение: S=44000млн – сумма вклада r% - годовые (ежемесячные) проценты, b=1+0,01r – коэффициент, n=3 года 1 банк
2 банк
1,331S+1,32825(44000-S)-44000=14520 1,331S-1,32825S=14520-58443+44000 0,00275S=77 S=28000 млн=28 млрд положила в 1 банк 44-28=16 положила во 2 банк Ответ: 28 млрд и 16 млрд рублей. Задача №6. 1 ноября 2017 года Николай открыл в банке счёт «Управляй», вложив S тысяч рублей (S – целое число) сроком на 4 года под 10% годовых. По договору с банком проценты по вкладу должны начисляться 31 октября каждого последующего года. 1 ноября 2019 года и 1 ноября 2020 года Николай планирует снять со счёта 100 тысяч и 50 тысяч рублей соответственно. 1 ноября 2021 года Николай собирается закрыть счёт в банке и забрать все причитающиеся ему деньги. Найдите наименьшее значение S, при котором доход Николая от вложений в банк за эти 4 года окажется более 70 тысяч рублей. Решение: S – сумма вклада r% - годовые (ежемесячные) проценты, r=10% b=1+0,01r – коэффициент, b=1,1 n=4 года, х – действие
Sb4_100b2-50b –S+150 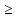 70 70S(b4_1)-100b2-50b +150 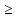 70 70S(1,14_1) 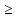 70-150+55+121 70-150+55+1210,4641S 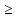 96 96S 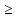 206,9 206,9S=207 Ответ: 207тысяч рублей. Задача №7. За время хранения вклада в банке проценты по нему начислялись ежемесячно сначала в размере 5%, затем 12%, потом 11 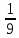 и, наконец, 12,5% в месяц. Известно, что под действием каждой новой процентной ставки вклад находился целое число месяцев, а по истечении срока хранения первоначальная сумма увеличилась на 104 и, наконец, 12,5% в месяц. Известно, что под действием каждой новой процентной ставки вклад находился целое число месяцев, а по истечении срока хранения первоначальная сумма увеличилась на 104 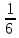 %. Определите срок хранения вклада. %. Определите срок хранения вклада.Решение: S – сумма вклада
Пусть n месяцев лежал вклад под 5%, m месяцев – под 12%, k месяцев – под 11 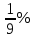 , p месяцев – под 12,5 %. , p месяцев – под 12,5 %.1,125p 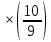 k k 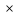 1,12m 1,12m 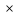 1,05n 1,05n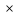 S = S = 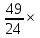 S S1,125p = 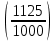 p = p = 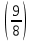 p= p= 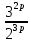 = = 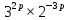 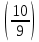 k= k= 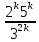 = = 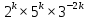 1,12m = 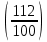 m = m = 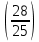 m= m= 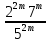 = = 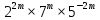 1,05n = 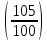 n = n = 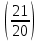 n= n= 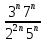 = = 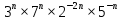 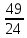 = =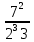 = = 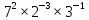 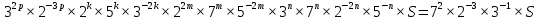 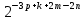 = = 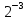 -2n+2m+k-3p=-3 n=1 -2n+2m+k-3p=-3 n=1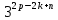 = = 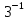 n-2k+2p = -1 m=1 n-2k+2p = -1 m=1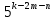 = = 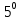 -n+k-2m = 0 k=3 -n+k-2m = 0 k=3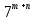 = = 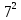 m+ n = 2 p=2 m+ n = 2 p=21+1+3+2 = 7 Ответ: 7 месяцев. Задача №8 Алексей приобрёл ценную бумагу за 7 тыс. рублей. Цена бумаги каждый год возрастает на 2 тыс. рублей. В любой момент Алексей может продать бумагу и положить вырученные деньги на банковский счёт. Каждый год сумма на счёте будет увеличиваться на 10 %. В течение какого года после покупки Алексей должен продать ценную бумагу, чтобы через тридцать лет после покупки этой бумаги сумма на банковском счёте была наибольшей? Решение:
На банковском счёте:
|

 1,125p×
1,125p×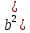 7000+(n-1)
7000+(n-1)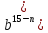 7000+(n-1)
7000+(n-1)