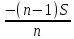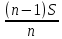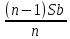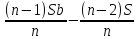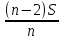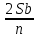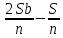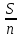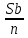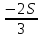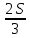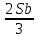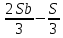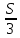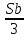50 математичесих задач. 50 экономических задач
 Скачать 164.45 Kb. Скачать 164.45 Kb.
|
Решение: Сумма кредита (S) , ставка (r) -5 %, b=1,05 n=?
Sb( 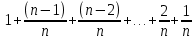 )-S )-S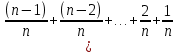 )=1,25S )=1,25SПо формуле суммы арифметической прогрессии получаем Sb* 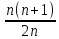 - S* - S*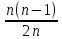 =1,25S /S =1,25S /Sb* 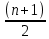 - -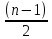 =1,25 =1,251,05*(n+1)-(n-1)=2,5 1,05n+1,05-n+1=2,5 0,05n=0,45 n=9 Ответ: 9 месяцев. 8 тип: Нестандартные задачи, связанные с кредитом. Задача 1. В июле 2016 года планируется взять кредит в размере 6,6 млн. руб. Условия возврата таковы: — каждый январь долг возрастает на r% по сравнению с концом предыдущего года. — с февраля по июнь необходимо выплатить часть долга. — в июле 2017, 2018 и 2019 годов долг остается равным 6,6 млн. руб. — суммы выплат 2020 и 2021 годов равны. Найдите r, если в 2021 году долг будет выплачен полностью и общие выплаты составят 12,6 млн. рублей. Решение: S=6,6 r% =? b=1+0,01r
1)Sb2-xb=x 2)3Sb-3S+2x=12,6 19,8b-19,8+2x=12,6 x=16,2-9.9b 1)6,6 b2 –(16,2-9,9b)b=16,2-9,9b 6,6 b2 -16,2b+9,9 b2 =16,2-9,9b 16,5 b2 -6,3b-16,2=0 165 b2 -63b-162=0 D=632+4•162•165=110889 b1=1,2 b2= -0,81не подходит по условию задачи. Ответ: r=20. Задача №2. 1 марта 2010 года Аркадий взял в банке кредит под 10% годовых. Схема выплаты кредита следующая: 1 марта каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Аркадий переводит в банк платеж. Весь долг Аркадий выплатил за 3 платежа, причем второй платеж оказался в два раза больше первого, а третий – в три раза больше первого. Сколько рублей взял в кредит Аркадий, если за три года он выплатил банку 2 395 800 рублей? Решение: Сумма кредита (S)-? Ставка (а)=10%, b=1,1 Количество лет (n) 3 года
x+2x+3x=2395800 6x=2395800 x=399300 Sb3_ хb2-2xb =3x Sb3-(3+2b+b2)x=0 S= Ответ: 1923000рублей. Задача №3. Анатолий решил взять кредит в банке 331000 рублей на 3 месяца под 10% в месяц. Существуют две схемы выплаты кредита. По первой схеме банк в конце каждого месяца начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 10%), затем Анатолий переводит в банк фиксированную сумму и в результате выплачивает весь долг тремя равными платежами (аннуитетные платежи). По второй схеме тоже сумма долга в конце каждого месяца увеличивается на 10%, а затем уменьшается на сумму, уплаченную Анатолием. Суммы, выплачиваемые в конце каждого месяца, подбираются так, чтобы в результате сумма долга каждый месяц уменьшалась равномерно, то есть на одну и ту же величину (дифференцированные платежи). Какую схему выгоднее выбрать Анатолию? Сколько рублей будет составлять эта выгода? Решение: Сумма кредита (S) – 331000 рублей Ставка (r) -10%, b=1,1 Аннуитетные платежи.
Sb3_ хb2-xb=x Sb3-(b2+b+1)x=0 3х=399300 Дифференцированные платежи.
Sb(1+ 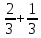 )-S )-S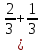 )=2Sb-S )=2Sb-S2*331000*1,1- 331000=331000*1,2=397200 399300 – 397200= 2100 Ответ: дифференцированные платежи, выгода 2100 рублей. Задача №4. Петр Иванович взял кредит на несколько лет и выплатил его равными ежегодными платежами по 200000 руб. При этом в начале каждого года сумма текущего долга увеличивалась на 10 %, а в конце года производился платёж. Если бы Петр Иванович не делал платежей, то за это время вследствие начисления процентов сумма кредита составила бы 928200 руб. На сколько лет был взят кредит? Решение: Кредит (S) Введём коэффициент b=1+0,01r
Sbn=928200, ставка (r) -10%, b=1,1 х= 200000рублей, аннуитетные платежи.
Sbn-xbn-1-xbn-2-…-xb2-xb-x=0 Sbn-x(bn-1+bn-2 +…+b2+b+1)=0 По формуле суммы геометрической прогрессии bn-1+bn-2 +…+b2+b+1= 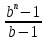 Sbn- x 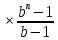 =0 =0928200- 200000 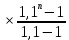 =0 =02000000 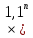 -1)=928200 -1)=928200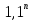 =1+0,4641, =1+0,4641, 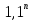 =1,4641 =1,4641n=4 Ответ:4 года. 3.2 Вклады. Задача №1. Владимир поместил в банк 3600 тысяч рублей под 10% годовых. В конце каждого из первых двух лет хранения после начисления процентов он дополнительно вносил на счет одну и ту же фиксированную сумму. К концу третьего года после начисления процентов оказалось, что размер вклада увеличился по сравнению с первоначальным на 48,5%. Какую сумму Владимир ежегодно добавлял к вкладу? Решение: S=3600 тысяч – сумма вклада r% - годовые (ежемесячные) проценты, r=10% b=1+0,01r – коэффициент, b=1,1 n=3 года, х =? – действие
Sb3+хb2+xb = 1,485S х(b2+b) = 1,485S - Sb3 х(1,21+1,1) = 1,485S – 1,331S 2,31х = 0,154*3600 2,31х = 554,4 х = 240 Ответ: 240000. Задача №2. Василий кладет в банк 1 000 000 рублей под 10% годовых на 4 года (проценты начисляются один раз после истечения года) с правом докладывать три раза (в конце каждого года) на счет фиксированную сумму 133 000 рублей. Какая сумма будет на счете у Василия через 4 года? (Решение с помощью формулы суммы геометрической прогрессии) Решение: S=1000000 – сумма вклада r% - годовые (ежемесячные) проценты, r=10% b=1+0,01r – коэффициент, b=1,1 n=4 года, х =133000 – действие
Sb4_+хb3+xb2+хb=Sb4_+хb(b2+b+1)=  |