50 математичесих задач. 50 экономических задач
 Скачать 164.45 Kb. Скачать 164.45 Kb.
|
|
Чтобы сумма на банковском счёте была наибольшей необходимо, чтобы процент (r) от стоимости ценной бумаги в n-ом году был больше, чем 2000 рублей
3.3 Задачи на оптимизацию. Задача №1. У фермера есть два поля, каждое площадью 100 гектаров. На каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 400 ц/га, а на втором — 300 ц/га. Урожайность свёклы на первом поле составляет 300 ц/га, а на втором — 400 ц/га. Фермер может продавать картофель по цене 10 000 руб. за центнер, а свёклу — по цене 11 000 руб. за центнер. Какой наибольший доход может получить фермер? Решение: Вся площадь: 100 га
Составим функцию полного дохода: ∑(x,k) = 4000000x+3300000kx→наиб Заметим, что x+kx=100, т.е. x= 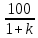 где k где k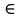 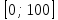 ∑(k) = 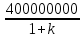 + +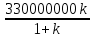 →наиб →наиб∑(k) = 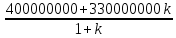 →наиб →наибВозьмём производную этой функции 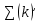 = = 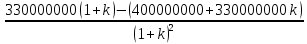 = = 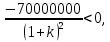 Значит функция убывает во всей области определения, т.е. принимает своё наибольшее значение при k=0. Это означает, что всё первое поле нужно засадить картофелем, при этом доход будет 4000000 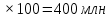 рублей рублей
Из второй таблицы видно, что свекла имеет, как большую урожайность, так и большую цену за центнер, следовательно, второе поле нужно засадить свеклой. При этом доход будет 400 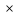 11000 11000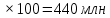 рублей рублейПолный доход составляет 400 млн + 440 млн = 840 млн рублей. Ответ: 840 млн рублей. Задача №2. У фермера есть два поля, каждое площадью 10 гектаров. На каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 500 ц/га, а на втором — 300 ц/га. Урожайность свёклы на первом поле составляет 300 ц/га, а на втором – 500 ц/га. Фермер может продать картофель по цене 5000 руб. за центнер, а свёклу — по цене 8000 руб. за центнер. Какой наибольший доход может получить фермер? Вся площадь: 10 га
Составим функцию полного дохода: ∑(x,k) = 2500000x+2400000kx→наиб Заметим, что x+kx=10, т.е. x= 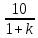 где k где k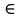 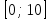 ∑(k) = 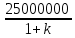 + +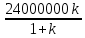 →наиб →наиб∑(k) = 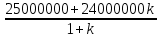 →наиб →наибВозьмём производную этой функции 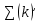 = = 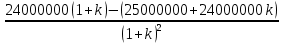 = = 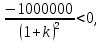 Значит функция убывает во всей области определения, т.е. принимает своё наибольшее значение при k=0. Это означает, что всё первое поле нужно засадить картофелем, при этом доход будет 2500000 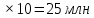 рублей рублей
Из второй таблицы видно, что свекла имеет, как большую урожайность, так и большую цену за центнер, следовательно, второе поле нужно засадить свеклой. При этом доход будет 500 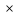 8000 8000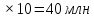 рублей рублейПолный доход составляет 25 млн + 40 млн = 65 млн рублей. Ответ: 65 млн рублей. Задача №3. Предприниматель купил здание и собирается открыть в нём отель. В отеле могут быть стандартные номера площадью 27 квадратных метров и номера «люкс» площадью 45 квадратных метров. Общая площадь, которую можно отвести под номера, составляет 981 квадратный метр. Предприниматель может поделить эту площадь между номерами различных типов, как хочет. Обычный номер будет приносить отелю 2000 рублей в сутки, а номер «люкс» — 4000 рублей в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своём отеле предприниматель? Решение: Общая площадь: 981
Составим функцию полного дохода: ∑(x,y) = 2000x+4000y→наиб Заметим, что 27x+45y 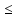 981, т.е. x 981, т.е. x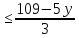 где y где y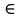 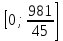 , т.е. y , т.е. y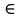 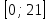 ∑(y) = 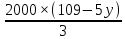 +4000y→наиб +4000y→наиб∑(y) = 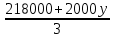 →наиб →наибВозьмём производную этой функции 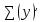 = = 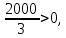 Значит функция возрастает во всей области определения, т.е. принимает своё наибольшее значение при y=21. Это означает, что номеров люкс будет 21. Проверим общую площадь: 45 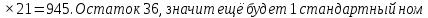 ер. При этом полный доход будет ер. При этом полный доход будет 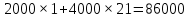 рублей. рублей.Ответ: 86000 рублей. Задача №4. Предприниматель купил здание и собирается открыть в нем отель. В отеле могут быть стандартные номера площадью 30 квадратных метров и номера «люкс» площадью 40 квадратных метров. Общая площадь, которую можно отвести под номера, составляет 940 квадратных метров. Предприниматель может определить эту площадь между номерами различных типов, как хочет. Обычный номер будет приносить отелю 4000 рублей в стуки, а номер «люкс» — 5000 рублей в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своем отеле предприниматель? Решение: Общая площадь : 940
Составим функцию полного дохода: ∑(x,y) = 4000x+5000y→наиб Заметим, что 30x+40y 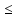 940, т.е. x 940, т.е. x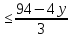 где y где y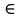 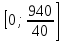 , т.е. y , т.е. y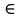 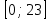 ∑(y) = 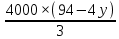 +5000y→наиб +5000y→наиб∑(y) = 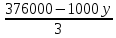 →наиб →наибВозьмём производную этой функции 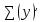 = = 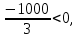 Значит функция убывает во всей области определения, т.е. принимает своё наибольшее значение при y=0. Это означает, что стандартных номеров будет 940 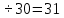 . Проверим общую площадь: 30 . Проверим общую площадь: 30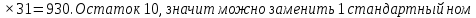 ер на номер люкс. При этом полный доход будет ер на номер люкс. При этом полный доход будет 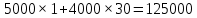 рублей. рублей.Ответ: 125000 рублей. Задача №5. Антон является владельцем двух заводов в разных городах. На заводах производится абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно t2 часов в неделю, то за эту неделю они производят t единиц товара. За каждый час работы на заводе, расположенном в первом городе, Антон платит рабочему 250 рублей, а на заводе, расположенном во втором городе, — 200 рублей. Антон готов выделять 900 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах? Решение: Оплата труда в неделю : 900000рублей
Составим функцию количества единиц товара: ∑(x,y) = x+y→наиб Заметим, что 250 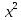 +200 +200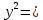 900000, т.е. x 900000, т.е. x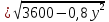 где y где y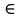 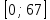 ∑(y) = 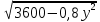 +y→наиб +y→наибВозьмём производную этой функции 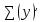 = = 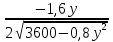 +1 = +1 =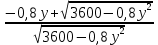 Найдём нули производной: 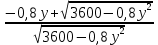 =0 =0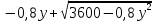 =0 =0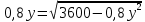 0,64 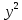 =(3600- =(3600-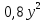 ) )1,44 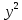 =3600 =3600y=50 Функция принимает своё наибольшее значение при y=50 (точка максимума). x 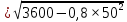 = =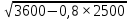 =40 =40Найдём количество единиц товара : 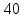 +50 = 90 +50 = 90Ответ: 90 единиц товара. Задача №6. Григорий является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 3t единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 4t единиц товара. За каждый час работы (на каждом из заводов) Григорий платит рабочему 500 рублей. Готов выделять 5 000 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах? Решение: Оплата труда в неделю: 5000000рублей
Составим функцию количества единиц товара: ∑(x,y) = 3x+4y→наиб Заметим, что 500 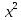 +500 +500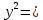 5000000, т.е. x 5000000, т.е. x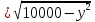 где y где y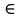 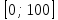 ∑(y) =3 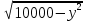 +4y→наиб +4y→наибВозьмём производную этой функции 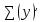 = 3 = 3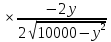 +4 = +4 =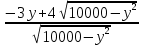 Найдём нули производной: 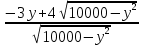 =0 =0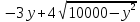 =0 =0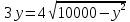 9 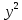 =16(10000- =16(10000-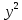 ) )25 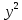 =1600000 =1600000y=80 Функция принимает своё наибольшее значение при y=80 (точка максимума). x 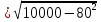 = =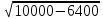 =60 =60Найдём количество единиц товара: 3 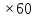 +4 +4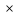 80 = 180+320 = 500 80 = 180+320 = 500Ответ: 500 единиц товара. Задача №7. Борис является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно t2 часов в неделю, то за эту неделю они производят t единиц товара. За каждый час работы на заводе, расположенном в первом городе, Борис платит рабочему 500 рублей, а на заводе, расположенном во втором городе, — 200 рублей. Борису нужно каждую неделю производить 70 единиц товара. Какую наименьшую сумму придётся тратить еженедельно на оплату труда рабочих? Решение: 70 единиц товара
Составим функцию еженедельной оплаты труда: ∑(x,y) = 500 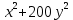 →наим →наимЗаметим, что x+y 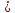 70, т.е. x 70, т.е. x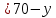 где y где y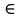 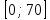 ∑(y) =500 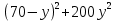 → наим → наим∑(y) =500 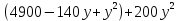 =700 =700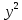 -70000y+2450000 -70000y+2450000Возьмём производную этой функции 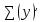 = 1400y-70000 = 1400y-70000Найдём нули производной: 1400y-70000=0 y=50 Функция принимает своё наименьшее значение при y=50 (точка минимума). x 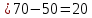 Найдём еженедельную оплату труда: 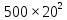 +200 +200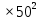 = 500 = 500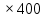 +200 +200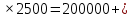 500000=700000 500000=700000Ответ: 700 тысяч рублей . Задача №8. Фёдор является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые приборы, но на заводе, расположенном в первом городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно 3t2 часов в неделю, то за эту неделю они производят t приборов; если рабочие на заводе, расположенном во втором городе, трудятся суммарно 4t2 часов в неделю, они производят t приборов. За каждый час работы (на каждом из заводов) Фёдор платит рабочему 1 тысячу руб. Необходимо, чтобы за неделю суммарно производилось 30 приборов. Какую наименьшую сумму придется тратить владельцу заводов еженедельно на оплату труда рабочих? Решение: 30 единиц товара
Составим функцию еженедельной оплаты труда: ∑(x,y) = 3000 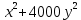 →наим →наимЗаметим, что x+y 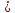 30, т.е. x 30, т.е. x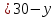 где y где y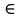 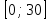 ∑(y) =3000 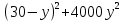 →наим →наим∑(y) =3000 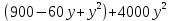 =7000 =7000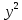 -180000y+2700000 -180000y+2700000Возьмём производную этой функции 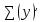 = 14000y-180000 = 14000y-180000Найдём нули производной: 14000y-180000=0 y = 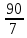 =12 =12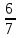 Функция принимает своё наименьшее значение при y=12 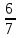 (точка минимума). (точка минимума). Пусть y=12, тогда x=18 Найдём еженедельную оплату труда: 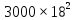 +400 +400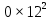 = 3000 = 3000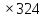 +4000 +4000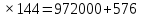 000=1548000 000=1548000Пусть y=13, тогда x=17 Найдём еженедельную оплату труда: 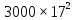 +400 +400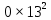 = 3000 = 3000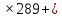 4000 4000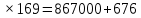 000=1543000 000=1543000Ответ: 1543000 рублей . Задача №9. В двух областях есть по 160 рабочих, каждый из которых готов трудиться по 5 часов в сутки на добыче алюминия или никеля. В первой области один рабочий за час добывает 0,1 кг алюминия или 0,1 кг никеля. Во второй области для добычи x кг алюминия в день требуется x2 человеко-часов труда, а для добычи у кг никеля в день требуется у2 человеко-часов труда. Для нужд промышленности можно использовать или алюминий, или никель, причём 1 кг алюминия можно заменить 1 кг никеля. Какую наибольшую массу металлов можно за сутки суммарно добыть в двух областях? Решение:
Из таблицы видно, что в первой области совершенно одинаковые условия добывания алюминия и никеля. Это означает, что в первой области алюминия и никеля будут добывать поровну по 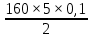 = 40 кг. Всего 80 кг. = 40 кг. Всего 80 кг.Во второй области: x2 +y2=160 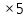 x2 +y2=800 x=20, y=20. Всего 40 кг. Ответ: 120кг. Задача №10. В двух шахтах добывают алюминий и никель. В первой шахте имеется 60 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 2 кг алюминия или 3 кг никеля. Во второй шахте имеется 260 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 3 кг алюминия или 2 кг никеля. Обе шахты поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 2 кг алюминия приходится 1 кг никеля. При этом шахты договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод? Решение: 60 человек по 5 часов в день
260 человек по 5 часов в день
Получаем, что всего алюминия производят 10x+15y никеля: 15(60-x)+ 10(260-y)=3500-15x-10y Так как для сплава необходимо , чтобы на2 кг алюминия приходился 1 кг никеля, то: 10x+15y=2(3500-15x-10y) 10x+15y=7000-30x-20y 40x=7000-35y x = 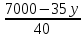 = = 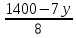 Составим функцию массы сплава: ∑(x,y) = 10x+15y +3500-15x-10y →наиб ∑(x,y) = 3500-5x+5y →наиб ∑(y) = 3500-5 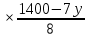 +5y →наиб +5y →наиб∑(y) = 3500-5 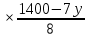 +5y →наиб +5y →наиб∑(y) = 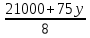 →наиб →наибВозьмём производную этой функции 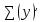 = = 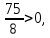 Значит функция возрастает во всей области определения, т.е. принимает своё наибольшее значение при наибольшем значении y. Так как x = 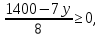 то 1400-7y то 1400-7y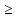 0 , y 0 , y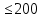 . .Проверим значение у=200, тогда x=0. Масса сплава: 3500-5 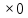 +5 +5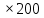 =4500 =4500Ответ: 4500 кг. Задача №11. Фабрика, производящая пищевые полуфабрикаты, выпускает блинчики со следующими видами начинки: ягодная и творожная. В данной ниже таблице приведены себестоимость и отпускная цена, а также производственные возможности фабрики по каждому виду продукта при полной загрузке всех мощностей только данным видом продукта.
|