50 математичесих задач. 50 экономических задач
 Скачать 164.45 Kb. Скачать 164.45 Kb.
|
|
Для выполнения условий ассортиментности, которые предъявляются торговыми сетями, продукции каждого вида должно быть выпущено не менее 15 тонн. Предполагая, что вся продукция фабрики находит спрос (реализуется без остатка), найдите максимально возможную прибыль, которую может получить фабрика от производства блинчиков за 1 месяц Решение Пусть x тонн выпускает фабрика блинчиков с ягодами, а y тонн – с творогом. Тогда по условию имеем : x 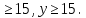 Составим функцию прибыли: ∑(x,y) = 30x+35y→наиб Пусть производственная возможность равна 1, тогда 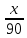 + + 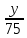 = 1 = 175x + 90y = 6750 x = 90 – 1,2y ∑(y) = 30(90 – 1,2y)+35y→наиб ∑(y) = 2700 - y→наиб Возьмём производную этой функции 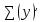 = = 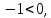 Значит функция убывает во всей области определения, т.е. принимает своё наибольшее значение при y=15. Тогда x = 90-1,2 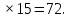 При этом максимальная прибыль будет 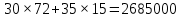 рублей. рублей.Ответ: 2685000 рублей. Задача №12. Консервный завод выпускает фруктовые компоты в двух видах тары — стеклянной и жестяной. Производственные мощности завода позволяют выпускать в день 90 центнеров компотов в стеклянной таре или 80 центнеров в жестяной таре. Для выполнения условий ассортиментности, которые предъявляются торговыми сетями, продукции в каждом из видов тары должно быть выпущено не менее 20 центнеров. В таблице приведены себестоимость и отпускная цена завода за 1 центнер продукции для обоих видов тары.
Предполагая, что вся продукция завода находит спрос (реализуется без остатка), найдите максимально возможную прибыль завода за один день (прибылью называется разница между отпускной стоимостью всей продукции и её себестоимостью). Решение Пусть x центнеров выпускает фабрика в стеклянной таре, а y центнеров – в жестяной. Тогда по условию имеем : x 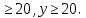 Составим функцию прибыли: ∑(x,y) = 600x+650y→наиб Пусть производственная возможность равна 1, тогда 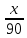 + + 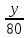 = 1 = 180x + 90y = 7200 x = 90 – 1,125y ∑(y) = 600(90 – 1,125y)+650y→наиб ∑(y) = 54000 - 25y→наиб Возьмём производную этой функции 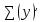 = = 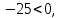 Значит функция убывает во всей области определения, т.е. принимает своё наибольшее значение при y=20. Тогда x = 90-1,12 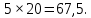 При этом максимальная прибыль будет 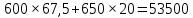 рублей. рублей.Ответ: 53500 рублей. 3.4 Нестандартные задачи Задача №1. Два велосипедиста равномерно движутся по взаимно перпендикулярным дорогам по направлению к перекрестку этих дорог. Один из них движется со скоростью 40 км/ч и находится на расстоянии 5 км от перекрестка, второй движется со скоростью 30 км/ч и находится на расстоянии 3 км от перекрестка. Через сколько минут расстояние между велосипедистами станет наименьшим? Каково будет это наименьшее расстояние? Решение:
Составим функцию квадрата расстояния между велосипедистами: ∑(t) = 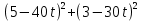 →наим, где t →наим, где t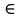 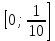 ∑(t) = 25-400t+1600 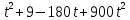 →наим →наим∑(t) = 2500 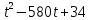 →наим →наимВозьмём производную этой функции 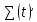 = 5000t-580 = 5000t-580Найдём нули производной: 5000t-580=0 t = 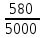 = =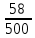 = =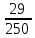 Функция принимает своё наименьшее значение при t= 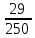 ч = 60 ч = 60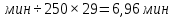 (точка минимума). (точка минимума). Найдём расстояние между велосипедистами: 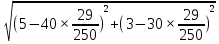 = = 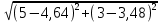 = = 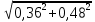 = =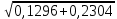 = =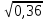 = 0,6 = 0,6Ответ:_0,6км,_6,96_минут_.'>Ответ: 0,6км, 6,96 минут . Задача №2 . Бриллиант массой 20 карат был разбит на две части после чего его стоимость уменьшилась на 25,5%.а) Найдите массы частей на которые был разбит бриллиант если известно, что цена бриллианта пропорциональна квадрату его массы.б) На какое максимальное число процентов может уменьшиться цена бриллианта разбитого на две части. Решение: M=20 карат, S- стоимость бриллианта S=km Пусть m S1+S2=0,745S kx2+k(20-x)2=0,745 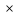 k k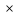 202 202x2+(20-x)2=298 x2+400-40x+102=0 x2-20x+51=0 x1=17, x2=3 Ответ: массы частей 17 и 3 карат. Цена бриллианта максимально снизится, если обе части будут по 10 карат S1+S2=aS k 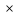 102+k 102+k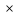 102=a 102=a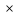 202 202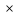 k k100+100=a 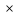 400 400a=200/400=0,5 Ответ: на 50% Задача №3 В одной стране в обращении находились 1000000 долларов, 20% из которых были фальшивыми. Некая нехорошая структура стала ввозить в страну по 100000 долларов в месяц, 10% из которых были фальшивыми. В это время другая структура стала вывозить из страны 50000 долларов ежемесячно, из которых 30% оказались фальшивыми. Через сколько месяцев содержания фальшивых долларов в стране составит 5%? Решение: n - количество месяцев
200000-5000n =0,05(1000000+50000n ) 200000-5000n =50000+2500n -7500n = -150000 n=20 Ответ: 20 месяцев Задача №4 Два брокера купили акции одного достоинства на сумму 3640 рублей. Когда цена на эти акции возросла, они продали часть акций на сумму 3927 рублей. Первый брокер продал 75% своих акций, а второй – 80%. При этом сумма от продажи акций, полученная вторым брокером, на 140% больше суммы первого. На сколько процентов возросла цена одной акции? Решение: k- первоначальная цена 1 акции x – штук купил первый брокер y – штук купил второй z – конечная цена 1 акции Составим систему уравнений: 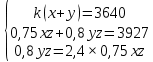 3) 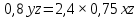 y = 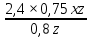 = 2,25x = 2,25xk(x+y)=3640 k(x+2.25x)=3640 k = 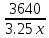 = = 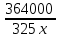 = = 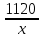 z(0,75x+0,8y)=3927 z(0,75х+1,8x)=3927 z 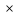 2,55x=3927 2,55x=3927z= 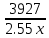 = = 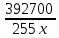 = = 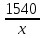 4) Найдём, на сколько процентов возросла цена одной акции k = 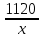 - 100% - 100%z = 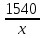 - a% - a%a= 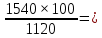 137,5% 137,5%Ответ: на 37,5% Задача №5. Строительство нового завода стоит 115 млн рублей. Затраты на производство x тыс. единиц продукции на таком заводе равны 0,5 x2+x+9 млн рублей в год. Если продукцию завода продать по цене p тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит px-(0,5 x2+x+9). Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении p строительство завода окупится не более чем за 5 лет? Решение Составим функцию прибыли: ∑(x,p) =px-(0,5 x2+x+9)→наиб ∑(x,p) = px-0,5 x2-x-9 Возьмём производную этой функции 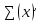 = p-x-1 = p-x-1Найдём нули производной: p-x-1=0 x = p-1 Функция принимает своё наибольшее значение при x = p-1 (точка минимума). Найдём прибыль: ∑(p) = p(p-1)-0,5 (p-1)2-(p-1)-9 = 0,5p2-p-8,5 По условию строительство завода должно окупиться не более, чем за 5 лет. То есть за 5 лет прибыль должна быть не меньше 115 млн рублей. 5(0,5p2-p-8,5 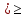 115 1150,5p2-p-8,5-23=0 p2-2p-63=0 p1=9, p2=-7 Ответ: 9 тысяч рублей. 4.Заключение В данной работе рассмотрены основные методы решения задач на кредит, вклады и оптимизацию. Тема работы очень актуальна, так как все рассматриваемые задачи взяты из материалов по подготовке к ЕГЭ по математике «Профиль». Надеюсь, что данная работа будет полезна учащимся 10-11 класса, а также преподавателям математики. 5.Список использованной литературы: 1. ЕГЭ 2018 под редакцией А. Л. Семенова, И.В. Ященко 2. Открытый банк заданий ЕГЭ fipi.ru 3. Сайт «Решу ЕГЭ» 4. Сайт «Алекс Ларин» |
