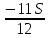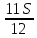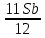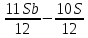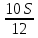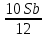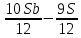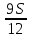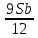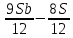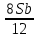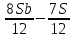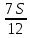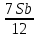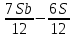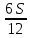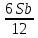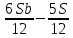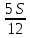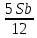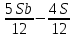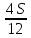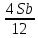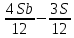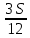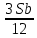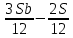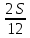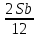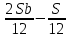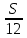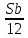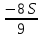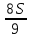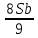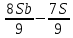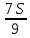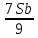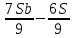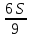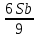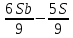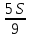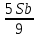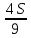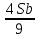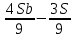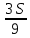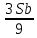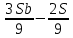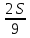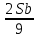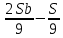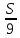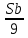50 математичесих задач. 50 экономических задач
 Скачать 164.45 Kb. Скачать 164.45 Kb.
|
|
Ответ: 22,5 процента. Задача №2. 15-го января планируется взять кредит в банке на 1 млн рублей на 6 месяцев. Условия его возврата таковы: − 1-го числа каждого месяца долг возрастает на целое число r процентов по сравнению с концом предыдущего месяца; − со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; − 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей
Найдите наибольшее значение r, при котором общая сумма выплат будет составлять менее 1,2 млн рублей. Решение: S – сумма кредита (1000000рублей) Найти : r% - годовые (ежемесячные) проценты b=1+0,01r – коэффициент
Общая сумма выплат: (Sb+0,6Sb+0,4Sb+0,3Sb+0,2Sb+0,1Sb)-(0,6S+0,4S+0,3S+0,2S+0,1S)= 2,6Sb-1,6S=S(2,6b-1,6)=1*(2,6b-1,6)=2,6b-1,6 2,6b-1,6<1,2 ; 2,6b<2,8 ; b<1,076 ; b=1,07 ; r=7 Ответ: 7 процентов. Задача №3. В июле 2016 года планируется взять кредит в банке в размере S тыс. рублей, где S — натуральное число, на 3 года. Условия его возврата таковы − каждый январь долг увеличивается на 15% по сравнению с концом предыдущего года; − с февраля по июнь каждого года необходимо выплатить одним платежом часть долга; − в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
Найдите наименьшее значение S, при котором каждая из выплат будет составлять целое число тысяч рублей. Решение: S – сумма кредита r% - годовые (ежемесячные) проценты (15%) b=1+0,01r – коэффициент (1,15)
1 выплата 1,15S-0,7S= 0,45S= 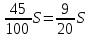 2 выплата 0,7*1,15S-0,4S= 0,405S= 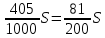 3 выплата 0,4*1,15S= 0,46S= 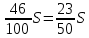 По условию, все выплаты должны быть целыми. Значит, число S должно делиться на 20, 200 и 50. Наименьшее общее кратное этих чисел равно 200. Ответ: 200 тысяч. 7 тип: Задачи, связанные с дифференцированными платежами. Задача №1. Алексей взял кредит в банке на срок 12 месяцев. По договору Алексей должен вернуть кредит ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется r % этой суммы и своим ежемесячным платежом Алексей погашает эти добавленные проценты и уменьшает сумму долга. Ежемесячные платежи подбираются так, чтобы долг уменьшался на одну и ту же величину каждый месяц (на практике такая схема называется «схемой с дифференцированными платежами»). Известно, что общая сумма, выплаченная Алексеем банку за весь срок кредитования, оказалась на 13 % больше, чем сумма, взятая им в кредит. Найдите r. Решение: Сумма кредита (S), ставка (r) -? %, b=1+0,01r
Sb(1+ 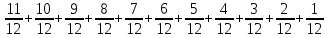 )-S )-S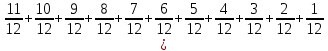 )=1,13S )=1,13S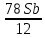 - -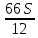 =1,13S /S =1,13S /S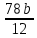 - -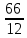 =1,13 =1,1378b=1,13*12+66 b=1,02 r=2% Ответ:2%. Задача 2. 15 января планируется взять кредит в банке на 9 месяцев. Условия его возврата таковы: - 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца; - со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; - 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца. Известно, что на пятый месяц кредитования нужно выплатить 57,5 тыс. рублей. Какую сумму нужно вернуть банку в течение всего срока кредитования? Решение: Сумма кредита (S) Ставка (r) -3 %, b=1,03 n=9 Сумма всех выплат =?
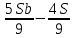 =57,5 =57,55Sb-4S=517,5 S(5b-4)=517,5 S(5*1,03-4)=517,5 S=450 Sb(1+ 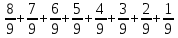 )-S )-S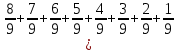 )=5Sb-4S= )=5Sb-4S=450*(5*1,03-4)=450*1,15=517,5 Ответ:517,5 тысяч. Задача 3. 15-го января планируется взять кредит в банке на несколько месяцев. Условия его возврата таковы: — 1-го числа каждого месяца долг возврастает на 5% по сравнению с концом предыдущего месяца; — со 2-го по 14-е число месяца необходимо выплатить часть долга; — 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. На сколько месяцев можно взять кредит, если известно, что общая сумма выплат после полного погашения кредита на 25% больше суммы, взятой в кредит. (решение с помощью формулы суммы арифметической прогрессии) |