8. Решение уравнений и систем 22
 Скачать 1.52 Mb. Скачать 1.52 Mb.
|
8.2. Решение систем уравнений и неравенствMathCAD дает возможность решать также и системы уравнений. Максимальное число уравнений и переменных равно 50. Результатом решения системы будет численное значение искомого корня. Наиболее распространенным является блочный метод. Mathcad решает систему с помощью итерационных методов. Для решения системы этим методом необходимо выполнить следующее: Задать начальное приближение для всех неизвестных, входящих в систему уравнений; Напечатать ключевое слово Given. Оно указывает, что далее следует система уравнений; Введите уравнения и неравенства в любом порядке. Используйте [Ctrl] + = либо палитру, для печати символа =. Между левыми и правыми частями неравенств может стоять любой из символов <, >, и ; Введите любое выражение, которое включает функцию Find, например: 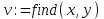 . .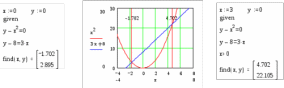 Mathcad возвращает точное решение системы уравнений. Число аргументов должно быть равно числу неизвестных. Решающим блоком – называется часть документа, расположенная между ключевыми словами Given и Find. Внутри блока недопустимы следующие символы: , дискретные переменные или выражения, содержащие дискретный аргумент в любой форме, неравенства вида a Функция, Find может возвращать результат следующими способами: Find (var1, var2,…) =. a: = Find (x) – скаляр, var: = Find (var1, var2,…) – вектор. Удобно при использовании решения системы в другом месте рабочего документа. f (a, b, c, …): = Find (x, y, z, …). Определить другую функцию с помощью Find. Эта конструкция удобна для многократного решения системы уравнений для различных значений некоторых параметров a, b, c,…, непосредственно входящих в систему уравнений; f (x, y, z, …): = Find (x, y, z, …). Если необходимо найти решение при различных начальных приближениях, имеет смысл определить новую функцию.  Последние два способа можно комбинировать. Отсутствие сходимости решения Сообщение об ошибке 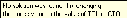 (Решение не найдено) при решении уравнений появляется, когда: (Решение не найдено) при решении уравнений появляется, когда:система не имеет решения; для уравнения, которое не имеет вещественных решений, в качестве начального приближения взято вещественное число и наоборот; в процессе поиска решения последовательность приближений попала в точку локального минимума невязки. Для поиска искомого решения нужно задать различные начальные приближения; возможно, поставленная задача не может быть решена с заданной точностью. Попробуйте увеличить значение TOL. Приближенные решения Функция Minerr очень похожа на функцию Find (использует тот же алгоритм). Если в результате поиска не может быть получено дальнейшее уточнение текущего приближения к решению, Minerr возвращает это приближение. Функция Find в этом случае возвращает сообщение об ошибке. Правила использования функции Minerr такие же, как и функции Find. Общий вид Minerr Minerr (z1, z2,.). Число аргументов должно быть равно числу неизвестных. При использовании Minerr используется в блоке решения уравнений, необходимо всегда включать дополнительную проверку достоверности результатов.  Решение матричных уравнений Система n линейных алгебраических уравнений относительно n неизвестных х1, х2, …, хn может быть записана в матричном видеах=b где: 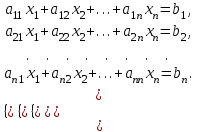 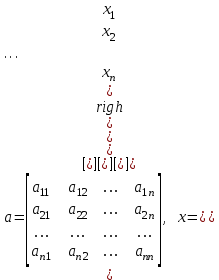 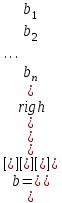 . .Если матрица а – неособенная, то есть det (а) 0 то система, имеет единственное решение. Для решения систем линейных уравнений можно использовать общепринятые математические методы: метод Крамера, матричный метод и т.д. Системы линейных уравнений удобно решать с помощью функции lsolve (а, b) – где а – матрица коэффициентов (не сингулярная), b – вектор свободных членов.  8.3. Решение дифференциальных уравнений и системОсновные функции Для решения дифференциальных однородных дифференциальных уравнений (ОДУ) – 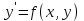 с начальными условиями с начальными условиями 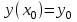 пакет Mathcad имеет ряд встроенных функций: пакет Mathcad имеет ряд встроенных функций:rkfixed – функция решения ОДУ и систем ОДУ методом Рунге-Кутта четвертого порядка с постоянным шагом; Rkadapt – функция решения ОДУ и систем ОДУ методом Рунге-Кутта с переменным шагом; Bulstoer – функция решения ОДУ и систем ОДУ методом – метод Булирша-Штёра если заранее известно, что решением является гладкая функция. Рассмотрим подробнее каждую из этих функций: rkfixed (y, x1, x2, p, D) – возвращает матрицу первый столбец которой содержит точки, в которых получено решение, а остальные столбцы – решения, первые n-1 производные. Функция возвращает матрицу, состоящую из 1+n строк. Аргументы функции: y – вектор начальных условий (k элементов); x1 и x2 – границы интервала, на котором ищется решение ОДУ; p – число точек внутри интервала (x1, x2), в которых ищется решение; D – вектор, состоящий из k элементов, который содержит первые производные искомой функции. Rkadapt (y, x1, x2, p, D) – назначение параметров то же, что и для функции rkfixed. Существует несколько модифицированная функция rkadapt (y,x1,x2, acc,p,D,k,s) – где добавлены параметры k – максимальное число промежуточных точек решения; s – минимально допустимый интервал между точками; acc – погрешность решения (рекомендуется порядка 0.001). Bulstoer (y, x1, x2, p, D) – назначение параметров то же, что и для функции rkfixed. Рекомендации по использованию Обычно функция Rkadapt благодаря автоматическому изменению шага решения дает более точный результат, но по скорости вычислений она проигрывает функции rkfixed, хотя если решение меняется медленно, она может привести к заметному уменьшению числа вычислений. Поэтому функция Rkadapt наиболее пригодна для решения ОДУ дающих медленно меняющееся решения. Примеры решения дифференциальных уравнений 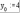 1. Решим ОДУ 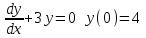 . .2. Задаем вектор начальных условий: 3 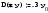 . Задаем вектор – функцию первой производной неизвестной функции: Д 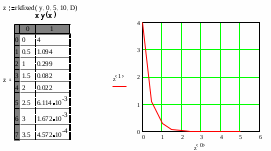 ля решения воспользуемся функцией rkfixed: Решим дифференциальное уравнение второго порядка: 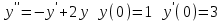 . .Преобразуем уравнение в систему ОДУ первого порядка, решенных относительно первой производной: 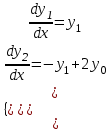 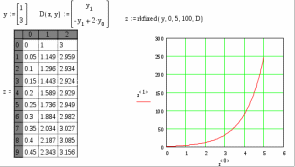 Решим систему линейных уравнений первого порядка: 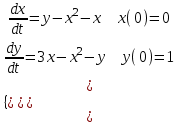 . .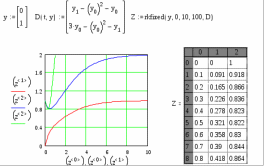 4. Решим систему двух линейных уравнений второго порядка: 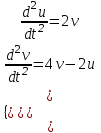 с начальными условиями с начальными условиями 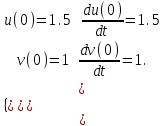 . .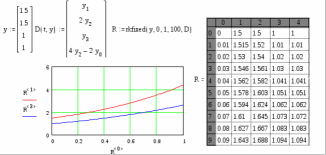 |
