8. Решение уравнений и систем 22
 Скачать 1.52 Mb. Скачать 1.52 Mb.
|
9. Апроксимация функцийАппроксимацией (приближением) функции 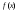 называется нахождение такой функции называется нахождение такой функции 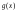 (аппроксимирующей функции), которая была бы близка заданной. Критерии близости функций (аппроксимирующей функции), которая была бы близка заданной. Критерии близости функций 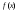 и и 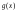 могут быть различные. могут быть различные.В том случае, когда приближение строится на дискретном наборе точек, аппроксимацию называют точечной или дискретной. В том случае, когда аппроксимация проводится на непрерывном множестве точек (отрезке), аппроксимация называется непрерывной или интегральной. Примером такой аппроксимации может служить разложение функции в ряд Тейлора, то есть замена некоторой функции степенным многочленом. Наиболее часто встречающим видом точечной аппроксимации является интерполяция (в широком смысле). В том случае, когда полином един для всей области интерполяции, говорят, что интерполяция глобальная. В тех случаях, когда между различными узлами полиномы различны, говорят о кусочной или локальной интерполяции. Найдя интерполяционный полином, мы можем вычислить значения функции 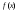 между узлами (провести интерполяцию в узком смысле слова), а также определить значение функции между узлами (провести интерполяцию в узком смысле слова), а также определить значение функции 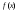 даже за пределами заданного интервала (провести экстраполяцию). даже за пределами заданного интервала (провести экстраполяцию).Следует иметь в виду, что точность экстраполяции обычно очень невелика. 10. Регрессия функцийРегрессия – представление совокупности данных некоторой функцией f (x). Задачей регрессии является вычисление параметров функции f (x) таким образом, чтобы функция приближала "облако" исходных точек с наименьшей погрешностью. При этом функция f (x) называется уравнением регрессии. При регрессии не требуется чтобы функция проходила через все заданные точки, что особенно важно при аппроксимации данных, заведомо содержащих ошибки. Линейная регрессия Линейная регрессия является простейшим видом регрессии. Классическим алгоритмом линейной регрессии является метод наименьших квадратов. В котором критерием является минимизация суммы квадратов отклонений аппроксимирующей функции от заданных точек: 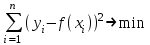 . .Существуют и другие алгоритмы определения коэффициентов линейной регрессии – метод медиан. В общем виде аппроксимирующею функцию можно представить как 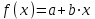 . Задачей линейной регрессии является вычисление параметров a и b. Для этого в MathCad существует ряд встроенных функций (где VX, VY – вектора узловых точек): . Задачей линейной регрессии является вычисление параметров a и b. Для этого в MathCad существует ряд встроенных функций (где VX, VY – вектора узловых точек):corr (VX, VY) – возврящает скаляр – коэффициент корреляции Пирсона. Чем ближе коэффициент к 1 тем точнее исходная зависимость приближается к линейной; intercept (VX, VY) – возвращает значение параметра а (свободный член) рассчитанного методом наименьших квадратов; slope (VX, VY) – определяет значение параметра b (угловой коэффициент) рассчитанного методом наименьших квадратов; line (VX, VY) – [MathCAD 2000] возвращает вектор первый элемент которого параметр а, второй b рассчитанные по методу наименьших квадратов; medfit (VX, VY) – [MathCAD 2000] возвращает вектор первый элемент которого параметр а, второй b рассчитанные по методу медиан. Как видно из примера при аппроксимации линейной регрессией прямая проходит через "облако" точек.  Используя встроенные функции можно рассчитывать регрессию не только для линейных, но и для экспоненциальных функций 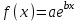 . Для этого f (x) с помощью логарифмирования по натуральному основанию приводится к линейной. Рассчитанный коэффициент а, полученный в логарифмической форме, затем пересчитывается. . Для этого f (x) с помощью логарифмирования по натуральному основанию приводится к линейной. Рассчитанный коэффициент а, полученный в логарифмической форме, затем пересчитывается.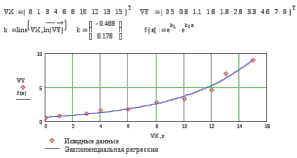 Линейная регрессия общего вида MathCAD позволяет проводить линейную регрессию общего вида, в которой аппроксимирующая функция задается линейной комбинацией функций, причем сами фикции fi (x) могут быть не линейными: 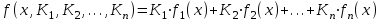 . .Линейная регрессия общего вида реализуется с помощью функции linfit (VX, VY,F) – возвращающей вектор коэффициентов К, при котором среднеквадратичная погрешность приближения "облака" исходных точек с координатами VX, VY, минимальна. Вектор F содержит функции fi (x) записанные в символьном виде. Вектор VX должен быть возрастающим. 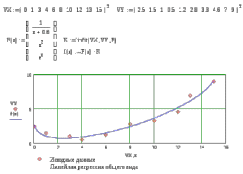 Полиномиальная регрессия Полиномиальная регрессия позволяет аппроксимировать зависимость полиномом произвольной степени. Вычисление коэффициентов полинома осуществляется с помощью встроенной функции regress (VX, VY,n), где VX, VY – вектора с координатами исходных данных, n – порядок полинома (первые три возвращаемые коэффициенты служебные, а далее искомые значения расположенные по возрастанию степени полинома). Для построения аппроксимирующей зависимости можно воспользоваться либо встроенной функцией interp (VK,VX, VY,x), либо функцией 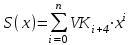 , где VK – вектор коэффициентов расчитанных функцией regress; x – рассчитываемая точка. Для проведения регрессии необходимо что бы вектор VX был возрастающим и его количество его элементов было больше степени полинома на 1. , где VK – вектор коэффициентов расчитанных функцией regress; x – рассчитываемая точка. Для проведения регрессии необходимо что бы вектор VX был возрастающим и его количество его элементов было больше степени полинома на 1.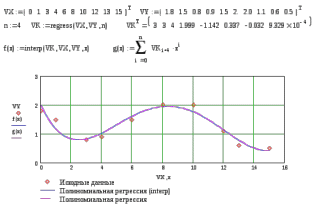 Функция regress определяет единственный приближающий полином, элементы которого вычисляются по всей совокупности точек. Для проведения локальной регрессии используется функция loess (VX, VY,span) – дающая приближение отрезками полиномов второй степени, где span – величина задающая длину отрезков. Чем больше величина span>0, тем сильнее сглаживаются данные. Чем меньше шаг между точками VX, тем меньше должно быть span. При больших значениях span функция приближается к regress (VX, VY,2). Рекомендуемое значение 0.75, однако оно подходит далеко не всегда и требует уточнения. 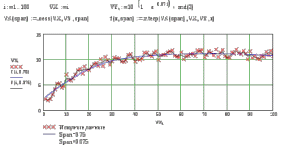 Нелинейная регрессия общего вида Для выполнения нелинейной регрессии общего вида необходимо определить параметры произвольной аппроксимирующей функции 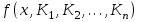 , при которой обеспечивается минимальная среднеквадратичная ошибка. Для этого используется встроенная функция genfit (VX,VY,VS,F) – которая возвращает вектор K параметров функции , при которой обеспечивается минимальная среднеквадратичная ошибка. Для этого используется встроенная функция genfit (VX,VY,VS,F) – которая возвращает вектор K параметров функции 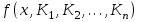 . Вектор VS – задает начальные приближения элементов вектора K рассчитываемых итерационным способом, вектор F содержит искомую функцию и ее частные производные по параметрам Ki в аналитическом виде: . Вектор VS – задает начальные приближения элементов вектора K рассчитываемых итерационным способом, вектор F содержит искомую функцию и ее частные производные по параметрам Ki в аналитическом виде: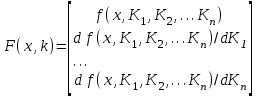 . .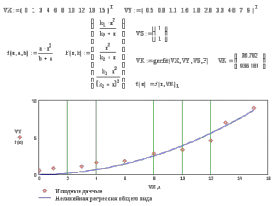 11. Интерполирование функцийИнтерполирование – способ приближенного или точного нахождения, какой либо величины по известным отдельным значениям, её или других величин, связанных с ней. Задача интерполирования состоит в том, чтобы подобрать многочлен f (x) с действительными коэффициентами проходящий через все узлы интерполяции yi. Критерием близости функции является 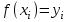 . Дискретный набор значений . Дискретный набор значений 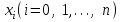 – называют узлами интерполяции, а многочлен f (x) интерполяционным полиномом. Для выполнения интерполяции средствами MathCAD необходимо, что бы точки xi были возрастающими и не совпадающими, а также были заданы значения yi для всех точек. – называют узлами интерполяции, а многочлен f (x) интерполяционным полиномом. Для выполнения интерполяции средствами MathCAD необходимо, что бы точки xi были возрастающими и не совпадающими, а также были заданы значения yi для всех точек.Кусочная линейная интерполяция Кусочная линейная интерполяция является простейшим случаем локальной. Интерполяционной функцией является полином первой степени, то есть узловые точки соединяются прямой. Линейная интерполяция осуществляется с помощью встроенной функции linterp (VX,VY,x), где VX, VY – вектора узловых точек; x – рассчитываемая точка. 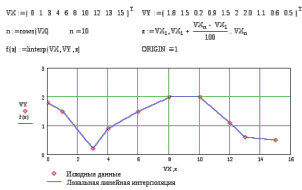 Сплайновая интерполяция Среди методов локальной интерполяции наибольшее распространение получила интерполяция сплайнами (от англ. spline – гибкая линейка). Идея сплайн – интерполяции в том, что полином высокой степени проходящий через все опорные точки заменяется фрагментами полиномов малых порядков. В MathCAD используются кубические полиномы. При таком способе приближения не появляется множества не связанных со значениями узловых точек экстремумов, и аппроксимирующая функция точно проходит через все узлы и имеет непрерывную первую и вторую производные. На каждом интервале 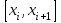 интерполирующую функцию можно представить как полином 3-ей степени интерполирующую функцию можно представить как полином 3-ей степени 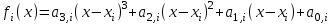 удовлетворяющий условию удовлетворяющий условию 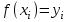 . Коэффициенты полиномов . Коэффициенты полиномов 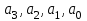 рассчитываются из условия непрерывности первой и второй производных. рассчитываются из условия непрерывности первой и второй производных.2. Практическая частьЗадание 3. Работа с MS Excell 3.1. Составить формулы и просчитать при заданных параметрах. Отформатировать область вычислений по своему усмотрению. Все вычисленные значения должны содержать три знака после запятой. G=500 S=G/120+7 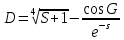 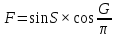   3.2. Используя автозаполнение, выполнить следующее задание и построить график функции Y. Выполните подписи осей и самого графика. 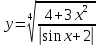 , xизменяется на отрезе [-3;3] с шагом 0,5 , xизменяется на отрезе [-3;3] с шагом 0,5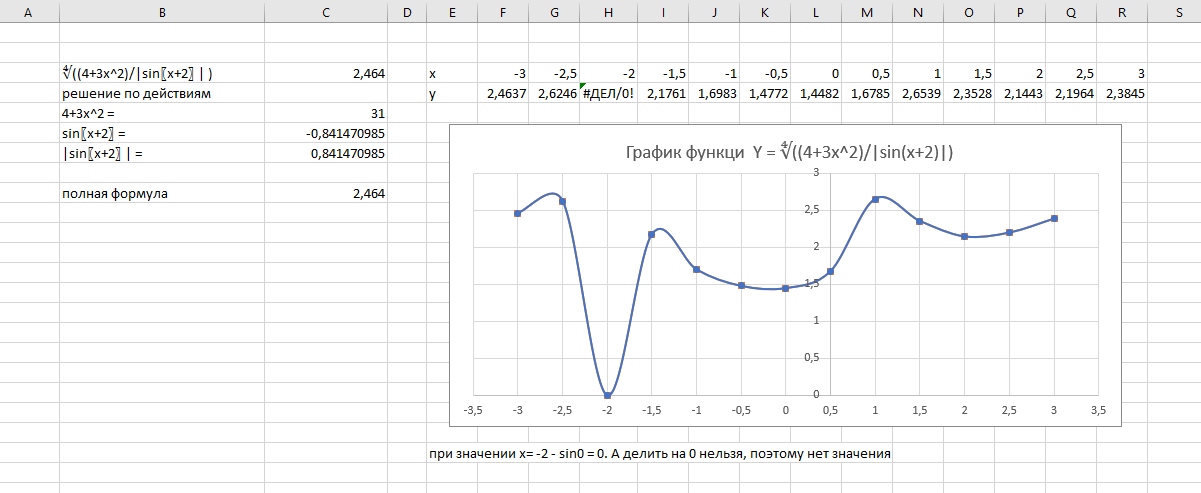 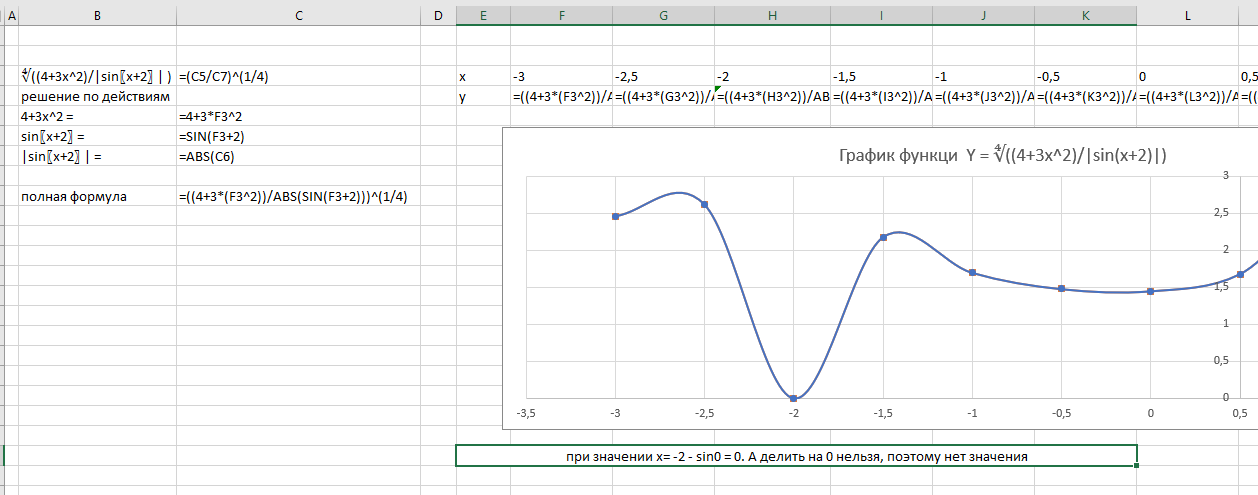 3.3. Постройте расчетную таблицу в соответствии с заданием 1. Создайте рабочую таблицу «Прайс-лист по принтерам» 2. В столбце А в произвольном порядке записать наименования принтеров (точечно-матричные, струйные, лазерные). В столбце В модели принтеров (Epson, HP, Samsung, Olivetti) не менее 5 каждой модели. 3.В столбце С - цену принтеров в любых денежных единицах 4. Построить диаграмму любого типа для каждой модели принтера 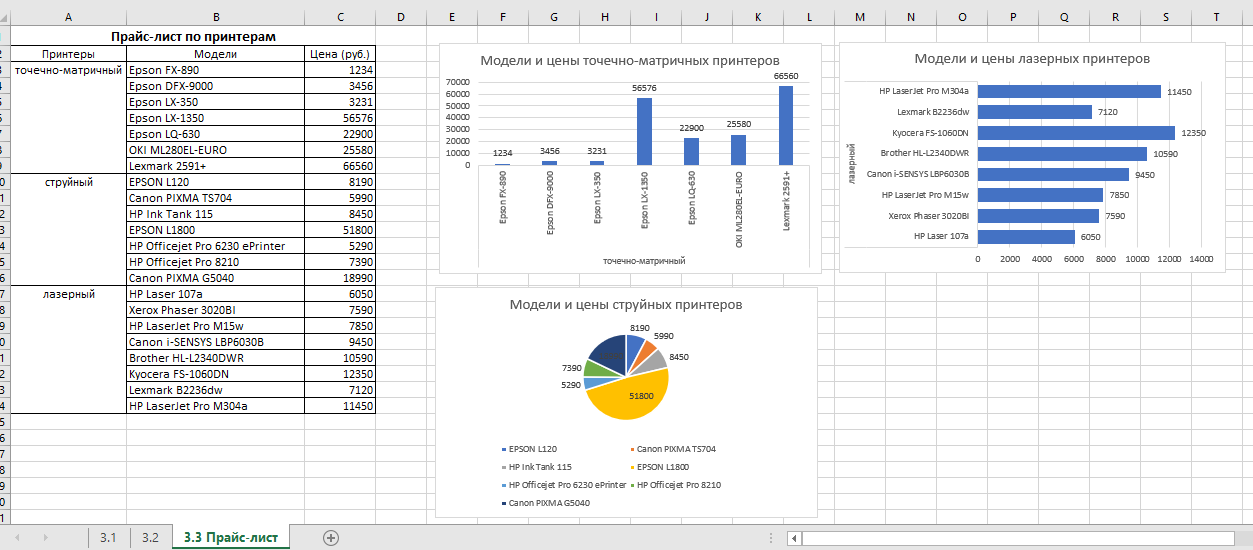 Список использованной литературыMathCAD. Среда. Методы решения задач: методическое пособие / С. Н. Гуз, С. Н. Дегтяр. - Мозырь: МГПУ, 2012. - 102 с. Кирьянов, Д. В. Самоучитель MathCAD.-СПб.: БХВ-Петербург, 2003.-560 с. Плис, А.И. MathCAD: Математический практикум для экономистов и инженеров/ А. И. Плис, Н. А. Сливина. - М.: Финансы и статистика, 2010. - 656 с. Поршнев, С.В. Компьютерное моделирование физических систем с использованием пакета MathCAD: Учебное пособие / С.В. Поршнев. - М.: Горячая линия - Телеком, 2015. - 320 c. ПриложенияЗадание №2. Изменение содержания колонтитулов 1. верхний колонтитул 1 листа должен содержать фамилию и инициалы, остальные - отражать заголовки рассматриваемых пунктов 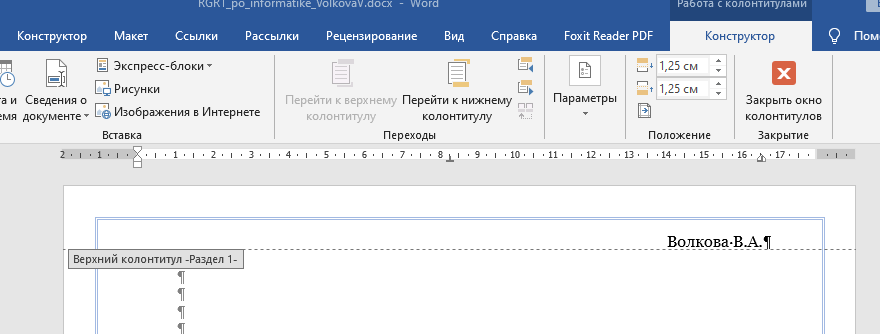 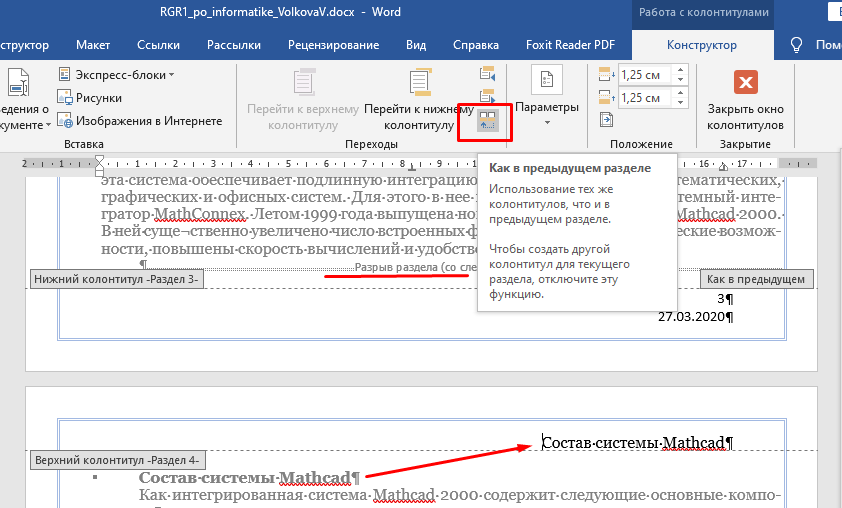 1.2. Нижний колонтитул должен содержать номер страницы и дату создания документа 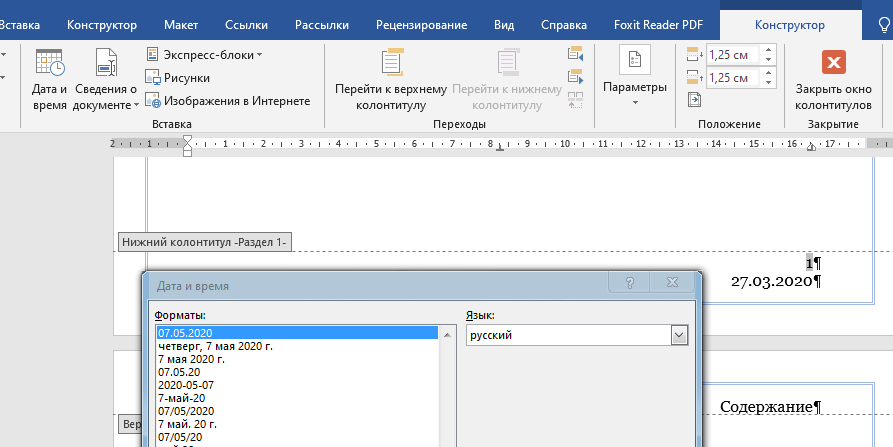 Отформатируйте текст в соответствии с требованиями: Шрифт Georgia 12 pt 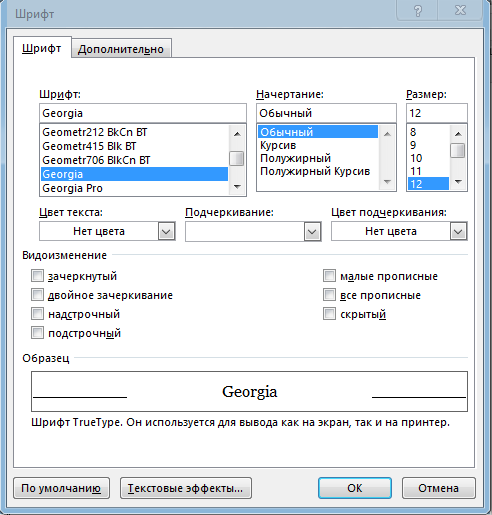 Вырывание по ширине, первая строка отступ 1 см, межстрочный интервал – множитель=0,95 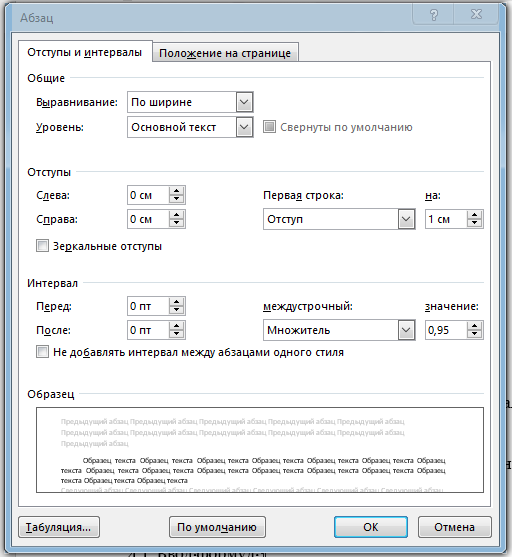 Поля: верхнее, нижнее, правое – 1 см, левое – 2 см 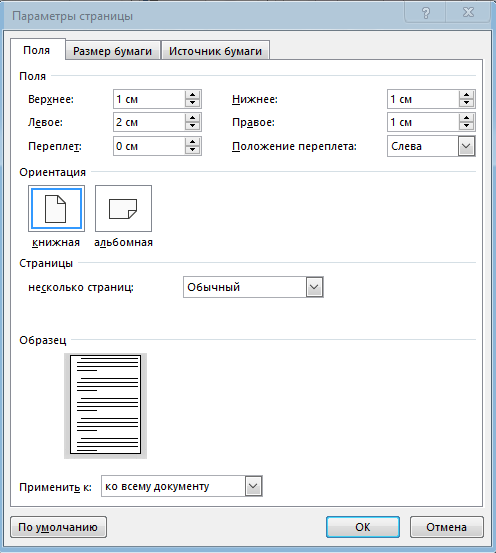 Расстановка переносов - Авто 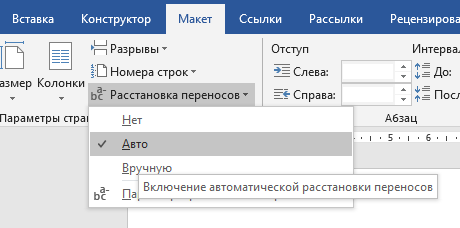 Вставьте двойную рамку вокруг страницы – синего цвета 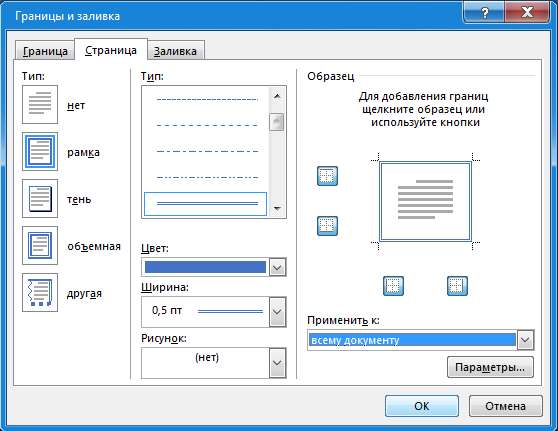 Создайте оглавление  27.03.2020 |
