8. Решение уравнений и систем 22

• Название: 8. Решение уравнений и систем 22
• Дата: 20.11.2021
• Размер: 1.52 Mb.
• Имя файла: RGR_po_informatike_ispr.docx
• Тип: Реферат; #277453
• страница: 4 из 9

5. Формат вывода числовых данных

При работе с вычислительными областями с помощью команды Format – Number, возможно установить формат вывода числовых данных. Это окно содержит три выделенные части В первой – Radix – устанавливается тип основания чисел Decimal, Hex или Octal.

Вторая часть Precision (точность) – задает погрешность вычислений в виде показателя степени n для числа 10 в этой степени. Задаются число отображаемых знаков Displayed (точность вывода), границы представления чисел в экспоненциальной форме Exponential Threshold (диапазон показателя), допустимая граница для комплексных чисел Complex Tolerance (комплексная точность) и допустимая граница для действительных чисел Zero Tolerance (точность нуля).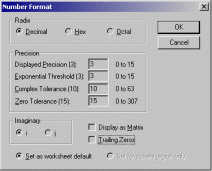


Окно для установки формата чисел
В третьей части – Imaginary (мнимая единица) – задается знак мнимой единицы для комплексных чисел i или j. Если Re (Z) /Im (Z) >10n, то комплексное число Z выводится как действительное, а если Im (Z) /Re (Z) >10ⁿ, то число Z выводится как мнимое. Значения n для этих представлений задает параметр Complex Tolerance. Если действительное число больше числа 10 в степени п или меньше, чем 10 в степени – n, где n – значение параметра Exponencial Threshold, то число представляется в экспоненциальной форме. Если значения чисел по модулю меньше указанных параметром Zero Tolerance, числа представляются в виде нулей. Все это особенно важно при научно-технических расчетах, когда излишняя точность представления чисел ни к чему хорошему не ведет

С помощью диалогового окна можно сделать формат глобальным (Global) или локальным (Local). Глобальный формат задает представление для всех числовых данных документа, а локальный – только для текучего блока.

Для массивов чисел их вывод задается в виде матрицы – включением опции Display as Matrix (отображение в виде матрицы). Однако для больших массивов это может быть неприемлемо, так как такая матрица выходит за пределы экрана. Если опция отключена, то большие массивы отображаются как электронные таблицы. Trailig Zeros – включает отображение нулевых младших разрядов.

6. Структурированные данные

1. Дискретные переменные

Дискретной называется переменная, содержащая несколько значений, каждое из которых отличается от предыдущего на величину постоянного шага и имеющая начальное и конечное значение. Эти переменные имеют два способа определения:

Name: = Nbegin. Nend;

Name: = Nbegin, (Nbegin + Step). Nend.

где Name – имя переменной, Nbegin – ее начальное значение,Nend – конечное значение,. (; на клавиатуре, либо m. n – в арифметической палитре) – символ, указывающий на изменение переменной в заданных пределах (вводится клавишей;). Step – шаг изменения переменной (он должен быть положительным, если Nbegin< Nend, или отрицательным в обратном случае).

Если шаг не указывается (1 способ), то он выбирается равным единице. Если Nbegin< Nend, то шаг переменной будет равен +1, иначе – 1.

Дискретные аргументы значительно расширяют возможности MathCAD, позволяя выполнять многократные вычисления или циклы с повторяющимися вычислениями, формировать векторы и матрицы. Параметрами могут быть константы, переменные, выражения.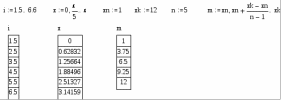

Функция дискретного аргумента имеет множество значений, каждое из которых соответствует соответствующему значению дискретного аргумента. Дискретная переменная может являться аргументом функции пользователя или индексом для организации одномерных и двумерных массивов.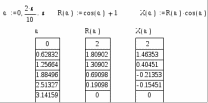

2. Векторы и массивы

Массив – имеющая уникальное имя совокупность конечного числа числовых или символьных элементов, упорядоченных некоторым образом и имеющих определенные адреса. В пакете MathCAD используются массивы двух наиболее распространенных типов: одномерные (векторы), двумерные (матрицы).

Порядковый номер элемента, который является его адресом, называется индексом. Индексы могут иметь только целочисленные значения. Они могут начинаться с нуля или другого целого числа, в соответствии со значением системной переменной ORIGIN. Значение этой переменной может быть переопределено непосредственно в документе, либо с помощью меню Math-Options.

1. векторы и матрицы можно задавать различными способами: с помощью команды Insert – Matrix, комбинации клавиш Ctrl + M, щелчком на кнопке панели Matrix. В появившемся окне задают размерность массива (Columns – столбцы, Rows – строки). Пустые поля заполняют, перемещаясь между ними клавишей Tab. Максимальный размер вводимых таким способом матриц – 10х10, поэтому большие матрицы задают с помощью компоненты Insert – Component – Input Table. Данный компонент вставляет в рабочий документ лист электронной таблицы (подобный листу в Excel). При таком способе ввода матрицы не существует ограничений на ее размер, а использование функций табличного процессора облегчает ввод и просмотр больших массивов, целиком не помещающихся в рабочей области;

2. как переменные с индексами (номер элемента в массиве). Нижний индекс вводится нажатием клавиши [, либо щелчком на кнопке X_n панели Arithmetic. Незаданные элементы по умолчанию задаются нулевыми.;

3. как переменная с индексом, а элементы в массив заносятся перечислением, через запятую;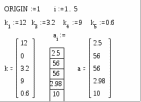


4. с использованием дискретного аргумента, когда имеется некоторая явная зависимость для вычисления элементов массива через их индексы.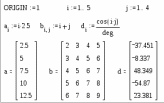

Для удобства отображения, громоздкие массивы выводятся в виде электронной таблицы с номерами строк и столбцов и полосами прокрутки. Формат представления данных в таблицах может быть изменен с помощью команды Format-Number – Display as Matrix.
3. Обращение к элементам массива

Массивы могут использоваться в выражениях целиком или поэлементно. Для обращения к элементам массивов нужно указать числовые значения индексов элементов. Также можно обращаться к конкретной строке или столбцу матрицы с помощью верхнего индекса (выделения столбца CTRL+^) или нижних индексов.

4. Параллельные вычисления, векторизация.

Большинство вычислений с дискретными переменными и массивами строятся на принципе параллельных (поэлементных) вычислений. Точно такая же операция может быть выполнена с помощью векторизации. Векторизация – проведение некоторой операции над всеми элементами вектора или матрицы.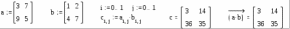


Операция векторизации позволяет применить математические операции и функции к каждому элементу массива поочередно. Система позволяет выполнять рекуррентные вычисления, когда последующий элемент массива вычисляется через предыдущий по какому либо закону.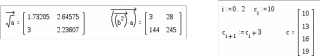