8. Решение уравнений и систем 22
 Скачать 1.52 Mb. Скачать 1.52 Mb.
|
7. Стандартные и пользовательские функцииФункция – выражение, согласно которому проводятся некоторые вычисления с аргументами и определяется её числовое значение. С 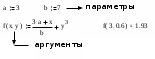 ледует особо отметить разницу между аргументами и параметрами функции. Переменные, указанные в скобках после имени функции, являются ее аргументами и заменяются при вычислении функции значениями из скобок. Переменные в правой части определения функции, не указанные скобках в левой части, являются параметрами и должны задаваться до определения функции. Главным признаком функции является возврат значения, т.е. функция в ответ на обращение к ней по имени с указанием ее аргументов должна возвратить свое значение. Функции в пакете MathCAD могут быть встроенные (cos, sin, ln), т.е. заблаговременно введенные разработчиками, и определенные пользователем. Способы вставки встроенной функции: Выбрать пункт меню Insert – Function. Нажать комбинацию клавиш Ctrl + F. Щелкнуть на кнопке  . .Пакет MathCAD позволяет расширить систему новыми функциями представляющими интерес для пользователя. Функция пользователя в общем случае имеет вид: Имя_функции (Список аргументов): =Выражение. Имя функции задается как любой идентификатор. Список аргументов функции разделяется запятыми. Аргументы функции являются локальными для неё переменными, поэтому они могут, не определятся до задания функции. Локальные переменные действуют только в выражении, описывающем функцию. При этом их имена могут совпадать с именами глобальных переменных, но при выходе из блока функции значения этих переменных сохраняют ранее заданные значения. Функции пользователя также могут описываться как локальные, так и глобальные. К сожалению, функции пользователя нельзя применять в составе выражений, над которыми осуществляются символьные операции. Стандартные функции Классификация стандартных функций Пакет MathCAD является мощной вычислительной системой за счет наличия огромного количества стандартных функций, которые можно классифицировать следующим образом: математические (арифметические, тригонометрические, гиперболические, комплексные, специальные); векторные и матричные (создания, объединения, работы со строками и столбцами, матричная алгебра, специальные функции); статистические (вероятности, гистограммные, распределения); аппроксимация и интерполяция (интерполяция, аппроксимация, регрессия, сплайны, линейное предсказание); решение линейных, нелинейных, дифференциальных уравнений и систем; доступа к внешним данным (ввод/вывод структурированных и неструктурированных файлов). 7.1. Основные элементарные математические функцииОсновные элементарные математические функции можно разделить на 6 групп: тригонометрические – sin (z), cos (z), tan (z), cot (z), csc (z), sec (z); гиперболические – sinh (z), cosh (z), tanh (z), coth (z), csch (z), sech (z); обратные – asin (z), acos (z), atan (z); обратные гиперболические – asinh (z), acosh (z), atanh (z); показательные и логарифмические – exp (z), ln (z), log (z); функции комплексного аргумента – Re (z), Im (z), arg (z), CTRL+"-комплексно сопряженное. 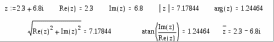 Во всех тригонометрических функция аргумент (z) должен быть в радианах, скалярным и безразмерным. Для перевода из градусов в радианы и обратно удобно использовать встроенную переменную deg. Обратные тригонометрические функции возвращают результат в радианах. 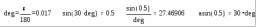 7.2. Основные функции работы с векторами и матрицамиСуществует ряд встроенных векторных и матричных функций. Рассмотрим основные, введя следующие обозначения: V – для векторов, M – для матриц.
|
