8. Решение уравнений и систем 22
 Скачать 1.52 Mb. Скачать 1.52 Mb.
|
8. Решение уравнений и системКак известно, многие уравнения и системы уравнений не имеют аналитических решений. В первую очередь это относится к большинству трансцендентных уравнений. Доказано также, что нельзя построить формулу, по которой можно было бы решить произвольное алгебраическое уравнение степени выше четвертой. Однако такие уравнения могут решаться численными методами с заданной точностью (не более значения заданного системной переменной TOL). 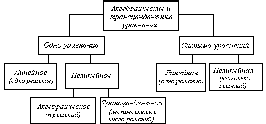 Рис 1. Классификация уравнений Выбор подходящего метода для решения уравнений зависит от характера рассматриваемой задачи. Задачи, сводящиеся к решению алгебраических и трансцендентных уравнений, можно классифицировать по числу уравнений и в зависимости от предлагаемого характера и числа решений. Одно уравнение будем называть линейным, алгебраическимили трансцендентным в зависимости от того, имеет ли оно одно решение, n решений или неопределенное число решений. 8.1. Решение линейных и трансцендентных уравненийДля простейших уравнений вида f (x) =0 решение в MathCad находится с помощью функции root. root (f (х1, x2, …), х1), где f (х1, x2, …) – функция описывающая левую часть выражения вида f (x) =0. Выражение должно возвращать скалярные значения; х1 – имя переменной, относительно которой решается уравнение. Функция реализует вычисления итерационными методами и требует предварительного задания начального приближения искомой переменной (х1). Эта переменная называется варьируемой. Функция позволяет найти как вещественные корни, так и комплексные. В этом случае начальное приближение нужно задать как комплексное число. Приближенные значения корней (начальные приближения) могут быть: Известны из физического смысла задачи; Известны из решения аналогичной задачи при других исходных данных; Найдены графическим способом. Наиболее распространен графический способ определения начальных приближений. В этом случае достаточно построить график функции f (x) и отметить точки пересечения f (x) с осью Ох, или отметить на оси Ох отрезки, содержащие по одному корню. Построение графиков часто удается сильно упростить, заменив уравнение f (x) = 0 равносильным ему уравнением 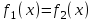 , где функции f1 (x) и f2 (x) – более простые, чем функция f (x). Тогда, построив графики функций у = f1 (x) и у = f2 (x), искомые корни получим как абсциссы точек пересечения этих графиков. Для решения уравнений вида , где функции f1 (x) и f2 (x) – более простые, чем функция f (x). Тогда, построив графики функций у = f1 (x) и у = f2 (x), искомые корни получим как абсциссы точек пересечения этих графиков. Для решения уравнений вида 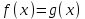 его необходимо привести к виду его необходимо привести к виду 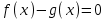 . .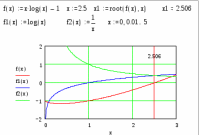 Часто возникает необходимость многократного решения уравнения при изменении одного из параметров. 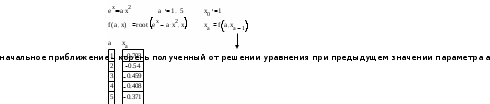 Отсутствие сходимости функции root Если после многих итераций Mathcad не находит подходящего приближения, то появится сообщение 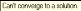 (отсутствует сходимость). Эта ошибка может быть вызвана следующими причинами: (отсутствует сходимость). Эта ошибка может быть вызвана следующими причинами:Уравнение не имеет корней. Корни уравнения расположены далеко от начального приближения. Выражение имеет локальные maxи min между начальным приближением и корнями. Выражение имеет разрывы между начальными приближениями и корнями. Выражение имеет комплексный корень, но начальное приближение было вещественным. Чтобы установить причину ошибки, исследуйте график f (x).Он поможет выяснить наличие корней уравнения f (x) = 0 и, если они есть, то определить приблизительно их значения. Чем точнее выбрано начальное приближение корня, тем быстрее будет rootсходиться. Рекомендации по использованию функции root Для изменения точности, с которой функцияroot ищет корень, нужно изменить значение системной переменной TOL. Если значение TOL увеличивается, функция root будет сходиться быстрее, но ответ будет менее точен. Если значение TOL уменьшается, то функция rootбудет сходиться медленнее, но ответ будет более точен. Значение TOL можно определить непосредственно в рабочем документе, либо в меню Math – Option. Если два корня расположены близко друг от друга, следует уменьшить TOL, чтобы различить их. Если функция f (x) имеет малый наклон около искомого корня, функцияroot (f (x), x) может сходиться к значению, отстоящему от корня достаточно далеко. В таких случаях для нахождения более точного значения корня необходимо уменьшить значение TOL. Другой вариант заключается в замене уравнения f (x) = 0на g (x) = 0 где 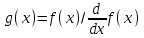 . .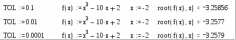 Для выражения f (x) с известным корнем (а) нахождение дополнительных корней f (x) эквивалентно поиску корней уравнения h (x) =f (x) / (x‑a). Подобный прием полезен для нахождения корней, расположенных близко друг к другу. Проще искать корень выражения h (x), чем пробовать искать другой корень уравнения f (x) = 0, выбирая различные начальные приближения. Нахождение корней полинома Для нахождения корней выражения, вида 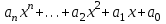 используется функция polyroots. В отличие от функции root, polyrootsне требует начального приближения и возвращает сразу все корни, как вещественные, так и комплексные. Общий вид polyroots (v), где v – вектор коэффициентов полинома длины используется функция polyroots. В отличие от функции root, polyrootsне требует начального приближения и возвращает сразу все корни, как вещественные, так и комплексные. Общий вид polyroots (v), где v – вектор коэффициентов полинома длины 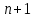 , n – степень полинома. Возвращает вектор длины n, состоящий из корней полинома. Вектор vудобно создавать использую команду меню Symbolics – Polynomial Cofficients. , n – степень полинома. Возвращает вектор длины n, состоящий из корней полинома. Вектор vудобно создавать использую команду меню Symbolics – Polynomial Cofficients.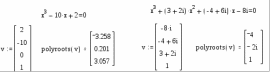 |
