Задачи с параметрами в курсе основной школы. #Задачи с параметрами в курсе основной школы. Александры Анатольевны
 Скачать 1.31 Mb. Скачать 1.31 Mb.
|
B       0 y = ax (a0) x y = x y = –x При a –1 уравнение имеет один корень: x = 0. При a = 1 прямая y = ax (y = x) содержит луч OA, и уравнение имеет бесконечно много корней: x 0. При a = –1 прямая y = ax (y = –x) содержит луч OB, и уравнение имеет беско-нечно много корней: x 0. Графический способ (2). Данное уравнение для любого значения параметра a всегда имеет, по крайней мере, одно решение x = 0, т.к. графики функций y = x и y = ax при любых значениях параметра a имеют общую точку – начало координат. Пусть x 0. Выразим из уравнения ax = x параметр a через x: a = 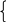 –1, при x 0, 1, при x 0 y  1   y = 1   y = –1 –1 y = a (a 1) y = a (–1 a 0)      0 x y = a (a –1)  При a 1 графики не имеют общих точек, следовательно, корней уравнения кроме x = 0, нет. При a = 1 график функции y = a (y = 1) содержит правую часть графика функции y = При a = –1 график функции y = a (y = –1) содержит левую часть графика функции y = Ответ: при a 1 x = 0; при a = 1 x 0; при a = –1 x 0. Это упражнение является очень полезным, т.к. во многих случаях графический метод более уместен, чем аналитический, а на первых порах следует рассматривать все способы, чтобы выработать у учащихся зоркость в выборе метода решения более сложных задач. Итак, все рассмотренные выше упражнения (123) и им подобные имеют ясную дидактическую цель – помочь учащимся составить представление о параметре, о том, что значит решить уравнение с параметром. Учащиеся 7 класса должны усвоить главное: параметр, будучи фиксированным, но неизвестным числом, имеет как бы двойственную природу. Во-первых, предполагаемая известность позволяет "общаться" с параметром как с числом, а во-вторых, степень свободы общения ограничивается его неизвестностью. Так, деление на выражение, содержащее параметр, требует дополнительного исследования. Как правило, результаты этих исследований влияют и на решение, и на ответ. При решении задач с параметром учитель должен обратить внимание учащихся на необходимость осторожного, деликатного обращения с фиксированным, но неизвестным числом. К концу года учащиеся должны уметь решать задачи типа 16, 9, 10, 18, 19. Регулярно в проверочные и контрольные работы последними заданиями включаются задачи с параметрами. В мае проводится контрольная работа, в которую включены все типы основных задач, однако уровень сложности зависит непосредственно от контингента учащихся. 8 класс. Сейчас перед каждым учеником ставится задача научиться овладевать фундаментальными знаниями, т.е. не набором некоторых правил и умений решать стандартные задачи, а, прежде всего, глубокому пониманию сути изучаемых явлений, приобщению к поиску самих задач, постановке этих задач, формулированию гипотез, испытанию их на правдоподобие. В процессе исследования ребята разрабатывают способы решения поставленной задачи, реализуют их, учатся обобщать полученные результаты, применять их для постановки новых проблем. Уравнения с параметрами, приводимые к линейным. Следующий шаг в изучении уравнений с параметром, составляют уравнения, при решении которых требуется дополнительная проверка, связанная с ограничениями их области определения. При изучении темы "Рациональные дроби" дается определение области допустимых значений переменных, а также условие равенства дроби нулю, что составляет базу для решения таких уравнений. Прежде, чем заняться решением уравнений, мы опять возвращаемся к основам темы "Решение задач с параметрами", но уже на более серьезном теоретическом уровне. Рассмотрим уравнения: Каждое из этих уравнений можно рассматривать как уравнение с переменными x и a. Однако мы говорим о решении уравнения относительно x, считая x и a неравноценными, и хотим выразить x через a, считая a известным. При таком рассмотрении переменная x называется неизвестным, переменная a – параметром. Если параметру, содержащемуся в уравнении, придать некоторое значение, то возможен один из двух случаев: получится уравнение, содержащее лишь данные числа и неизвестные и не содержащее параметров; получится условие, лишенное смысла. В первом случае значение параметра называется допустимым, во втором – недопустимым. (обсудить предъявленные уравнения) Решить уравнение, содержащее параметр – значит, для каждого допустимого значения параметра найти множество всех корней данного уравнения. Условились параметры обозначать первыми буквами латинского алфавита: a, b, c, …, k, l, m, а неизвестные – последними: x, y, z. Перейдем к рассмотрению ключевых уравнений. (подобрать подготовительный материал для устной работы очень легко) Решение: ОДЗ: x 2. Умножим обе части уравнения на x 2 0, получим: a = x 2, x = a + 2. Найдем недопустимые значения a, т.е. решим уравнение: a + 2 = 2, a = 0. (Комментируем: при a = 0 x = 2, но число 2 не входит в область допустимых значений исходного уравнения, следовательно, не может быть его корнем). Ответ: при a 0 x = a + 2; при a = 0 корней нет. Решение: ОДЗ: x 1, a 0. Умножим обе части уравнения на a (x + 1) 0, получим: a (x – 4) + 2x + 2 = 1, (a + 2) x = –1 + 4a. (1) Найдем недопустимые значения a: (комментарий: подставим x = –1 в уравнение (1)): (a + 2) (–1) = –1 + 4a, –a – 2 = –1 –5a = 1, a = – При a = – (Комментарий: решим уравнение (1), это линейное уравнение относительно x, решение которого изучено в 7 классе.) (a + 2) x = –1 + 4a 1. Если a + 2 0, a –2, то x = 2. Если a + 2 = 0, a = –2, то 0 x = – 9, корней нет. (Комментарий: обратите серьезное внимание на выписку ответа, можно упустить некоторые моменты). Ответ: при a –2, a – при a = –2, a = – Вторую часть ответа можно выписать и следующим образом: при a = –2, a = – при a = 0 левая и правая части уравнений не имеют смысла. Решение: ОДЗ: kx 12 0;x 3x – k 0; x Умножим обе части уравнения на (kx – 12) (3x – k) 0, получим: 3 (3x – k) = kx – 12, 9x – 3k = kx – 12, 9x – kx = 3k – 12, (9 – k) x = 3k – 12. (1) Найдем недопустимые значения k: 1. Если x = 108 – 12k= 3k2 – 12, k2 = 36, k = 6. 2. Если x = 9k – k2 = 9k – 36, k2 = 36, k = 6. При k = 6 корней нет. Решим уравнение (9 – k) x = 3k – 12. 1. Если 9 – k 0, k 9, то x = 2. Если 9 – k = 0, k = 9, то 0 x = 15, корней нет. Ответ: при k 6, k 6, k 15 x = при k = 6, k = 6, k = 15 корней нет. Каждое из этих трех уравнений должно быть основательно проработано в классе, так как в их решении есть "подводные камни", которые должны преодолеть восьмиклассники. Далее можно предложить учащимся самостоятельно составить словесное описание алгоритма решения таких уравнений. Алгоритм решения уравнения с параметрами, сводящегося к линейному. Найти область допустимых значений неизвестного и параметров, входящих в уравнение. Умножить обе части уравнения на общий знаменатель, преобразовать к виду линейного. Найти недопустимые значения параметра. Решить линейное уравнение с параметром. Выписать ответ с учетом пунктов 3, 4. Для формирования навыка решим следующие уравнения: Решение: ОДЗ: x –1; Умножим обе части уравнения на x + 1 0, получим: x = a (x + 1), x = ax + a, x – ax = a, (1 – a) x = a. Найдем недопустимые значения a: Если x = –1, то (1 – a) (– 1) = a, a – 1 = a, 0 a = 1, корней нет. Не существует значений a, при которых x = –1. (1 – a) x = a. 1. Если 1 – a 0, a1, то x = 2. Если 1 – a = 0, a = 1, то 0 x = 1, корней нет. Ответ: при a 1 x = при a = 1 корней нет. Ответ: при a 1 x = a; при a = 1корней нет. Решение: ОДЗ: x –3; x 2; a –1; Упростим уравнение: После преобразований, которые учащиеся выполняют самостоятельно, получим: 2ax = 1 – a. Найдем недопустимые значения a: 1. Если x = –3, то 2a (–3) = 1 – a, –6a = 1 – a, –5a = 1, a = –0,2. 2. Если x = 2, то 2a 2 = 1 – a, 5a = 1, a = 0,2. При a = 0,2 корней нет. 2ax = 1 – a. 1. Если 2a 0, a0, то x = 2. Если 2a = 0, a = 0, то 0 x = 1, корней нет. Ответ: при a –1, a 0,2, a 0 x = при a = –1, a = 0,2, a = 0корней нет. Ответ: при m 1, m –0,4 , m 2,25 x = при m = –0,4 , m = 2,25 , корней нет; при m = 1 уравнение не имеет смысла. Следующие два уравнения можно отнести в банк задач и рассмотреть их решение в любое удобное время вплоть до 11 класса. Решение: ОДЗ: x –3a; x –b. a (b + x) = 6a + 2x, (a – 2) x = a (6 – b). Найдем недопустимые значения aи b: 1. Если x = –3a, то (a – 2) (–3a) = a (6 – b); a (b – 3a) = 0;  a = 0, a = 0,b = 3a. 2. Если x = –b, то (a – 2) (–b) = a (6 – b), 2b = 6a, b = 3a. При a = 0 и b = 3aкорней нет. (a – 2) x = a (6 – b). 1. Если a – 2 0, a2, то x = 2. Если a – 2 = 0, a = 2, то 0 x = 2 (6 – b), а) при b 6 0 x = 12 – 2b, корней нет; б) при b = 6 0 x = 0, x – любое число. Ответ: при a 0, a 2, b 3a x = при a = 0 корней нет; при a = 2, b 6 корней нет; при a = 2, b = 6 x – любое число; при a 2, b = 3aкорней нет. Задачу можно усложнить, потребовав исследовать знаки корней, тогда в ответе появится дополнение: x 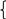 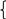 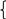 0 при a 0, 0 a 2, a 2, 0 при a 0, 0 a 2, a 2,b 6; b 6; b 6; x = 0 при b = 6; x    0 при a 0, 0 a 2, a 2, 0 при a 0, 0 a 2, a 2,b 6; b 6; b 6. Аналогичным требованием можно усложнить задачу 3, тогда: x 0 при k (4; 6) U(6; 9), x = 0 при k = 4; x 0 при k (; 6) U( 6; 4) U(9; ). Требуется применить метод интервалов. Решение: ОДЗ: a R, b R, x b2. Умножим обе части уравнения на b4 – x2 0 (a – b)2x = a2 – b2. Найдем недопустимые значения aи b (ab): 1. Если x = b2, то (a – b)2b2 = a2 – b2; a = 2. Если x = –b2, то (a – b)2( b2) = a2 – b2, a = При a = (a – b)2x = a2 – b2. 1. Если (a – b)2 0, a b, то x = x = 2. Если (a – b)2 = 0, a = b, то 0 x = 0, x – любое число, кромеx = b2(из ОДЗ). Ответ: при a b, a при a = b, x – любое число, кроме b2; при a = При решении уравнений такого вида от учащихся требуется строгое соблюдение алгоритма. Если позволять менять местами шаги 3 и 4, то практика показывает, что шаг 3 учащиеся в решении теряют. Также обращается особое внимание на строгость порядка при выписке ответа, рассмотрение последовательно всех значений параметра согласно решению. Из ранее изученного восьмиклассникам на факультативе можно предложить такие задания: Решить уравнение x2 – 1 + a (x – 1) = 0. Решение: Это уравнение равносильно системе  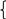 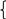  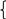  x2 – 1 = 0, x2 – 1= 0, x = –1, x = –1, x2 – 1 = 0, x2 – 1= 0, x = –1, x = –1,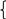 a (x – 1) = 0; a (x – 1) = 0; a (x – 1) = 0; a = 0; a (x – 1) = 0; a (x – 1) = 0; a (x – 1) = 0; a = 0; x = 1, x = 1, x = 1, x = 1,  a (x – 1) = 0; a – любое число. a (x – 1) = 0; a – любое число.Ответ: при a 0, x = 1; при a = 0, x = 1. Найти все значения параметра bтакие, что при любых значениях параметра a система:  x – 2y = a,(1) x – 2y = a,(1)ax + 3y = b(2) имела хотя бы одно решение. Решение: Систему решаем методом подстановки.  y = y =ax + 3y = b. Подставим yв уравнение (2), получим: ax + (a + Если a + 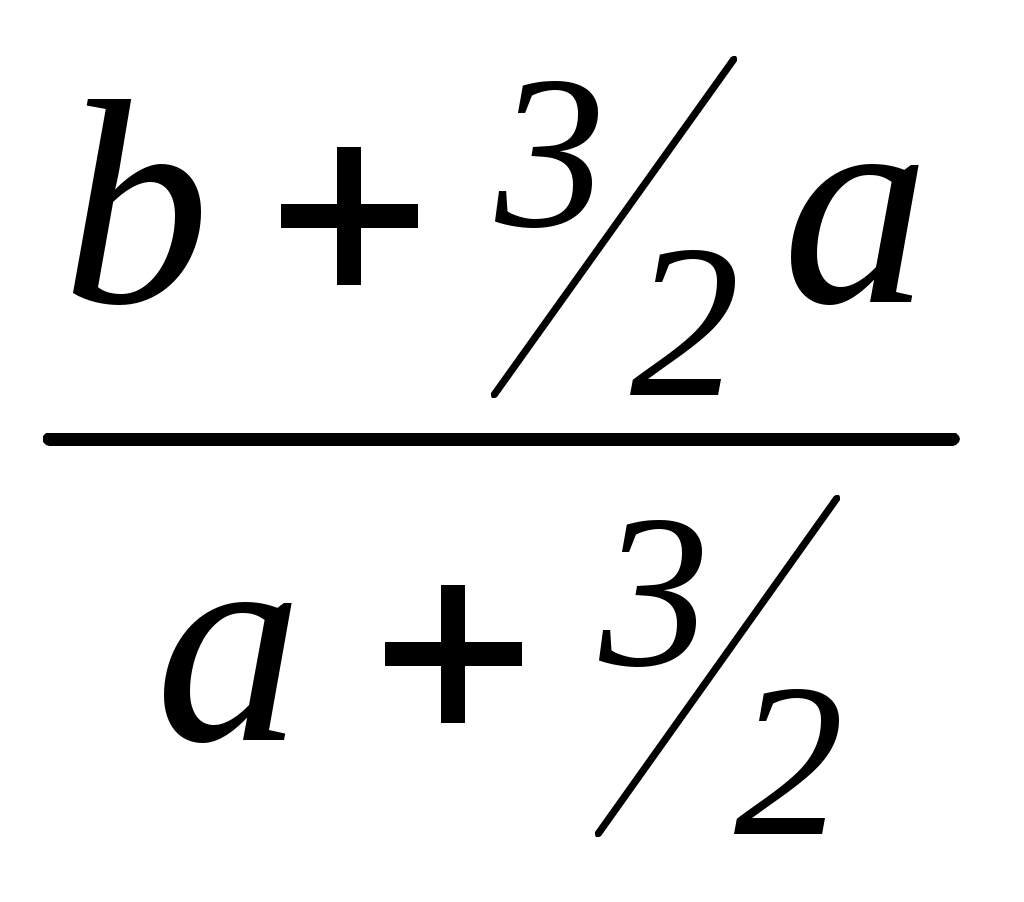 . .Уравнение, а значит, и система, имеют решение при любом действительном b. Если a + Уравнение имеет решение при b = Значит, независимо от значения aсистема будет иметь решения при b = Ответ:b = В восьмом классе более серьезно изучаются графики функции. Восьмиклассники знакомы с элементарными преобразованиями графиков. Поэтому я считаю целесообразным после изучения функции y = Сколько корней имеет уравнение x 2 = a при различных значениях параметра a? Решение: Построим график функции y = x 2, проведя ряд последовательных преобразо-ваний: y = x – 2 y = x 2 y = x 2 , и график функции y = a. y  y = x 2 y = a (a 2) 2    y = a (a = 2)       y = a (0 a 2)        x y = a (a = 0) 2 0 2     y = a (a 0)  Ответ: при a 0 корней нет; при a = 0 два корня; при 0 a 2 четыре корня; при a = 2 три корня; при a 0 два корня. Решить уравнение x 1 + x 3 = a. Решение: Построим графики функций y = x 1 + x 3и y = a. 4 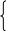 – 2xпри x 1, – 2xпри x 1, y = x 1 + x 3 = 2 при 1 x 3, 2x – 4 при x 3. y = x 1 + x 3 y   y = a (a 2) 2     y = a (a = 2)      y = a (a 2)  x 1 0    3  Если a 2, то ломаная и прямая y = aне пересекаются. Уравнение корней не имеет. Если a = 2, то ломаная и прямая совпадают при 1 x 3. Уравнение имеет бесконечно много корней. Если a 0, то ломаная и прямая пересекаются в двух точках. Уравнение имеет два корня: 4 – 2x = aили 2 – 4x = a; x = Ответ: при a 2 корней нет; при a = 2, 1 x 3; при a 2, x1 = Рассмотрим более сложный, но доступный восьмикласснику пример. Сколько решений в зависимости от a имеет уравнение x + 2 = ax + 1? Решение: При x = 0 получаем 0 + 2 = a 0 + 1, т.е. x = 0 не является корнем уравнения ни при каких значениях параметра a. Преобразуем уравнения с учетом, что x 0. Построим графики функций y = y  = = 1 – График функции y = График функции y = – При различных значениях параметра aграфиками функций y = a являются прямые, параллельные оси абсцисс. 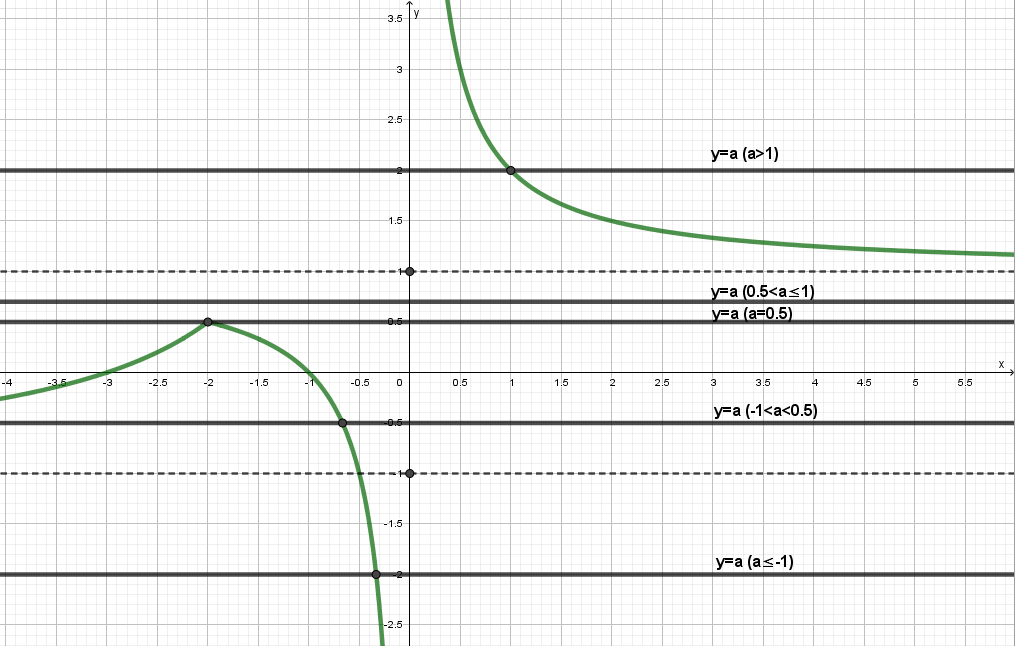 При a1 иa 1 графики имеют одну общую точку пересечения, уравнение имеет один корень; При 1a ½ точек пересечения две, уравнение имеет два корня; При ½ a 1 точек пересечения нет, уравнение корней не имеет; При a = ½ один корень. Ответ: при a1 один корень; при 1a ½ два корня; при a = ½ один корень; при ½ a 1 корней нет; при a 1 один корень.  Пока мы не формулируем четкий алгоритм применения графического метода, только лишь устно составляем план решения задачи. Рассмотрение же таких задач с восьмиклассниками считаю необходимым, иначе в 10-11 классах при подготовке к экзаменам придется начинать все сначала, значит, теряется драгоценное время, ведь восстанавливать материал гораздо легче, чем изучать заново. Пока мы не формулируем четкий алгоритм применения графического метода, только лишь устно составляем план решения задачи. Рассмотрение же таких задач с восьмиклассниками считаю необходимым, иначе в 10-11 классах при подготовке к экзаменам придется начинать все сначала, значит, теряется драгоценное время, ведь восстанавливать материал гораздо легче, чем изучать заново.ЛИНЕЙНЫЕ НЕРАВЕНСТВА С ПАРАМЕТРАМИ Основная цель: сформировать умение решать элементарные линейные неравенства с параметрами. В первую очередь расширим определение линейного неравенства. Каждое из неравенств вида AxB, AxB, AxB, AxB, где Aи B – действительные числа или функции от параметров, а x– неизвестная величина, называется линейным неравенством с одним неизвестным (x). Рассмотрим простейший пример: Решить неравенство ax 1. Невнимательный ученик быстро дает ответ x  ax 1 ax 1   a 0a = 0a 0 ax 1 0x 1 ax 1    x Учитель задает по заданию такие вопросы: "Каким будет решение, если вместо числа 1 записать ? вместо знака записать знак ?" и т.п. Ученики активно анализируют ответы своих одноклассников. Затем учащиеся получают задание по вариантам составить блок-схемы к решению неравенств AxB, AxB, AxB, AxB. В тетрадях записываем словесное описание алгоритма. Алгоритм решения линейных неравенств с параметрами На примере неравенства Ax B,где x – неизвестное, A, B – выражения, зависящие только от параметров) Если A 0, то x Решением неравенства являются все числа из промежутка ( а) Если A = 0, B 0 0 x B, x – любое число. Решением неравенства является промежуток ( + ). б) Если A = 0, B = 0 0 x 0, решений нет. в) Если A = 0, B 0 0 x B, решений нет. Если A 0, то x Решением неравенства является промежуток ( Так как учащиеся еще не знакомы с методом интервалов, то выбор заданий по этой теме весьма ограничен. На этом этапе работы будет достаточно, если школьники усвоят решение простейших ключевых неравенств. Решить неравенство (m – 1)x 5m. Решение: Если m – 1 0, m 1, то x Если m – 1 = 0, m = 1, получим 0 x 5, x – любое число. Если m – 1 0, m 1, то x Ответ: при m 1, x при m = 1, x – любое число; при m 1, x Несущественно, будут ли значения m и x записаны в форме неравенства или промежутка. 2ax + 5 a + 10x, 2ax – 10x a – 5, (2a – 10)x a – 5, 2(a – 5)x a – 5. Если 2(a – 5) 0, a – 5 0, a 5, то x Если 2(a – 5) = 0, a – 5 = 0, a = 5, то 0 x 0, решений нет. Если 2(a – 5) 0, a – 5 0, a 5, то x Ответ: при a 5, x при a = 5, решений нет; при a 5, x mx – 6 2m – 3x, mx + 3x 2m + 6, (m + 3)x 2(m + 3). Если m+3 0, m3, то x Если m+3 = 0, m = 3, то 0 x 0, x – любое число. Если m+3 0, m3, то x Ответ: при m3, x 2; при m = 3, x – любое число; при m3, x 2. Формальное решение неравенств 17, 18 приводит к распространенной ошибке, которая сводится к делению левой и правой частей неравенства на выражение, содержащее переменную, а это приводит к потере решений и коротким ответам. Неправильно: x(m + 3) 2(m + 3), x 2. 5x – a ax – 3. Ответ: при a 5, x при a = 5, решений нет; при a 5, x |
