Задачи с параметрами в курсе основной школы. #Задачи с параметрами в курсе основной школы. Александры Анатольевны

• Название: Александры Анатольевны
• Анкор: Задачи с параметрами в курсе основной школы
• Дата: 06.05.2023
• Размер: 1.31 Mb.
• Имя файла: #Задачи с параметрами в курсе основной школы.doc
• Тип: Документы; #1112281
• страница: 4 из 8

Задачи на повторение

12. 
    При каких значениях a уравнение 1 + 3x – ax = 2 + x имеет отрицательный корень?
    

Ответ: при a  2.

12. 
    При каких значениях a уравнение a(3x – a) = 6x – 4 имеет одно положительное решение?
    

Ответ: при a 2, a  2.

12. 
    При каких значениях a уравнение a(x – 1) = x – 2 имеет решение, удовлетворяющее условию x 1?
    

Ответ: при a  1.

Когда изучены системы линейных уравнений, можно решить такие задачи.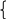

12. 
    П ри каких значениях a система уравнений x + y = a, имеет решение x0, y0?
    

2x + y = 3

Ответ: при a  3.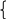

12. 
    П ри каких значениях a система уравнений x + 3y = 2a – 1, имеет решение x0, y0?
    

x – y = a

Ответ: при 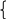 a  1.

12. 
    П ри каких значениях a система уравнений 3x – y = 1 – a, имеет решение x 1, y 4?
    

x + y = 2a + 1

Ответ: при a = 2.

Системы 23, 24, 25 решаются подстановкой.

Если учащиеся 8 класса научены решать неравенства с модулем, то полезны такие упражнения.

12. 
    Для каждого значения a решите неравенство:
    

а) x – 3aб) x – 2a

Ответ: при a  0, 3 – ax 3 + a;Ответ: при a  0, решений нет;

при a  0 решений нет. при a = 0, x = 2;

при a  0, 2 – a  x  2 + a.

в) x + 5 a г) 3 – 2x a

Ответ: при a  0, x – любое число; Ответ: при a  0, x – любое число;

при a = 0, x –5; при a0, x или x .

при a  0, x  – a – 5 или x  a – 5.

12. 
    При каких значениях a неравенство справедливо при любом значении x:
    

а) x a б) x + 2a – 1  0 в) a x – 1  0 г) 2 3 – 5x + 2 – 3a  0

Ответ: a  0. Ответ: a  . Ответ: a  0. Ответ: a  .

Интересны для учащихся, увлекающихся математикой, нестандартные задачи, решение которых требует хорошего знания теории.

12. 
    При каких a уравнение ax = a²равносильно неравенству x – 3 a ?
    

Решение: Решим уравнение ax = a².

4. 
   Если a  0, то x = = a,
   

уравнение имеет один корень: x = a.

5. 
   Если a = 0, то 0 x = 0, x – любое число,
   

уравнение имеет бесконечное множество решений.

Решим неравенство x – 3 a.

1. 
   Если a  0, то x – любое число.
   
2. 
   Если a  0, то x  3 – a или x  a + 3.
   

Решением неравенства является объединение двух промежутков.

Следовательно, требованию задачи удовлетворяет только a = 0.

Ответ: a = 0.

12. 
    При каких a неравенство 2x + a  0 является следствием неравенства x + 1 – 3a  0 ?
    

Решение: Решим неравенство 2x + a  0;x  – , x + 1 – 3a  0, x  3a – 1.

По условию, множество решений неравенства x  – должно содержать множество решений неравенства x  3a – 1. Это требование выполняется, если –  3a – 1, т.е. a  .

Ответ: a  .

12. 
    При каких a неравенство x  a является следствием неравенства x a ?
    

Решение: Решим неравенство x a.

1. 
   Если a  0, то решений нет.
   
2. 
   Если a  0, то –a  x  a.
   

Очевидно, что при a  0 рассматриваемые неравенства не имеют ни одного общего решения.

При a  0 неравенство x a не имеет решений, а неравенство x  a, играющее роль неравенства–следствия, имеет решения. Это нас устраивает.

Ответ: a  0.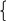

12. 
    П ри каких значениях параметра a система неравенств ax + 1  0,
    

x + a  0

имеет хотя бы одно решение?

Решение:

1.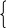 
   П ри a  0 данная система равносильна системе x  – ,
   

x  –a.

Решением системы является интервал (x₁; +),где x₁–наибольшее их чисел – и 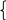–a.

2. 
   П ри a = 0 0 x + 1  0,
   

x + 0  0.

Решением системы является интервал (0; +).

3.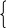 
   П ри a  0 система равносильна системе x  – ,
   

x  –a.

Эта система имеет решение, если –a  – . Решим это неравенство с учетом условия a  0. Получим a² 1, a 1, –1  a  0 (см. условие).

4. 
   Объединим найденные значения a в каждом из рассмотренных случаев.
   

Ответ: a  –1.

В заключение приведу еще пример решения линейного неравенства при некоторых начальных условиях.

12. 
    При каких значениях k неравенство (k – 1)x + 2k + 1  0 верно при всех значениях x, удовлетворяющих условию x 3 ?
    

Решение:

Рассмотрим функцию y = (k – 1)x + 2k + 1. Она является линейной при любом действительном значении k, т.е. графиком ее служит прямая.


y

y

y


k 

k = 

k 

3

0

0

0

x

x

x

3

3

3

3

3


Д 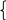ля выполнения неравенства на всем отрезке 3; 3 достаточно выполнения условия y (3)  0,

y (3)  0.

y (3) = 3(k – 1) + 2k + 1 = 4  k,

y (3) = 3(k – 1) + 2k + 1 = 5k  2.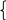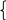

4 – k  0, k  4, 0,4  k  4.

5k – 2  0; k  0,4;

Ответ: 0,4  k  4.

К обязательным результатам по этой теме относится умение решать задачи типа 16, 17, 18, 23, 24, поэтому контролирующие работы составляются с учетом этого требования.