Для оценки устойчивости по критерию Михайлова необходимо построить кривую, которую описывает конец вектора D(jw) на комплексной плоскости при изменении частоты w от 0 до бесконечности, называемую годографом Михайлова. Вектор D(jw) получаем из характеристического полинома замкнутой системы (8)
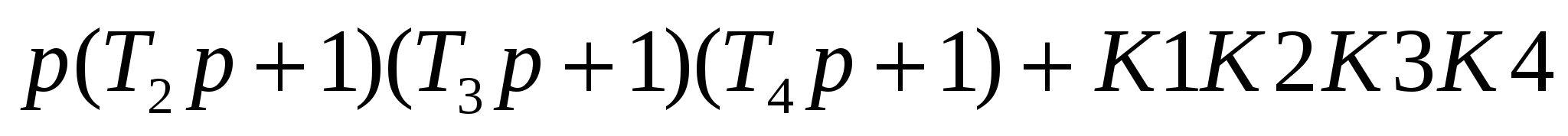

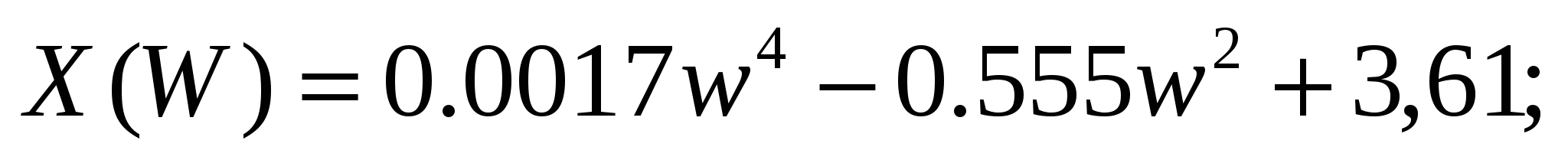 (10) (10)
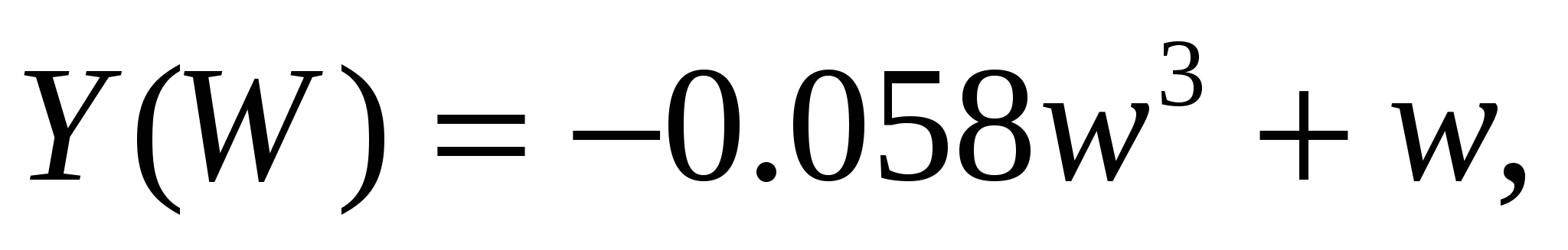 (11) (11)
Используя ЭВМ, построим годограф Михайлова и проанализируем его.
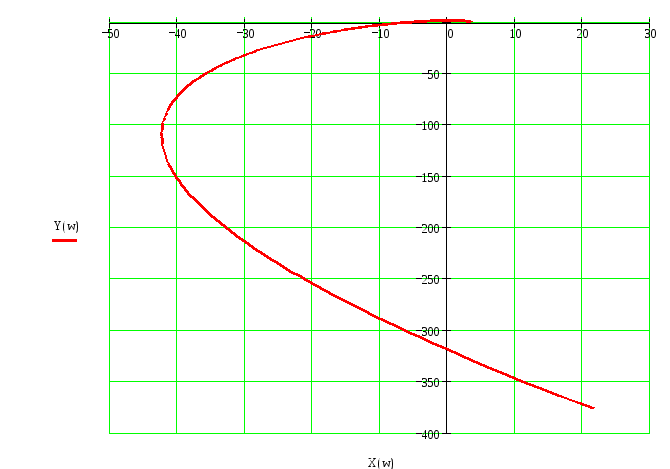
Рисунок 3 - Годограф Михайлова
Для устойчивости системы необходимо, чтобы годограф Михайлова обошёл в положительном направлении (против часовой стрелки) последовательно n-квадрантов, нигде не обращаясь в нуль. В нашем случае годограф из первой четверти попадает во вторую, затем в третью и четвёртую, то есть он обходит четыре квадранта, а значит, система устойчивая.
Получим частотную передаточную функцию разомкнутой системы W(jw), для чего в выражение для передаточной функции разомкнутой системы подставляем p=jw
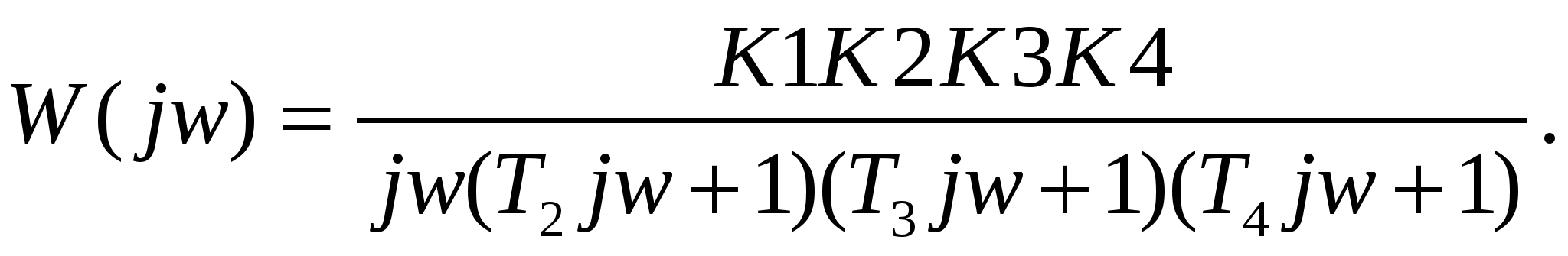 (12) (12)
Преобразуя выражение (12) получим
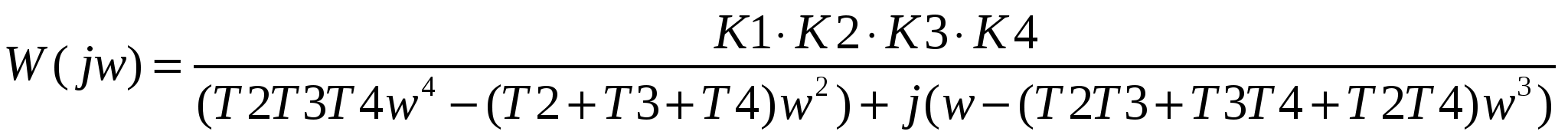
 , (13) , (13)
где U1 и V1 – действительная и мнимая части частотной передаточной функции W(jw), равные
 (14) (9) (14) (9)
 (15) (10) (15) (10)
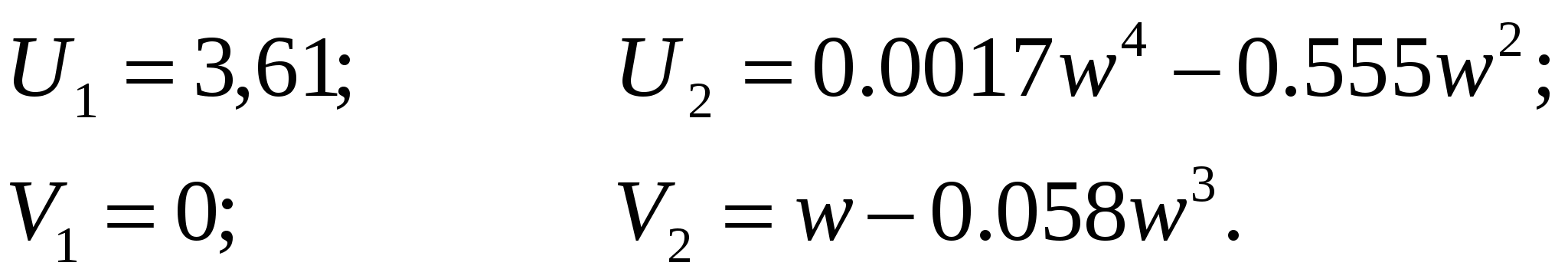
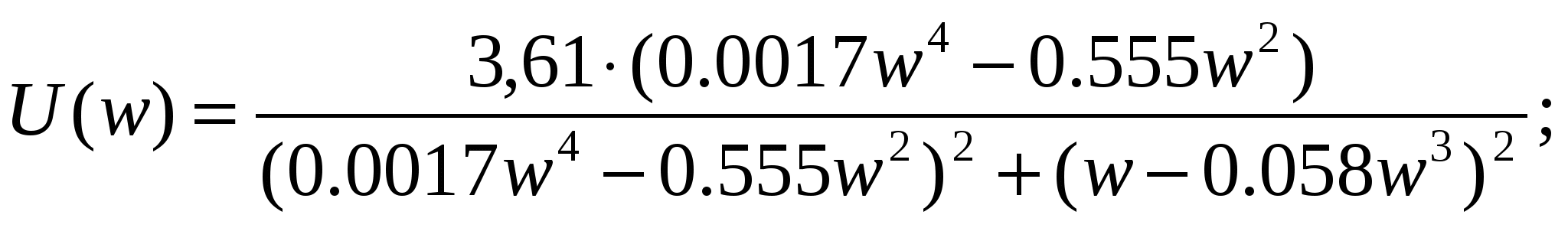 (16) (16)
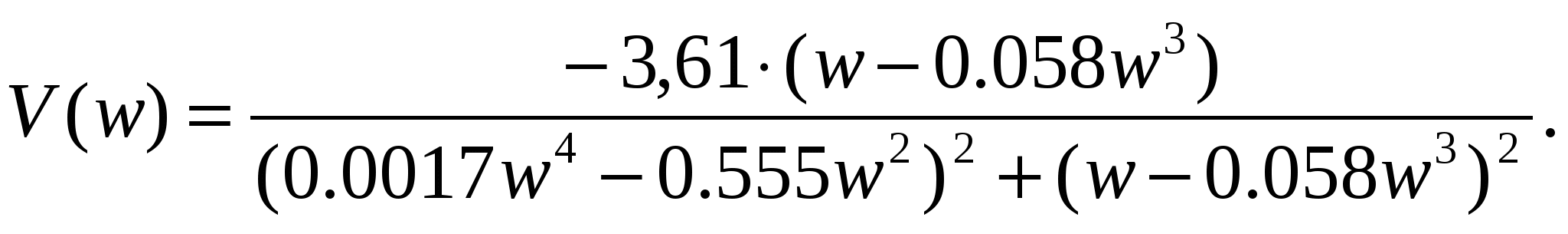 (17) (17)
Таблица 1 – Координаты АФЧХ
w
|
u1(w)
|
u2(w)
|
v1(w)
|
v2(w)
|
U(w)
|
V(w)
|
|
0,1
|
3,61
|
-0,0055498
|
0
|
0,099942
|
-1,9996485
|
-36,009909
|
|
0,3
|
3,61
|
-0,0499362
|
0
|
0,298434
|
-1,9689463
|
-11,767018
|
|
0,6
|
3,61
|
-0,1995797
|
0
|
0,587472
|
-1,8716003
|
-5,5091419
|
|
0,9
|
3,61
|
-0,4484346
|
0
|
0,857718
|
-1,7281109
|
-3,3053465
|
|
1,2
|
3,61
|
-0,7956749
|
0
|
1,099776
|
-1,5588719
|
-2,1546613
|
|
Окончание таблицы 1
|
1,5
|
3,61
|
-1,2401438
|
0
|
1,30425
|
-1,3821812
|
-1,4536298
|
|
1,8
|
3,61
|
-1,7803541
|
0
|
1,461744
|
-1,2112037
|
-0,9944481
|
|
2,1
|
3,61
|
-2,4144882
|
0
|
1,562862
|
-1,0536745
|
-0,6820277
|
|
2,4
|
3,61
|
-3,1403981
|
0
|
1,598208
|
-0,9130558
|
-0,4646713
|
|
2,7
|
3,61
|
-3,955605
|
0
|
1,558386
|
-0,7900103
|
-0,3112396
|
|
3
|
3,61
|
-4,8573
|
0
|
1,434
|
-0,6836275
|
-0,2018244
|
|
3,3
|
3,61
|
-5,8423434
|
0
|
1,215654
|
-0,5922604
|
-0,1232354
|
|
3,6
|
3,61
|
-6,9072653
|
0
|
0,893952
|
-0,5140281
|
-0,0665265
|
|
3,9
|
3,61
|
-8,048265
|
0
|
0,459498
|
-0,4470866
|
-0,0255254
|
|
4,2
|
3,61
|
-9,2612117
|
0
|
-0,097104
|
-0,389755
|
0,00408659
|
|
4,5
|
3,61
|
-10,541644
|
0
|
-0,78525
|
-0,3405616
|
0,02536853
|
|
4,8
|
3,61
|
-11,884769
|
0
|
-1,614336
|
-0,2982473
|
0,04051163
|
|
5,1
|
3,61
|
-13,285466
|
0
|
-2,593758
|
-0,2617487
|
0,05110193
|
|
5,4
|
3,61
|
-14,73828
|
0
|
-3,732912
|
-0,2301745
|
0,0582986
|
|
5,7
|
3,61
|
-16,23743
|
0
|
-5,041194
|
-0,2027799
|
0,06295655
|
|
6
|
3,61
|
-17,7768
|
0
|
-6,528
|
-0,1789431
|
0,06571151
|
|
6,3
|
3,61
|
-19,349947
|
0
|
-8,202726
|
-0,1581447
|
0,06703984
|
|
6,6
|
3,61
|
-20,950095
|
0
|
-10,074768
|
-0,1399497
|
0,06730091
|
|
6,9
|
3,61
|
-22,570139
|
0
|
-12,153522
|
-0,123993
|
0,0667675
|
|
7,2
|
3,61
|
-24,202644
|
0
|
-14,448384
|
-0,1099672
|
0,06564771
|
|
7,5
|
3,61
|
-25,839844
|
0
|
-16,96875
|
-0,0976123
|
0,06410096
|
|
7,8
|
3,61
|
-27,47364
|
0
|
-19,724016
|
-0,086708
|
0,06224982
|
|
8,1
|
3,61
|
-29,095607
|
0
|
-22,723578
|
-0,0770665
|
0,06018871
|
|
8,4
|
3,61
|
-30,696987
|
0
|
-25,976832
|
-0,0685277
|
0,05799043
|
|
8,7
|
3,61
|
-32,268691
|
0
|
-29,493174
|
-0,0609539
|
0,0557111
|
|
9
|
3,61
|
-33,8013
|
0
|
-33,282
|
-0,054227
|
0,05339391
|
|
9,3
|
3,61
|
-35,285066
|
0
|
-37,352706
|
-0,0482449
|
0,05107196
|
|
9,6
|
3,61
|
-36,709908
|
0
|
-41,714688
|
-0,0429191
|
0,04877042
|
|
9,9
|
3,61
|
-38,065418
|
0
|
-46,377342
|
-0,0381729
|
0,04650831
|
|
10,2
|
3,61
|
-39,340853
|
0
|
-51,350064
|
-0,0339394
|
0,04429975
|
|
11
|
3,61
|
-42,2653
|
0
|
-66,198
|
-0,0247349
|
0,03874096
|
|
11,8
|
3,61
|
-44,318978
|
0
|
-83,495856
|
-0,0179047
|
0,033732
|
|
12,6
|
3,61
|
-45,263746
|
0
|
-103,42181
|
-0,012821
|
0,02929434
|
|
13,4
|
3,61
|
-44,844751
|
0
|
-126,15403
|
-0,009031
|
0,02540549
|
|
14,2
|
3,61
|
-42,790428
|
0
|
-151,8707
|
-0,0062048
|
0,02202198
|
|
15
|
3,61
|
-38,8125
|
0
|
-180,75
|
-0,0040996
|
0,01909202
|
|
15,8
|
3,61
|
-32,60598
|
0
|
-212,9701
|
-0,0025357
|
0,01656251
|
|
16,6
|
3,61
|
-23,849167
|
0
|
-248,70917
|
-0,0013792
|
0,01438269
|
|
17,4
|
3,61
|
-12,20365
|
0
|
-288,14539
|
-0,0005297
|
0,01250597
|
|
18,2
|
3,61
|
2,68569392
|
0
|
-331,45694
|
8,8243E-05
|
0,01089059
|
|
19
|
3,61
|
21,1907
|
0
|
-378,822
|
0,0005314
|
0,00949982
|
|
20,6
|
3,61
|
70,6185963
|
0
|
-486,42533
|
0,0010552
|
0,0072683
|
|
21,4
|
3,61
|
102,368715
|
0
|
-547,01995
|
0,00119322
|
0,0063761
|
|
23
|
3,61
|
182,1347
|
0
|
-682,686
|
0,00131703
|
0,00493656
|
|
24,6
|
3,61
|
286,707864
|
0
|
-838,84229
|
0,00131705
|
0,0038534
|
|
25,4
|
3,61
|
349,529624
|
0
|
-925,04971
|
0,00129033
|
0,00341494
|
|
26,2
|
3,61
|
420,065585
|
0
|
-1016,9142
|
0,00125266
|
0,00303251
|
|
27
|
3,61
|
498,8547
|
0
|
-1114,614
|
0,00120765
|
0,0026983
|
|
27,8
|
3,61
|
586,452632
|
0
|
-1218,3272
|
0,00115799
|
0,00240567
|
|
29,4
|
3,61
|
790,381156
|
0
|
-1444,5067
|
0,00105236
|
0,00192331
|
|
30,2
|
3,61
|
907,906635
|
0
|
-1567,3293
|
0,000999
|
0,00172459
|
|
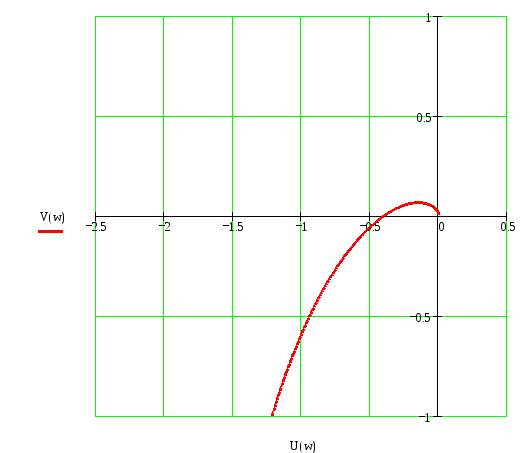
Рисунок 4 – График АФЧХ разомкнутой системы
Согласно условию устойчивости по критерию Найквиста для устойчивости замкнутой системы необходимо и достаточно, чтобы АФЧХ разомкнутой системы не охватывала точку с координатами (-1,j0).
Для данной системы это условие выполняется, АФЧХ разомкнутой системы не охватывает точку с координатами (-1,j0), следовательно, система устойчива.
АФЧХ данной системы пересекает вещественную ось в точке с координатами (-0.4;0) на частоте w=4.17 Гц.
|
 Скачать 1.41 Mb.
Скачать 1.41 Mb.

