Курсовая работа - Анализ и синтез САР. Анализ и синтез линейной системы автоматического регулирования

• Название: Анализ и синтез линейной системы автоматического регулирования
• Дата: 26.04.2018
• Размер: 1.41 Mb.
• Имя файла: Курсовая работа - Анализ и синтез САР.doc
• Тип: Пояснительная записка; #42246
• страница: 2 из 10

Введение

Темой работы является анализ и синтез замкнутой линейной системы автоматического регулирования САР. Выполнение курсовой работы способствует более глубокому пониманию курса и получению практических навыков расчета и проектирования систем автоматического регулирования.

При выполнении курсового проекта решаются вопросы, охватывающие почти все разделы теории стационарных непрерывных линейных систем автоматического регулирования.

Большое внимание уделено преобразованию структурных схем и составлению передаточных функций системы, различным способам исследования устойчивости, построению переходного процесса, оценке качества систем в установившемся и переходном режимах, а также синтезу корректирующего устройства, обеспечивающего заданные показатели качества регулирования.

Решение отдельных задач курсового проекта требует применения справочного материала (номограмм, диаграмм, таблиц и пр.), основная часть которого приводится в методических указаниях.

Приведенные методы расчета позволяют решать задачи с использованием электронной вычислительной техники на основе стандартных программ современных ЭВМ.

1 Анализ линейной системы автоматического регулирования

1.1 Преобразование структурной схемы и определение передаточных функций системы

Приведем заданную структурную схему к одноконтурной с помощью последовательных преобразований (рисунок 2).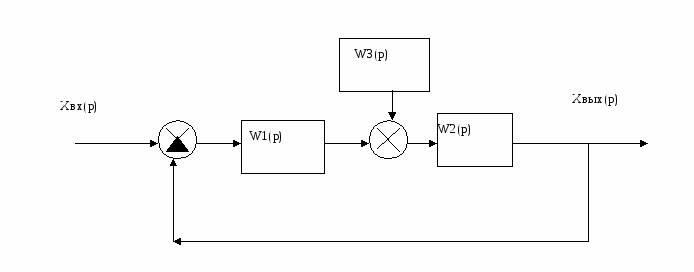

Рисунок 2 – Преобразование исходной структурной схемы

На рисунке 2 приняты следующие обозначения:

  передаточные функции элементов прямой цепи;

  передаточная функция возмущающего воздействия;

  входной и выходной сигналы соответственно.

Передаточные функции элементов прямой цепи:
, , (1)
Передаточная функция возмущающего воздействия
. (2)
Передаточная функция разомкнутой системы
, (3)
где   общий коэффициент усиления прямой цепи;

Подставив численные значения, получим
. (4)
Передаточная функция замкнутой системы по задающему воздействию
, (5)
где   общий коэффициент усиления замкнутой системы;

Подставив численные значения, получим
. (6)
Характеристическое уравнение замкнутой АСР получается путем выделения знаменателя передаточной функции (6) и приравнивания его к нулю
a₀pⁿ + a₁p^n-1 + a₂p^n-2 +…+ a_n=0;

(7)

1.2 Исследование системы на устойчивость по критерию Гурвица

Характеристическое уравнение замкнутой САР получается путем выделения знаменателя передаточной функции (6) и приравнивания его к нулю


. (8)

(5)

Подставим численные значения параметров К и Т в (8) и получим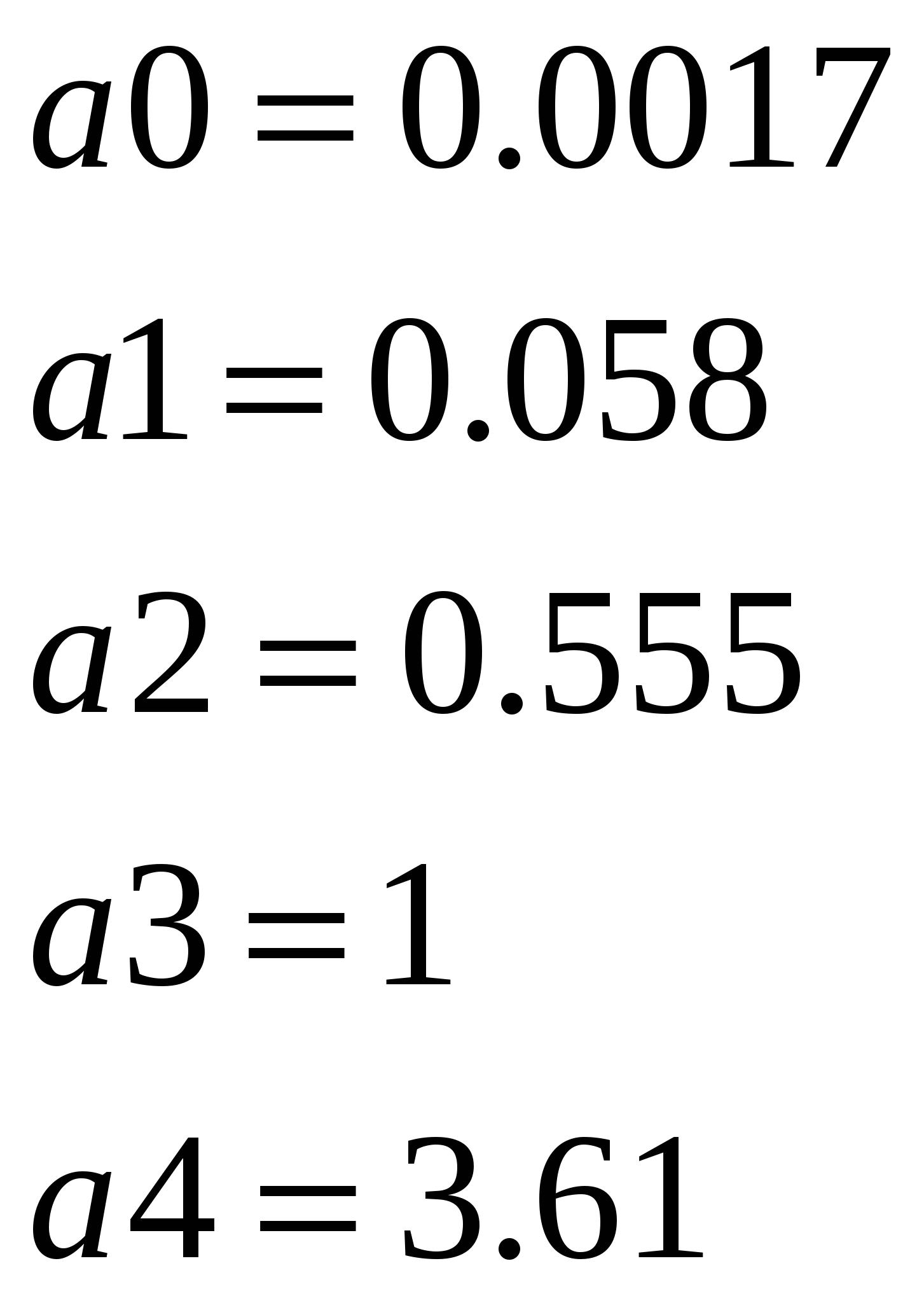








Составим матрицу Гурвица из коэффициентов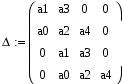
. (9)

Получаем матрицу 4*4

.

Найдём определители Гурвица, выделяя в главном определителе диагональные миноры, очеркивая строки и столбцы: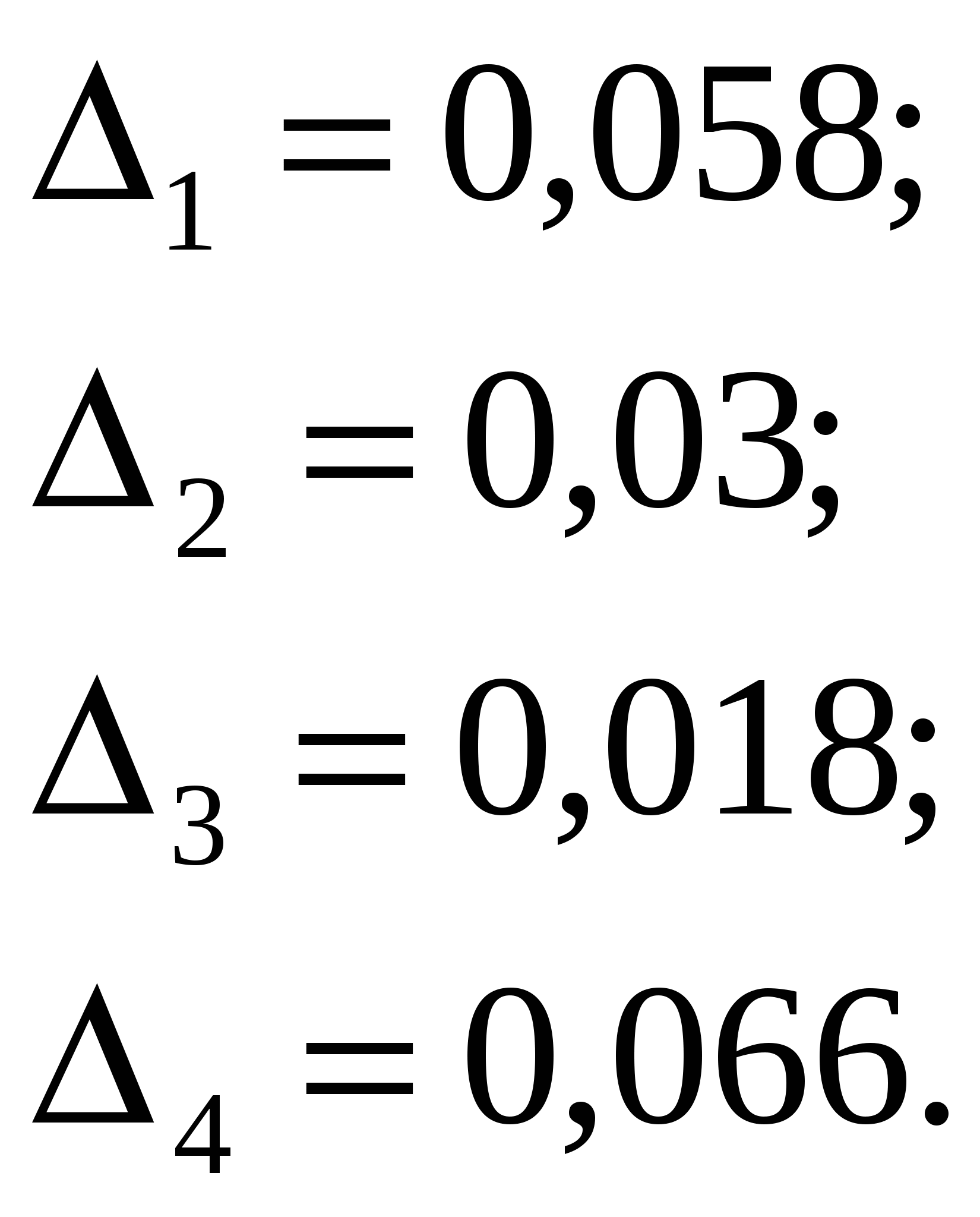



Условия устойчивости для системы четвертого порядка:



Данные условия выполняются.

Все определители матрицы Гурвица больше нуля, коэффициенты больше нуля, следовательно, система устойчивая.

Критический коэффициент находят из уравнения Δ_n-1=0. Обозначим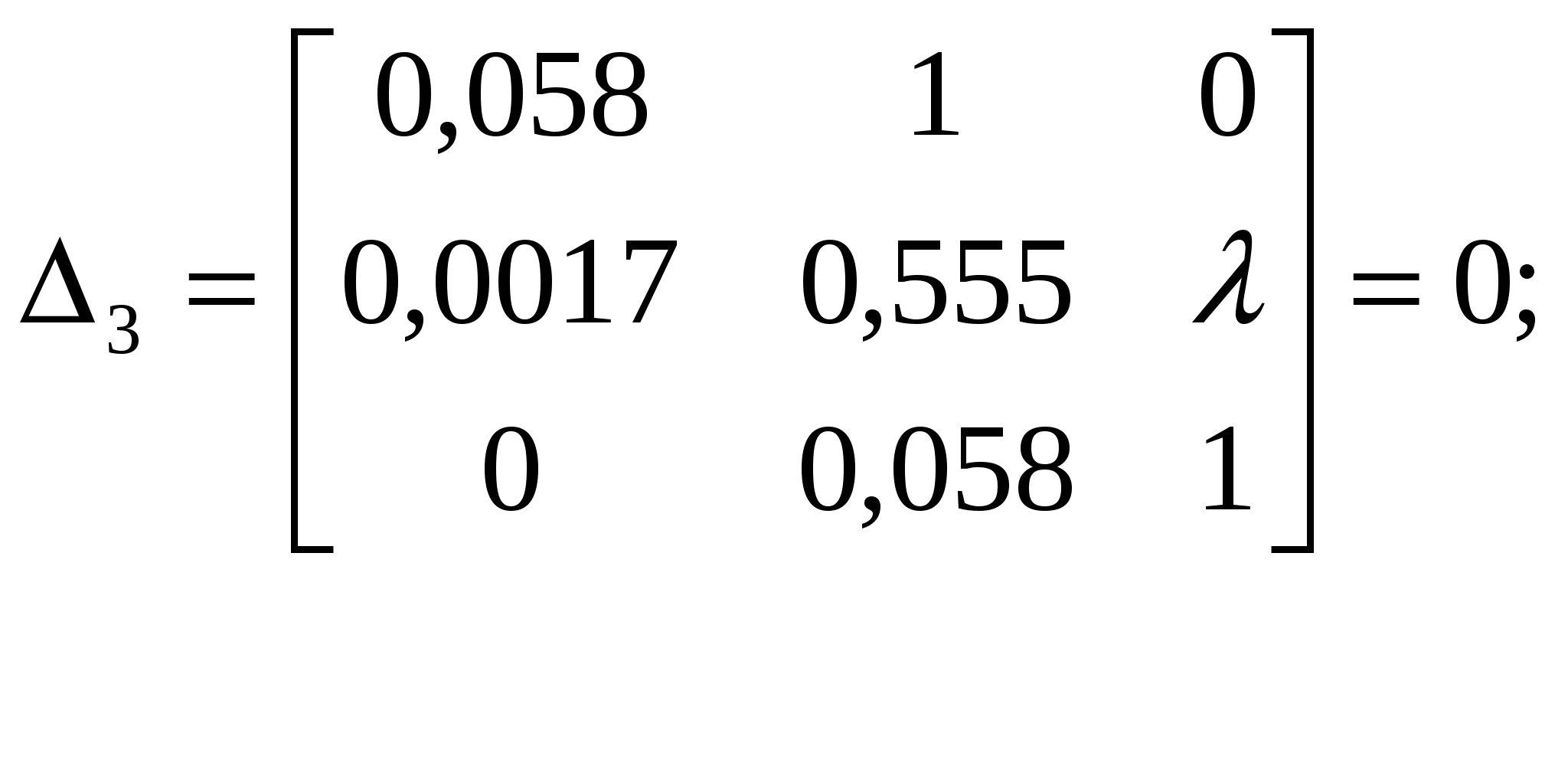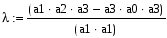

- критический коэффициент усиления


;

.
При данном коэффициенте усиления система будет находиться на границе устойчивости.