Вещественную частотную характеристику (рисунок 10) заменим мало отличающимися от кривой горизонтальными и наклонными прямолинейными участками, образующими с осью ординат трапеции. Действительная ВЧХ при этом будет представлена как алгебраическая сумма трапецеидальных частотных характеристик
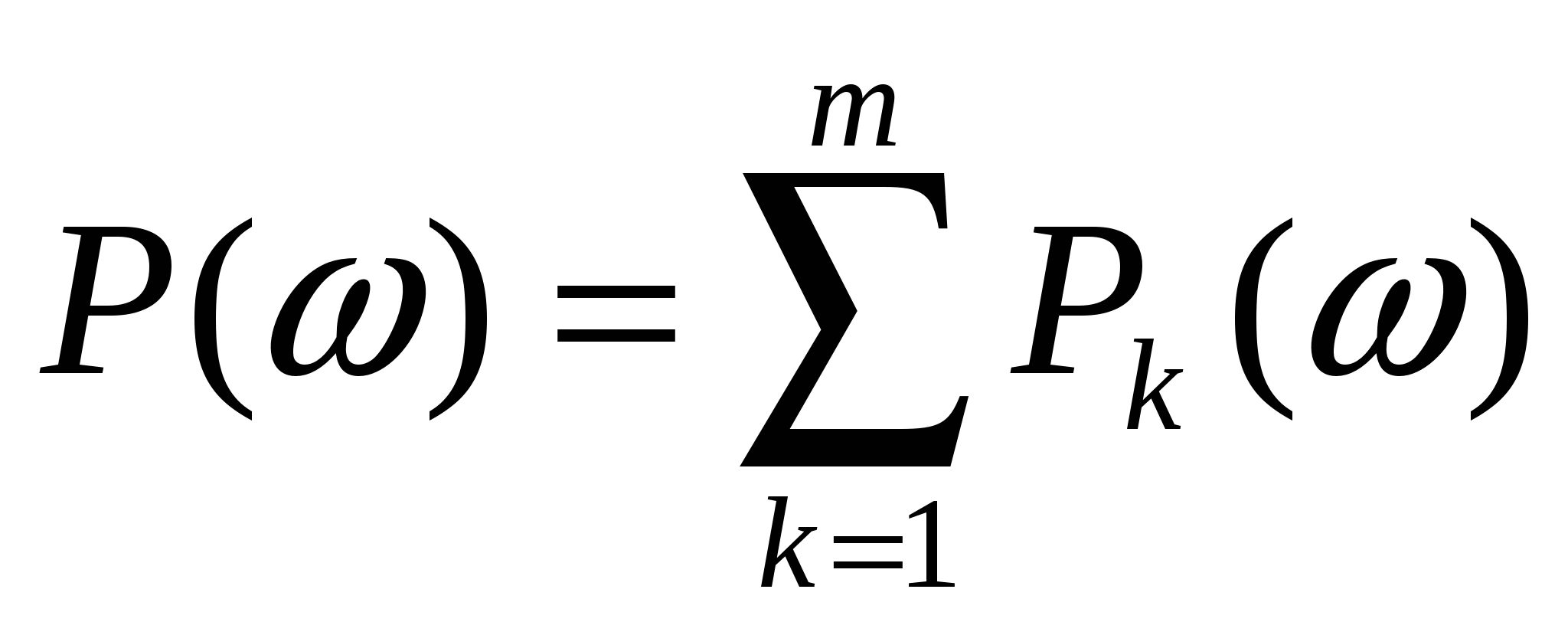 , (39) , (39)
где 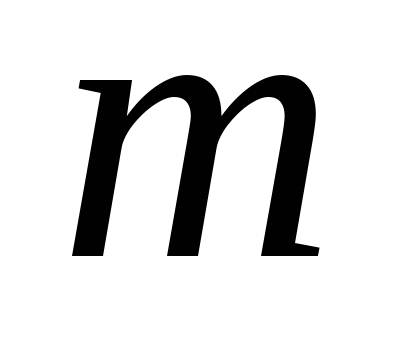 число трапеций. число трапеций.
Горизонтальные отрезки чертим в точках экстремумов. Первый отрезок должен начинаться из точки 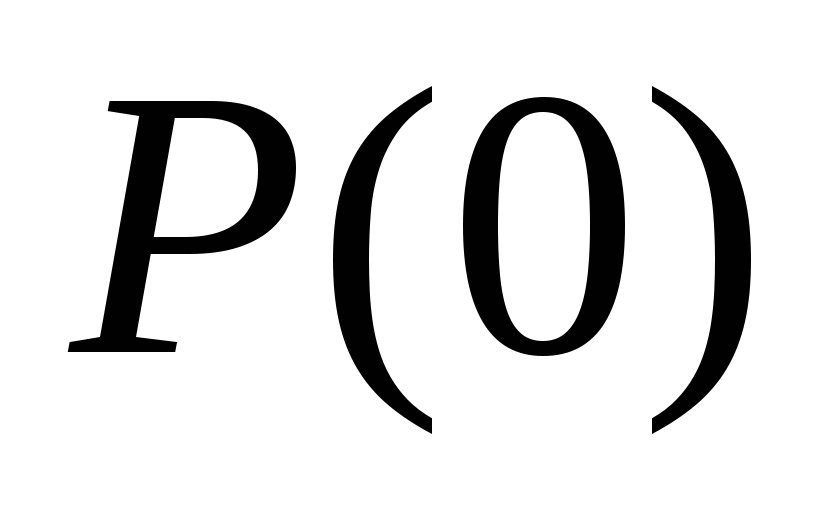 , т.к. эта точка определяет конечное значение переходной характеристики , т.к. эта точка определяет конечное значение переходной характеристики 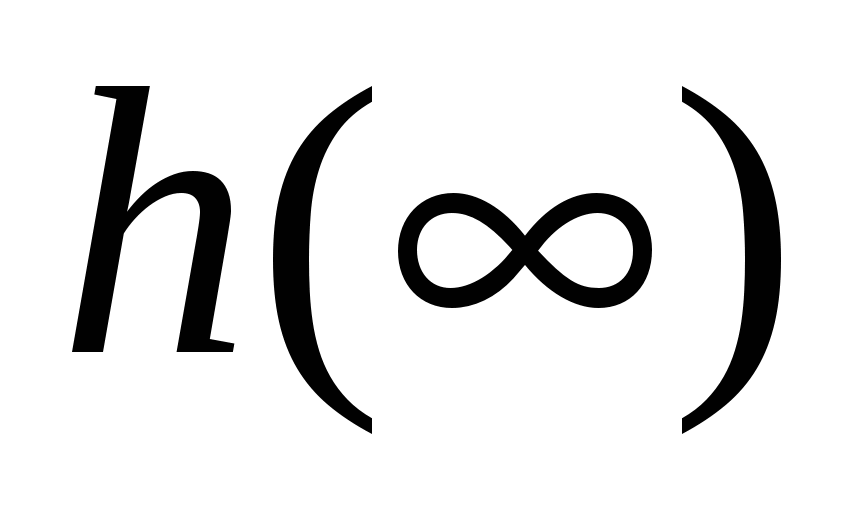 . Более тщательно нужно аппроксимировать начальный участок ВЧХ. Конечный участок с ординатами, меньшими по абсолютному значению, чем . Более тщательно нужно аппроксимировать начальный участок ВЧХ. Конечный участок с ординатами, меньшими по абсолютному значению, чем 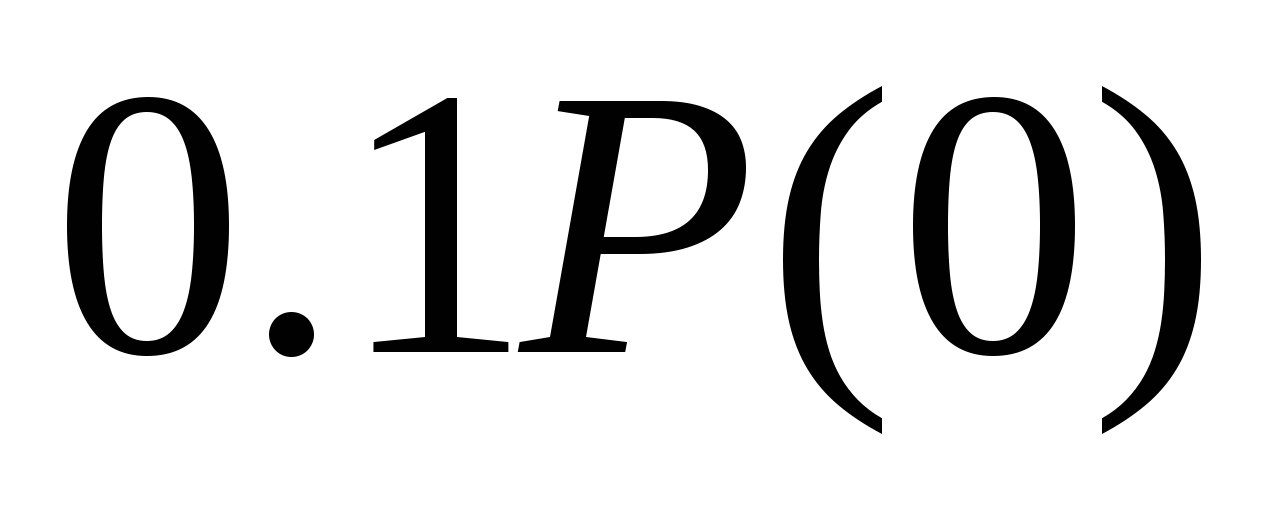 можно не принимать во внимание. можно не принимать во внимание.
Определим параметры трапеций.
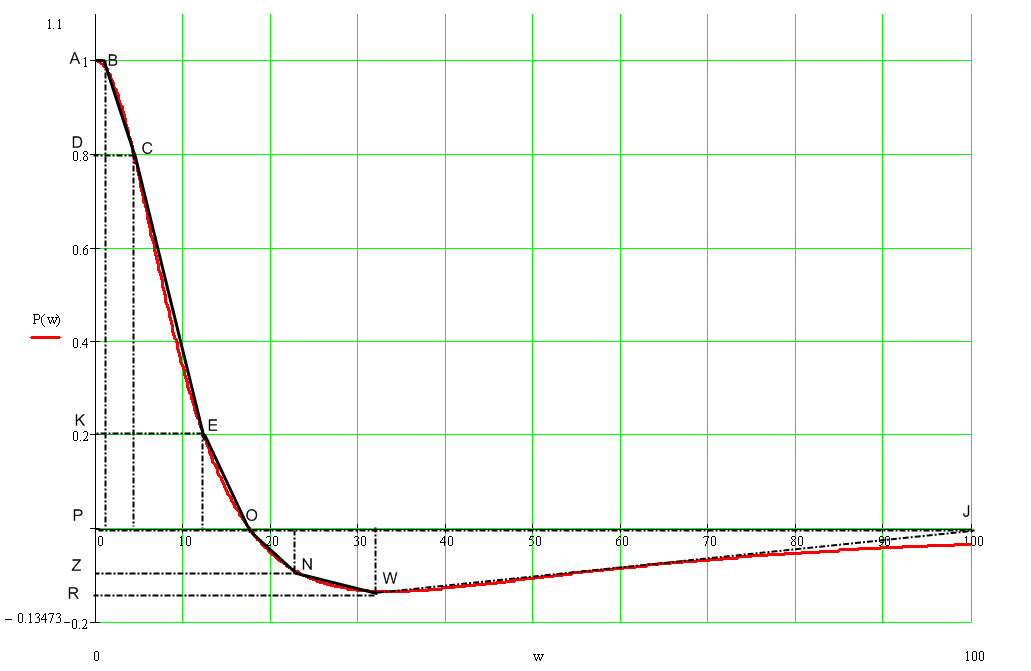
Рисунок 11 – Замена ВЧХ на трапеции
Из рисунка 11 находим параметры получившихся трапеций и заносим их в таблицу 3:
Таблица 3 – Параметры трапеций
|
ABCD
|
DCEK
|
KEOP
|
PONZ
|
ZNWR
|
RWJP
|
wd
|
1.3
|
4.8
|
13.5
|
18
|
23
|
32
|
wn
|
4.8
|
13.5
|
18
|
23
|
32
|
100
|
P
|
0.2
|
0.6
|
0.2
|
0.1
|
0.035
|
-0.135
|
x
|
0.25
|
0.35
|
0.7
|
0.8
|
0.75
|
0.3
|
По значениям  вычислим коэффициенты наклона вычислим коэффициенты наклона
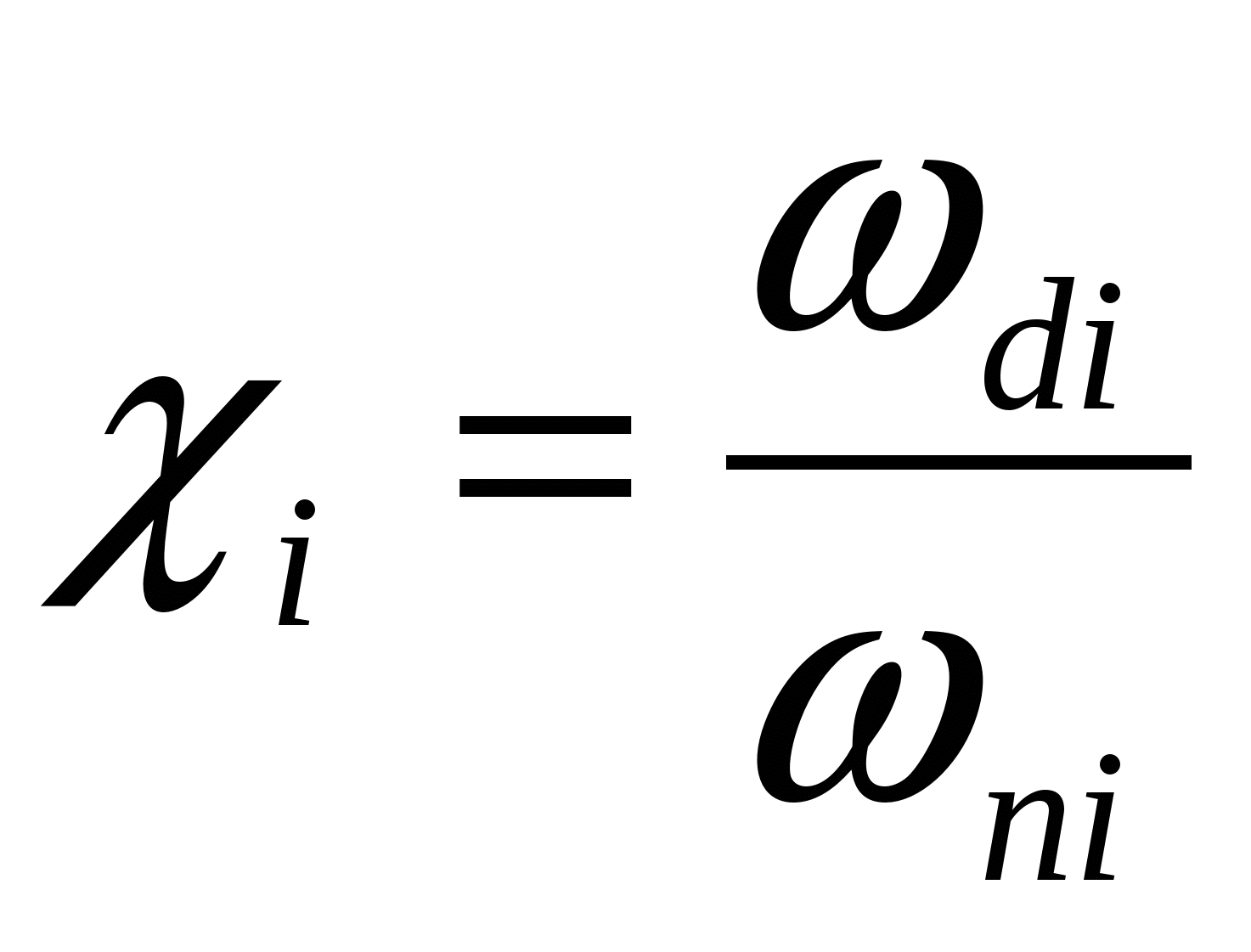 , (40) , (40)
и округлим их до ближайшего из значений 0; 0,05; 0,1; 0,15; … 0,95; 1.
Рассчитаем переходные процессы отдельно для каждой трапеции.
В таблице h-функций для каждой i-й трапеции отыскивается столбец, соответствующий значению коэффициента наклона 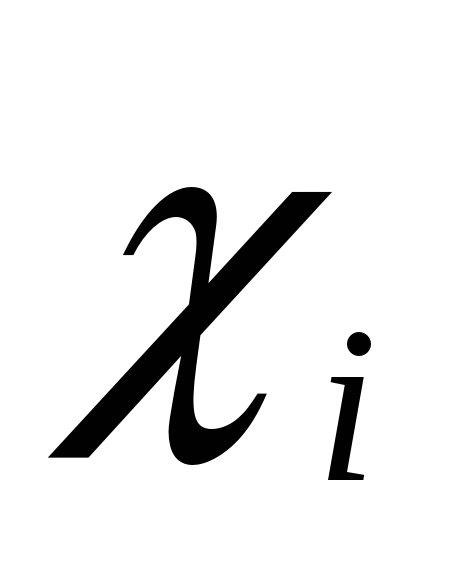 . Затем для ряда значений условного времени . Затем для ряда значений условного времени  выписывают соответствующие им значения выписывают соответствующие им значения 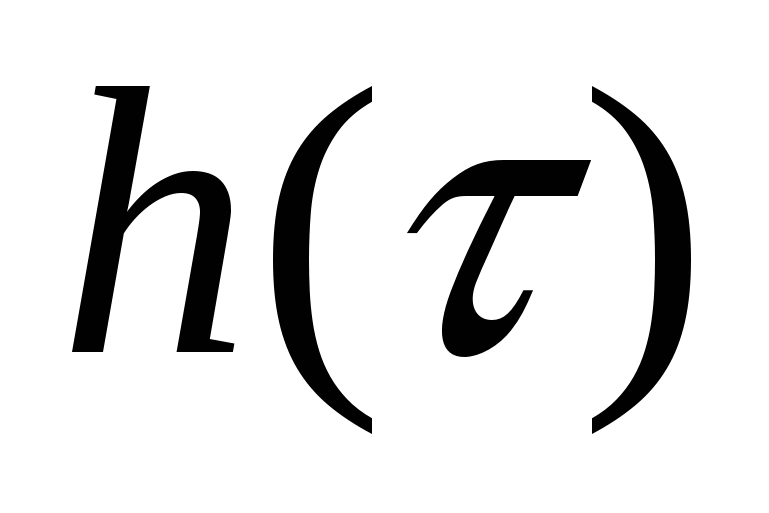 . По значениям . По значениям  и и 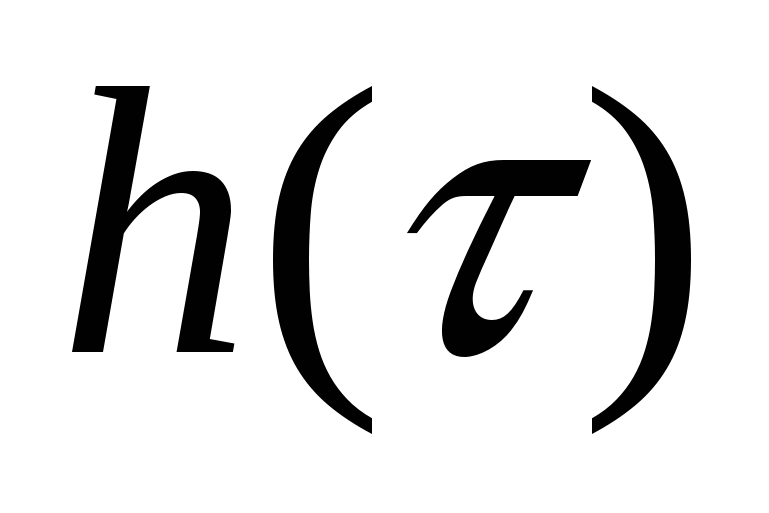 вычисляют значения действительного времени вычисляют значения действительного времени 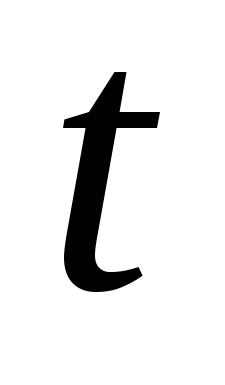 и составляющей переходной характеристики и составляющей переходной характеристики 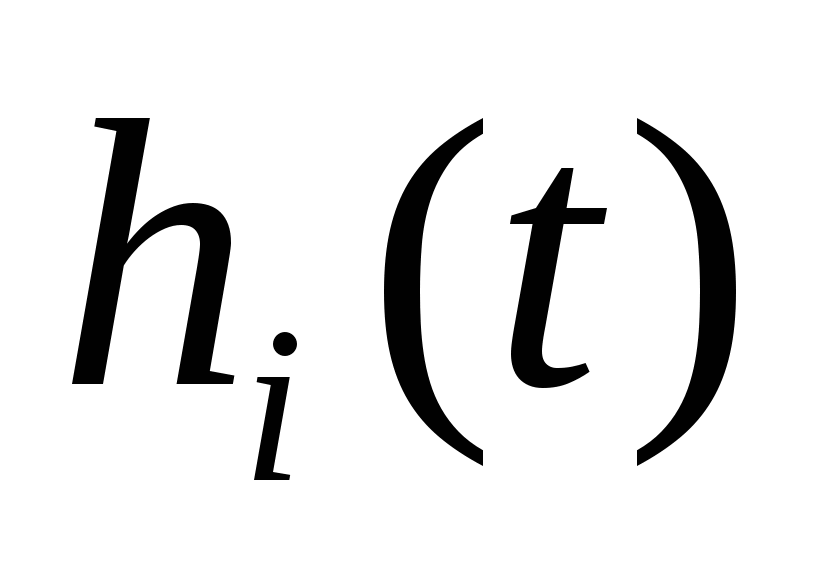 : :
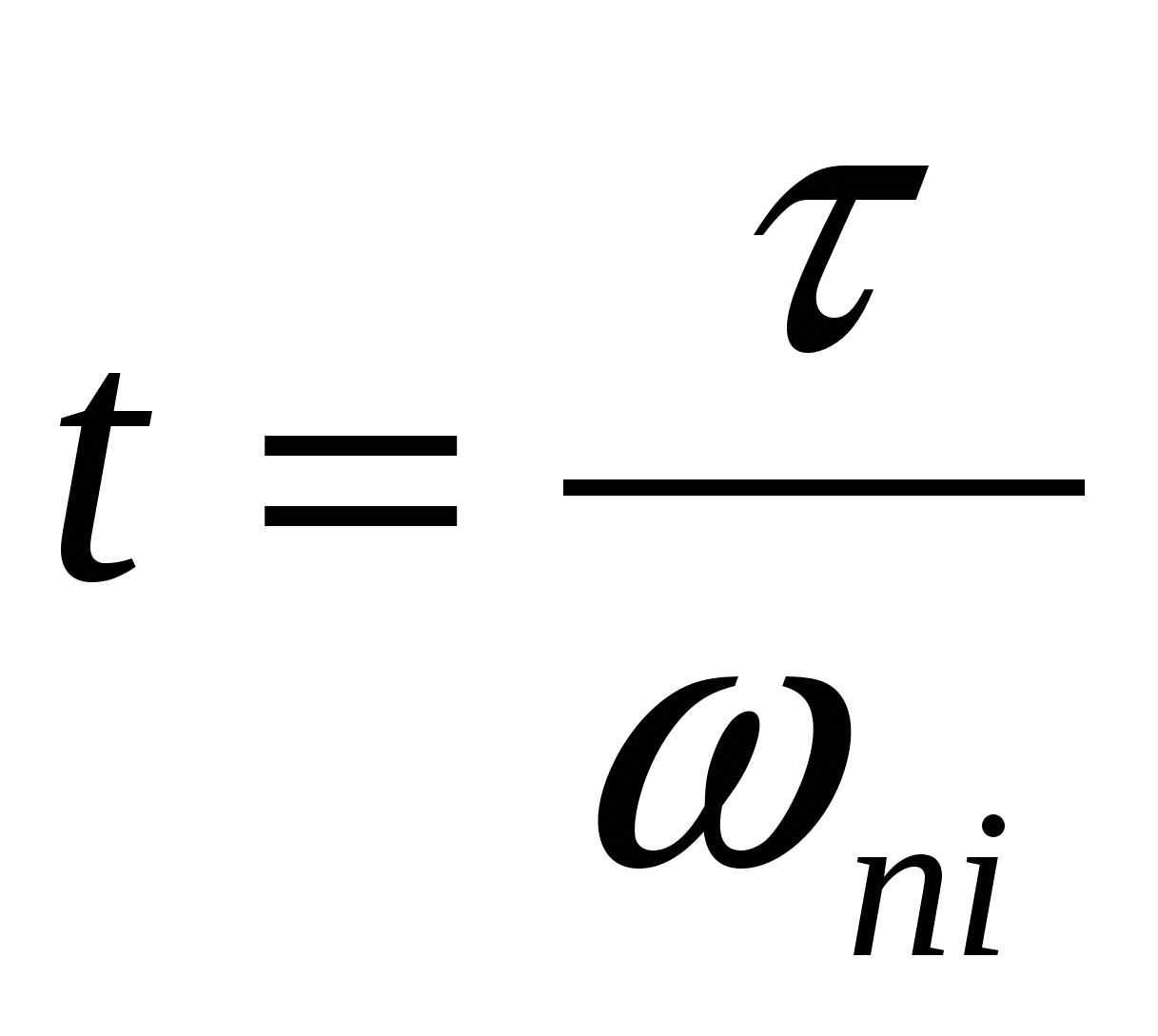 ; ; 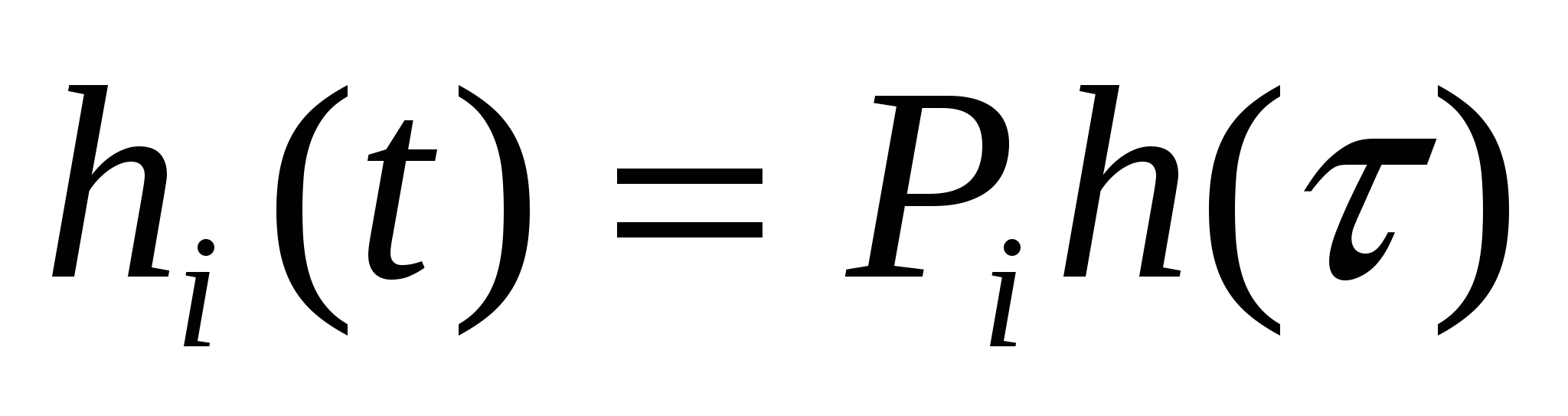 . (41) . (41)
Результаты оформим в таблице 4.
Таблица 4 – Расчет графиков составляющих переходной характеристики
Трапеция 1
|
Трапеция 2
|
Трапеция 3
|
ωd1=1,3;ωn1=4,8;χ=0,25;P1=0,2
|
ωd2=4,8;ωn2=13,5;χ=0,35;P2=0,6
|
ωd3=13,5;ωn3=18;χ=0,7;P3=0,2
|
τ
|
h1(τ)
|
t=τ/ωn1
|
h1(t)=h1(τ)*P1
|
τ
|
h2(τ)
|
t=τ/ωn2
|
h2(t)=h2(τ)*P2
|
τ
|
h3(τ)
|
t=τ/ωn3
|
h3(t)=h3(τ)*P3
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0,5
|
0,207
|
0,104167
|
0,0414
|
0,5
|
0,223
|
0,037037
|
0,1338
|
0,5
|
0,275
|
0,026316
|
0,055
|
1
|
0,401
|
0,208333
|
0,0802
|
1
|
0,432
|
0,074074
|
0,2592
|
1
|
0,534
|
0,052632
|
0,1068
|
1,5
|
0,594
|
0,3125
|
0,1188
|
1,5
|
0,617
|
0,111111
|
0,3702
|
1,5
|
0,758
|
0,078947
|
0,1516
|
2
|
0,681
|
0,416667
|
0,1362
|
2
|
0,786
|
0,148148
|
0,4716
|
2
|
0,938
|
0,105263
|
0,1876
|
2,5
|
0,839
|
0,520833
|
0,1678
|
2,5
|
0,938
|
0,185185
|
0,5628
|
2,5
|
1,06
|
0,131579
|
0,212
|
3
|
0,958
|
0,625
|
0,1916
|
3
|
1,013
|
0,222222
|
0,6078
|
3
|
1,42
|
0,157895
|
0,284
|
3,5
|
1,024
|
0,729167
|
0,2048
|
3,5
|
1,074
|
0,259259
|
0,6444
|
3,5
|
1,166
|
0,184211
|
0,2332
|
4
|
1,06
|
0,833333
|
0,212
|
4
|
1,107
|
0,296296
|
0,6642
|
4
|
1,161
|
0,210526
|
0,2322
|
4,5
|
1,08
|
0,9375
|
0,216
|
4,5
|
1,115
|
0,333333
|
0,669
|
4,5
|
1,127
|
0,236842
|
0,2254
|
5
|
1,087
|
1,041667
|
0,2174
|
5
|
1,112
|
0,37037
|
0,6672
|
5
|
1,069
|
0,263158
|
0,2138
|
5,5
|
1,083
|
1,145833
|
0,2166
|
5,5
|
1,095
|
0,407407
|
0,657
|
5,5
|
1,016
|
0,289474
|
0,2032
|
6
|
1,065
|
1,25
|
0,213
|
6
|
1,068
|
0,444444
|
0,6408
|
6
|
0,956
|
0,315789
|
0,1912
|
6,5
|
1,05
|
1,354167
|
0,21
|
6,5
|
1,043
|
0,481481
|
0,6258
|
6,5
|
0,936
|
0,342105
|
0,1872
|
7
|
1,037
|
1,458333
|
0,2074
|
7
|
1,023
|
0,518519
|
0,6138
|
7
|
0,917
|
0,368421
|
0,1834
|
7,5
|
1,025
|
1,5625
|
0,205
|
7,5
|
1,005
|
0,555556
|
0,603
|
7,5
|
0,911
|
0,394737
|
0,1822
|
8
|
1,021
|
1,666667
|
0,2042
|
8
|
0,995
|
0,592593
|
0,597
|
8
|
0,936
|
0,421053
|
0,1872
|
8,5
|
1,018
|
1,770833
|
0,2036
|
8,5
|
0,992
|
0,62963
|
0,5952
|
8,5
|
0,958
|
0,447368
|
0,1916
|
9
|
1,018
|
1,875
|
0,2036
|
9
|
0,992
|
0,666667
|
0,5952
|
9
|
0,99
|
0,473684
|
0,198
|
9,5
|
1,019
|
1,979167
|
0,2038
|
9,5
|
0,993
|
0,703704
|
0,5958
|
9,5
|
1,015
|
0,5
|
0,203
|
10
|
1,019
|
2,083333
|
0,2038
|
10
|
0,993
|
0,740741
|
0,5958
|
10
|
1,036
|
0,526316
|
0,2072
|
10,5
|
1,017
|
2,1875
|
0,2034
|
10,5
|
0,993
|
0,777778
|
0,5958
|
10,5
|
1,046
|
0,552632
|
0,2092
|
11
|
1,014
|
2,291667
|
0,2028
|
11
|
0,993
|
0,814815
|
0,5958
|
11
|
1,047
|
0,578947
|
0,2094
|
11,5
|
1,01
|
2,395833
|
0,202
|
11,5
|
0,991
|
0,851852
|
0,5946
|
11,5
|
1,043
|
0,605263
|
0,2086
|
12
|
1,004
|
2,5
|
0,2008
|
12
|
0,988
|
0,888889
|
0,5928
|
12
|
1,025
|
0,631579
|
0,205
|
12,5
|
0,999
|
2,604167
|
0,1998
|
12,5
|
0,986
|
0,925926
|
0,5916
|
12,5
|
1,01
|
0,657895
|
0,202
|
13
|
0,994
|
2,708333
|
0,1988
|
13
|
0,985
|
0,962963
|
0,591
|
13
|
0,993
|
0,684211
|
0,1986
|
13,5
|
0,99
|
2,8125
|
0,198
|
13,5
|
0,984
|
1
|
0,5904
|
13,5
|
0,982
|
0,710526
|
0,1964
|
14
|
0,988
|
2,916667
|
0,1976
|
14
|
0,985
|
1,037037
|
0,591
|
14
|
0,974
|
0,736842
|
0,1948
|
14,5
|
0,987
|
3,020833
|
0,1974
|
14,5
|
0,988
|
1,074074
|
0,5928
|
14,5
|
0,97
|
0,763158
|
0,194
|
15
|
0,988
|
3,125
|
0,1976
|
15
|
0,991
|
1,111111
|
0,5946
|
15
|
0,976
|
0,789474
|
0,1952
|
15,5
|
0,989
|
3,229167
|
0,1978
|
15,5
|
0,996
|
1,148148
|
0,5976
|
15,5
|
0,984
|
0,815789
|
0,1968
|
16
|
0,991
|
3,333333
|
0,1982
|
16
|
0,998
|
1,185185
|
0,5988
|
16
|
0,983
|
0,842105
|
0,1966
|
16,5
|
0,993
|
3,4375
|
0,1986
|
16,5
|
1,002
|
1,222222
|
0,6012
|
16,5
|
1,001
|
0,868421
|
0,2002
|
17
|
0,994
|
3,541667
|
0,1988
|
17
|
1,005
|
1,259259
|
0,603
|
17
|
1,008
|
0,894737
|
0,2016
|
17,5
|
0,994
|
3,645833
|
0,1988
|
17,5
|
1,006
|
1,296296
|
0,6036
|
17,5
|
1,012
|
0,921053
|
0,2024
|
18
|
0,995
|
3,75
|
0,199
|
18
|
1,008
|
1,333333
|
0,6048
|
18
|
1,014
|
0,947368
|
0,2028
|
18,5
|
0,995
|
3,854167
|
0,199
|
18,5
|
1,007
|
1,37037
|
0,6042
|
18,5
|
1,012
|
0,973684
|
0,2024
|
19
|
0,995
|
3,958333
|
0,199
|
19
|
1,006
|
1,407407
|
0,6036
|
19
|
1,009
|
1
|
0,2018
|
19,5
|
0,995
|
4,0625
|
0,199
|
19,5
|
1,005
|
1,444444
|
0,603
|
19,5
|
1,005
|
1,026316
|
0,201
|
20
|
0,995
|
4,166667
|
0,199
|
20
|
1,005
|
1,481481
|
0,603
|
20
|
1,001
|
1,052632
|
0,2002
|
20,5
|
0,996
|
4,270833
|
0,1992
|
20,5
|
1,004
|
1,518519
|
0,6024
|
20,5
|
0,996
|
1,078947
|
0,1992
|
21
|
0,997
|
4,375
|
0,1994
|
21
|
1,004
|
1,555556
|
0,6024
|
21
|
0,993
|
1,105263
|
0,1986
|
21,5
|
0,999
|
4,479167
|
0,1998
|
21,5
|
1,004
|
1,592593
|
0,6024
|
21,5
|
0,992
|
1,131579
|
0,1984
|
22
|
1
|
4,583333
|
0,2
|
22
|
1,004
|
1,62963
|
0,6024
|
22
|
0,991
|
1,157895
|
0,1982
|
22,5
|
1,002
|
4,6875
|
0,2004
|
22,5
|
1,004
|
1,666667
|
0,6024
|
22,5
|
0,992
|
1,184211
|
0,1984
|
23
|
1,004
|
4,791667
|
0,2008
|
23
|
1,003
|
1,703704
|
0,6018
|
23
|
0,994
|
1,210526
|
0,1988
|
23,5
|
1,004
|
4,895833
|
0,2008
|
23,5
|
1,003
|
1,740741
|
0,6018
|
23,5
|
0,997
|
1,236842
|
0,1994
|
24
|
1,005
|
5
|
0,201
|
24
|
1,002
|
1,777778
|
0,6012
|
24
|
1
|
1,263158
|
0,2
|
24,5
|
1,005
|
5,104167
|
0,201
|
24,5
|
1,001
|
1,814815
|
0,6006
|
24,5
|
1,002
|
1,289474
|
0,2004
|
25
|
1,005
|
5,208333
|
0,201
|
25
|
1
|
1,851852
|
0,6
|
25
|
1,003
|
1,315789
|
0,2006
|
25,5
|
1,004
|
5,3125
|
0,2008
|
25,5
|
0,998
|
1,888889
|
0,5988
|
25,5
|
1,004
|
1,342105
|
0,2008
|
26
|
1,004
|
5,416667
|
0,2008
|
26
|
0,997
|
1,925926
|
0,5982
|
26
|
1,004
|
1,368421
|
0,2008
| |
 Скачать 1.41 Mb.
Скачать 1.41 Mb.
