Анализ таблиц истинности логических выражений
 Скачать 2.43 Mb. Скачать 2.43 Mb.
|
Ещё пример задания:Р-08. Дан фрагмент таблицы истинности выражения F.
Какое выражение соответствует F? 1) (x2 x1) ¬x3 x4 ¬x5 x6 ¬x7 x8 2) (x2 x1) ¬x3 x4 ¬x5 x6 ¬x7 x8 3) ¬(x2 x1) x3 ¬x4 x5 ¬x6 x7 ¬x8 4) (x2 x1) x3 ¬x4 x5 ¬x6 x7 ¬x8 Решение: перепишем выражение в более простой форме, заменив «И» () на умножение и «ИЛИ» () на сложение: 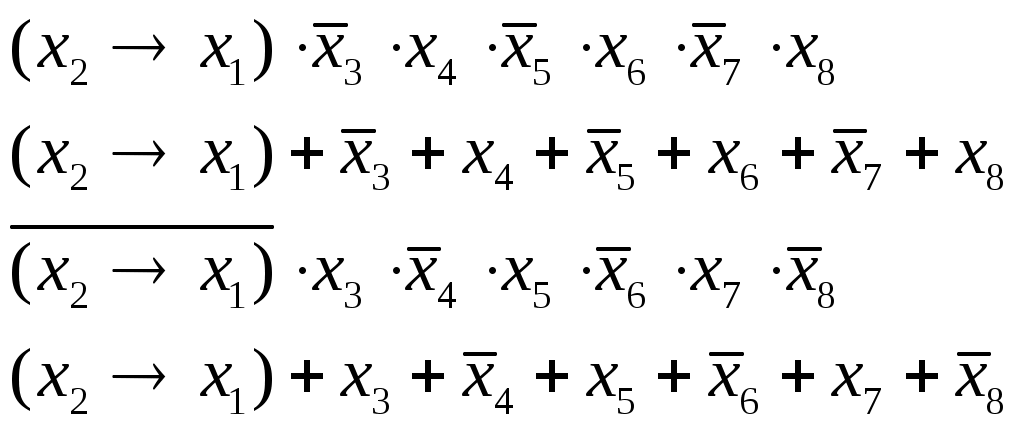 в этом задании среди значений функции только одна единица, как у операции «И», это намекает на то, что нужно искать правильный ответ среди вариантов, содержащих «И», «НЕ» и импликацию (это варианты 1 и 3) действительно, вариант 2 исключён, потому что при x4=1 во второй строке получаем 1, а не 0 аналогично, вариант 4 исключён, потому что при x5=1 в первой строке получаем 1, а не 0 итак, остаются варианты 1 и 3; вариант 1 не подходит, потому что при x6=0 в третьей строке получаем 0, а не 1 проверяем подробно вариант 3, он подходит во всех строчках Ответ: 3. Ещё пример задания:Р-07. Дан фрагмент таблицы истинности выражения F.
Какое выражение соответствует F? 1) (x1 x2) (x3 x4) (x5 x6) 2) (x1 x3) (x3 x5) (x5 x1) 3) (x2 x4) (x4 x6) (x6 x2) 4) (x1 x4) (x2 x5) (x3 x6) Решение: во-первых, обратим внимание, что в столбце F – все нули, то есть, при всех рассмотренных наборах x1, …, x6 функция ложна перепишем предложенные варианты в более простых обозначениях: x1x2 + x3x4 + x5x6 x1x3 + x3x5 + x5x1 x2x4 + x4x5 + x6x2 x1x4 + x2x5 + x3x6 это суммы произведений, поэтому для того, чтобы функция была равна 0, необходимо, чтобы все произведения были равны 0 по таблице смотрим, какие произведения равны 1: 1-я строка: x2x5, x2x6 и x5x6 2-я строка: x3x6 3-я строка: x2x4, x2x6 и x4x6 таким образом, нужно выбрать функцию, где эти произведения не встречаются; отметим их: x1x2 + x3x4 + x5x6 x1x3 + x3x5 + x5x1 x2x4+ x4x5 + x6x2 x1x4 + x2x5+ x3x6 единственная функция, где нет ни одного «запрещённого» произведения – это функция 2 Ответ: 2. |
