Анализ видов и последствий отказов
 Скачать 1.94 Mb. Скачать 1.94 Mb.
|
|
Обычно при наличии количественных данных они. как правило, связаны с отказами объекта или процесса в целом, а не с конкретными видами отказов элементов. Оценка вероятности вида отказа может быть получена путем декомпозиции вероятности отказа объекта в целом на вероятности возможных видов отказов. Кроме того, может быть сделана корректировка для представления вероятности того, что вид отказа приведет к конкретным последствиям (обычно определенной значимости). Примечание — Если в качестве показателя используют интенсивность отказов, то. если не указано иное, этот подход предполагает, что интенсивность отказов постоянна и. следовательно, это может быть неприемле- мым в некоторых ситуациях. Кроме того, хотя интенсивность отказов объекта может быть получена из конкретных данных, условная вероятность видов отказов и вероятность того, что конкретный уровень последствий соответ- ствует данному виду отказа, также часто получают из другого набора источников данных или на основе выводов и заключений. Если используют диапазоны/категории вероятности, описания могут быть сделаны с использованием эм- пирических данных, экспертных заключений команды разработчиков или на основе других источников данных. Важно, чтобы была использована соответствующая шкала, позволяющая применять точную оценку относительной частоты видов отказов и ее соответствие имеющимся данным. Чтобы облегчить точное и согласованное применение, следует учитывать следующее. При использовании количественных показателей, таких как вероятность или частота, единицы измерений должны быть четко указаны. Пример 1 — Если используют значение е процентах, то указывают величину, относительно ко- торой определяют процент, например процент объектов, отказавших в течение вода. Количественные пояснения описания категории, соответствующей диапазону вероятностей, ожидаемых для данного применения, должно быть приведено (по возможности) для общего понимания. Пример 2 — Для технических систем с высокой безотказностью частота вида отказа элемента может составлять один отказ за несколько лет, а для менее надежных систем частота вида отказа объекта может составлять несколько отказов за год. Описание вероятности для редких отказов должно быть реалисти'ыым и применимо к наихудшему случаю. Назначение критичности с использованием матрицы или графика Общие положения Для обеспечения возможности определения ранга критичности взаимосвязь параметров критичности может быть представлена несколькими способами. Вероятность и последствия отказа могут быть представлены с по- мощью непрерывных шкал или категорий, а затек! объединены для визуального представления в форме графика или матрицы. График или матрицу критичности затем используют для определения приоритетности обработки. Значение каждого рэнга критичности и его связь с соответствующей обработкой необходимо обсудить и со- гласовать с заинтересованными сторонами до проведения анализа при планировании FMEA. Это дает четкое и однозначное понимание способа обработки вида отказа и возможного влияния такого решения на бизнес. Невоз- можность выполнения этого сводит на нет значение анализа критичности и может привести к существенным затра- там времени и средств из-за излишних действий или неадекватной обработки отказов. Количество необходимых рангов критичности определяют требования организации и область применения анализа. Матрица критичности Анализ матрицы критичности формирует меру значимости путем объединения значений вероятности и по- следствий. Матрицу критичности таюке называют матрицей риска. Значения по каждому параметру формируют в виде матрицы, а ранг критичности присваивают каждой ячейке матрицы. Ранг критичности может быть связан с уровнем обработки, которую применяют к соответствующему виду отказа. Для видов отказов с низким рангом об- работка может включать «бездействие». На рисунке В.1 показан пример качественной матрицы критичности Значимость последствий
Рисунок ВЛ — Пример качественной матрицы критичности Примечание 1 — Примером четырех уровней категорий критичности (как на рисунке ВЛ) являются: Категория X: «Недопустимый риск»; Категория 1: «Нежелательный риск»; Категория 2: «Приемлемый риск»; Категория 3: «Несущественный риск». В некоторых случаях вид отказа может привести к ряду различных последствий в зависимости от обстоя- тельств. В этом случае должны быть указаны последствия, которым соответствует вероятность. В такой ситуации полезно рассмотреть критичность нескольких возможных последствий. В матрице на рисунке В.1 риск, соответствующий каждой категории критичности, возрастает от нижнего пра- вого угла матрицы до верхнего левого. Однако обработка каждого вида отказа зависит только от классификации критичности (то есть цвета или кода критичности), а не от положения ячейси матрицы. Примечание 2 — Использование термина «приемлемый риск» не означает, что дальнейшая обработка является нежелательной. Матрица, представленная на рисунке В.1. является только примером, ее не следует рассматривать какобяза- гельную форму матрицы критичности. Фактическая форма матрицы зависит от конкретной ситуации. Если количе- ство диапазонов вероятности, категорий значимости и последствий различно, то форма матрицы будет отличаться от представленной на рисунке В.1. Если критичность, соответствующая комбинациям вероятности и значимости последствий, отличается от приведенной на рисунке В.1. кодирование также будет иным. Матрица не обязательно ограничена двумя измерениями, ее можно расширить, добавив третий параметр или. теоретически, столько других параметров, сколько требуется. Однако сложность и усилия, необходимые для описания правильной и управляемой многомерной матрицы, могут быть значительными и неэффективными, по- скольку каждая комбинация параметров требует оценки. Матрица критичности должна быть выведена так, чтобы видам отказов с одинаковой значимостью соответ- ствовали одинаковое значение критичности и одинаковая обработка. Кроме того, если категории значимости по- следствий или вероятности основаны на количественных или полухоличественных оценках, следует рассмотреть вопрос о приемлемости различных вариантов обработки, применяемых к видам отказов по обе стороны от границы критичности. График критичности На рисунке В.2 показаны примеры простых графиков вероятности и последствий с назначенными рангами критичности. В этом случае как вероятность, так и значимость последствий представляют собой непрерывные количественные шкалы. Границы между диапазонами не обязательно должны быть прямыми (пример В) или кривыми (пример А). В соответствии с требованиями обработки выявленных видов отказов граница может быть ступенчатой (пример С) или комбинацией прямых и кривых ганий. Примечание 1 — В примере В границы диапазонов представляют собой линии одинакового уровня ри- ска. Если для вероятности и последствий использована линейная шкала, границы будут кривыми. Если использо- ваны логарифмические шкалы, границы будут прямыми. 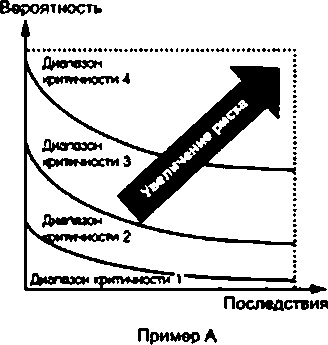 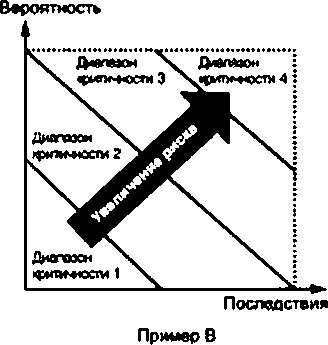 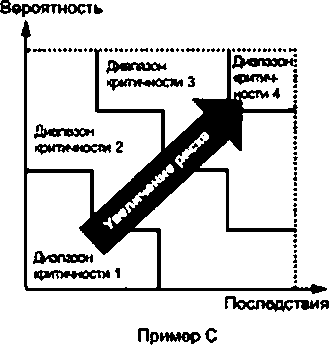 Рисунок В.2 — Примеры графиков критичности Примечание 2 — Если для вероятности ислогъзованз линейная шкала, вероятность может принимать значение, равное нулю. Это может привести к ошибочным рангам критичности для высоких последствий и низкой вероятности отказов. На практике гладкие границы диапазонов имеют смысл только в том случае, если вероятность может быть выражена количественно, а последствия отказов изменяются непрерывно (например, финансовые последствия) и могут быть полностью определены. График критичности не обязатегъно должен быть ограничен двумя параметрами, при необходимости он мо- жет быть расширен до трех параметров. Однако сложность и усилия, необходимые для формирования правильных границ, могут быть змачигетъными и неэффективными с точки зрения затрат. В случаях, когда для значимости последствий может быть использована количественная шкала, имеющая различные значения или диапазоны значений, график критичности все еще применим, но границы значений кри- тичности почти наверняка будут ступенчатыми. Это приводит к аналогичному представлению в матрице критич- ности. |
