Рисунок 13
Г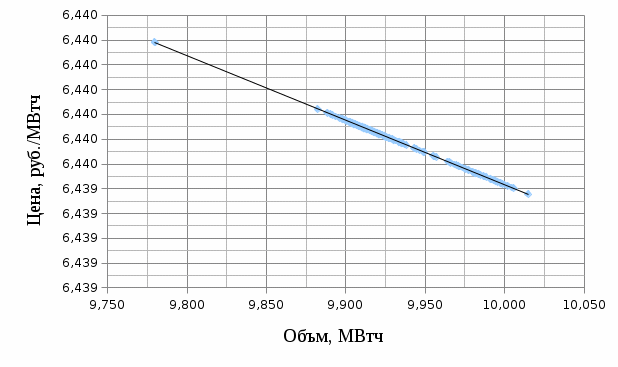 рафик равновесных точек, общая модель рафик равновесных точек, общая модель
В данной модели коэффициент детерминации равен всего 2,5%, на столько процентов вариация равновесных объёмов объясняется вариацией равновесных цен.
Далее осуществим проверку гипотезы о значимости регрессора, с помощью т – статистики. Путь гипотеза  – регрессор не значим: – регрессор не значим:
Задаем уровень значимости: α= 0,1
Найдем t наблюдаемое по формуле (3): 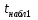 = 0,233, = 0,233,  = 1,333 = 1,333
Найдем t критическое по формуле (4): 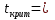 1,653 1,653
Сравниваем: 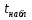 < <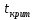 => гипотеза => гипотеза  – принимается, для – принимается, для 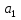 , ,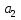 при α= 0,1 => регрессоры при α= 0,1 => регрессоры 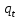 , ,  – не значимы. – не значимы.
Последний шаг в анализе – это проверка гипотезы о значимости модели. Гипотеза  : : 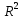 =0 – модель не значима: =0 – модель не значима:
Задаем уровень значимости: α= 0,1
Находим эмпирическое значение по формуле (6): 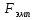 = 2,347 = 2,347
Находим критическое значение по формуле (7): 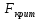 = 2,331 = 2,331
Сравниваем: 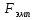 > >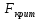 => =>  - отвергается, логарифмическая модель с - отвергается, логарифмическая модель с  значима при α= 0,1. значима при α= 0,1.
Эластичность при 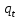 равна 0,681, а при равна 0,681, а при  равна -3,869. То есть изменение объема в данный период не оказывает особого влияния на изменение равновесных цен электроэнергии, а изменение объема в предыдущем периоде оказывает влияние на изменение равновесных цен электроэнергии. равна -3,869. То есть изменение объема в данный период не оказывает особого влияния на изменение равновесных цен электроэнергии, а изменение объема в предыдущем периоде оказывает влияние на изменение равновесных цен электроэнергии.
Таким образом, анализ показал, что логарифмическая модель с  значима, а также статистическую не значимость параметра уравнения регрессии. Однако, теснота логарифмической связи не достаточна, чтобы признать данную модель приемлемой, а тем более хорошей. значима, а также статистическую не значимость параметра уравнения регрессии. Однако, теснота логарифмической связи не достаточна, чтобы признать данную модель приемлемой, а тем более хорошей.
Подведем итог по летнему периоду. В таблице 7 представлены все получившиеся результаты.
Таблица 7
Сводные данные за летний период
Линейная модель
|
|
0
|
1
|
2
|
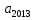
|
-539,129
|
0,066**
|
-
|
|
(434,496)
|
(-0,021)
|
-
|
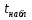
|
-
|
3,131
|
-
|
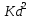
|
0,116
|
df
|
75
|
F
|
модель значима *** 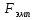 > >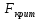
|
Продолжение табл. 7
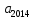
|
1583,459
|
-0,052*
|
-
|
|
568,487
|
0,027
|
-
|
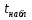
|
-
|
1,88
|
-
|
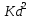
|
0,046
|
df
|
74
|
F
|
модель значима * 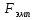 > >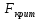
|
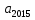
|
139,45
|
0,022*
|
-
|
|
(997,78)
|
(0,049)
|
-
|
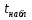
|
-
|
0,447
|
-
|
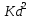
|
0,006
|
df
|
34
|
F
|
модель не значима* 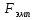 < <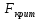
|
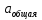
|
869,012
|
-0,01*
|
-
|
|
(439,508)
|
(0,021)
|
-
|
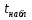
|
-
|
0,492
|
-
|
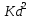
|
0,001
|
df
|
187
|
F
|
модель не значима* 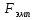 < <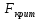
|
Логарифмическая модель
|
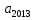
|
-10,287
|
1,71**
|
-
|
|
(5,032)
|
(0,507)
|
-
|
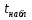
|
-
|
3,374
|
-
|
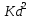
|
0,132
|
df
|
75
|
F
|
модель значима *** 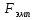 > >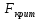
|
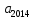
|
63,962
|
-5,829**
|
-
|
|
(33,825)
|
(3,403)
|
-
|
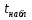
|
-
|
19,838
|
-
|
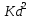
|
0,038
|
df
|
74
|
F
|
модель значима *** 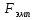 > >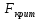
|
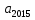
|
-0,026
|
0,641*
|
-
|
|
(20,452)
|
(2,06)
|
-
|
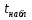
|
-
|
0,311
|
-
|
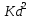
|
0,003
|
df
|
34
|
F
|
модель не значима* 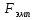 < <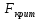
|
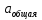
|
6,499
|
-0,004*
|
-
| |
 Скачать 0.5 Mb.
Скачать 0.5 Mb. рафик равновесных точек, общая модель
рафик равновесных точек, общая модель