Диплом11. Анализ взаимосвязи равновесных цен и объемов на основе заявок на оптовый рынок
 Скачать 0.5 Mb.
|
|
Глава 3 Создание и построение эконометрических моделей с целью оценки ценовой эластичности В данной главе речь пойдет: об описание моделей; об применяемых формулах; об анализе получившихся моделей с помощью т-статистики. 3.1 Описание моделей Мною было рассмотрено пять вариантов моделей: линейная; логарифмическая; линейная модель с  ;логарифмическая модель с ;модель для определения долгосрочной эластичности. Линейная модель имеет вид: 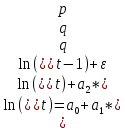 , где p - цена на электроэнергию, t - момент времени,  - параметры модели, q - объем электроэнергии, ε – остатки. Логарифмическая модель имеет вид:  . Линейная модель с имеет вид:  , где – объем электроэнергии в предыдущий период. Логарифмическая модель с имеет вид:  . Модель для определения долгосрочной эластичности имеет вид:  .Для каждой модели найдем: стандартные ошибки коэффициентов, с помощью которых определим, насколько расчетные значения в среднем отклоняются от фактических значений; коэффициент детерминации, с его помощью определим, насколько процентов вариация равновесных объёмов объясняется вариацией равновесных цен; определим значимость коэффициентов с помощью т – статистики. Kd - коэффициент детерминации. предполагается, что коэффициент детерминации должен быть хотя бы не меньше 50%. Модели с коэффициентом детерминации выше 80% можно признать достаточно хорошими. Так же эти модели описывают две гипотезы: гипотеза о значимости регрессора; гипотеза о значимости модели. В данной работе для создания моделей были найдены точки пересечения спроса и предложения в пиковые часы в двух периодах: с 20 мая по 10 сентября; с 20 ноября по 10 марта. В первом периоде количество данных значительно меньше, чем во втором, это связано с тем, что за пиковые часы в период с 20 мая по 10 сентября я брала один пиковый час (по данным генераторов) и только в рабочие дни. В период с 20 ноября по 10 марта за пиковые часы принято время с 4:00 до 7:00 утра и с 13:00 до 16:00 вечера, как в рабочие, так и в выходные дни. Как говорилось ранее в работе, данные были взять с 1 января 2013 года по 31 декабря 2015 года. Следовательно, в первом периоде получилось четыре варианта модели (2013 г., 2014 г., 2015 г., общая). Во втором периоде пять вариантов модели (2013 г., 2013-2014 гг., 2014-2015 гг., 2015 г., общая). В каждой модели была проведена корректировка цена на индекс потребительских цен прил. 1. Все параметры модели находились в программе Excel с помощью формулы (1) =ЛИНЕЙН (  . (1)Так же была найдена новая цена, после определения параметров модели, путем подстановки необходимого значения объема электроэнергии в определенный момент в модель, и остатки по формуле (2).  , (2)где ε - остатки,  - первоначальная цена,  - новая цена.3.2 Анализ моделей с помощью т-статистики Т-статистика позволяет определить, подходит ли каждый коэффициент наклона для оценки стоимости электроэнергии. Для этого необходимо рассчитать t- наблюдаемое значение и t- критическое значение. Наблюдаемое t - значение находится по формуле  , (3)где  -стандартные значения шибок для параметров модели. Это значение считается автоматически и находится на второй строке в ответе при расчете формулы (1). Критическое t - значение находится в программе Excel с помощью формулы  , (4)где α – уровень значимости, df – степени свободы. Степени свободы находятся по формуле  , (5)где n – число наблюдений, k- число объясняющих параметров. Если t-наблюдаемо больше чем t-критическое, следовательно, коэффициент наклона можно использовать для оценки стоимости электроэнергии. 3.3 Эконометрические модели в летний период Летним периодом мы будем называть период с 20 мая по 10 сентября. Этот период характеризуется малым количеством фирм и не большой конкуренцией. 3.3.1 Модель В 2013 году после нахождения всех точек пересечения, получилось семьдесят семь значений. По формуле (1) параметры модели равны:  = -539,129,  = 0,066. Следовательно, модель выглядит следующим образом:  . С помощью этой модели находим новую цену и остатки (табл.5). Так же по первоначальным данным строим график и проводим линейный тренд. Так как коэффициент наклона в данном случае положителен, то и линия тренда имеет положительный наклон. Это наглядно видно на рис. 12. Таблица 5 Исходные данные, новая цена и остатки, 2013 год
Рисунок 12 Г 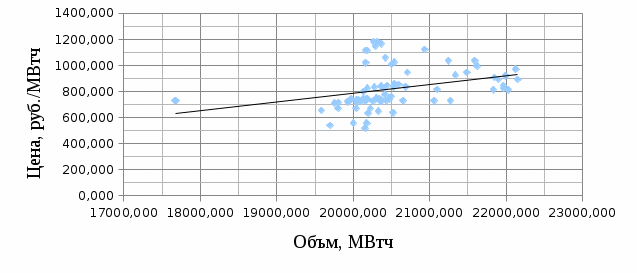 рафик равновесных точек, 2013 годВ данной модели коэффициент детерминации равен всего 11,6%, на столько процентов вариация равновесных объёмов объясняется вариацией равновесных цен. Далее осуществим проверку гипотезы о значимости регрессора, с помощью т – статистики. Путь гипотеза  – регрессор не значим:Задаем уровень значимости: α= 0,05 Найдем t наблюдаемое по формуле (3):  = 3,131Найдем t критическое по формуле (4):  1,992 Сравниваем: > => гипотеза – отвергается, для при α= 0,05 => регрессор q – значим.Последний шаг в анализе – это проверка гипотезы о значимости модели. Сначала опишем нужные нам формулы. 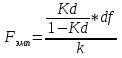 . (6) FРАСПОБР(α; k; df). (7)Гипотеза :  =0 – модель не значима:Задаем уровень значимости: α= 0,01 Находим эмпирическое значение по формуле (6):  = 9,802Находим критическое значение по формуле (7):  = 6,985Сравниваем: > => - отвергается, линейная модель значима при α= 0,01. Таким образом, анализ показал, что линейная модель значима, а также статистическую значимость параметра уравнения регрессии и показателя тесноты связи. Однако, теснота линейной связи не достаточна, чтобы признать данную модель приемлемой, а тем более хорошей. 3.3.2 Модель 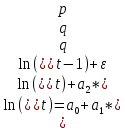В общей модели по формуле (1) параметры модели равны: 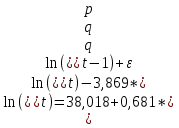= 38,018, = 0,681,  = -3,869. Следовательно, модель выглядит следующим образом:  . С помощью этой модели находим новую цену и остатки (табл. 6). Так же по первоначальным данным строим график и проводим линейный тренд. Так как коэффициент наклона в данном случае отрицательный, то и линия тренда имеет отрицательный наклон. Это наглядно видно на рис. 13. Для этого типа модели строим график  .Таблица 6 Исходные данные, новая цена и остатки, общая модель
Окончание табл. 6
|