Диплом11. Анализ взаимосвязи равновесных цен и объемов на основе заявок на оптовый рынок
 Скачать 0.5 Mb. Скачать 0.5 Mb.
|
|
Окончание табл. 8
Примечание: в скобках указаны стандартные ошибки коэффициентов. ***α=0,01, **α=0,05, *α=0,1. Оставшиеся модели подробно расписаны в приложение 10. 3.4.3 Модель Эту модель мы будем рассматривать только в зимний период и только для общего случая. По формуле (1) параметры модели равны: 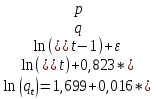 . С помощью этой модели находим новый объем и остатки (табл. 9). . С помощью этой модели находим новый объем и остатки (табл. 9).
В нашей модели коэффициент детерминации равен 70,7%, на столько процентов вариация равновесных объёмов объясняется вариацией равновесных цен. Далее осуществим проверку гипотезы о значимости регрессора, с помощью т – статистики. Путь гипотеза Задаем уровень значимости: α= 0,05 Найдем t наблюдаемое по формуле (3): Найдем t критическое по формуле (4): Сравниваем: Последний шаг в анализе – это проверка гипотезы о значимости модели. Гипотеза Задаем уровень значимости: α= 0,01 Находим эмпирическое значение по формуле (6): Находим критическое значение по формуле (7): Сравниваем: Эластичность при Найдем так же долгосрочную эластичность. В модели с долгосрочной эластичностью t → ∞, Долгосрочная эластичность равна 0,089. Таким образом, анализ показал, что обратная логарифмическая модель с Сводные данные по данной модели приведены в таблице 9. Таблица 9 Сводные данные, для общей модели
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
