Диплом11. Анализ взаимосвязи равновесных цен и объемов на основе заявок на оптовый рынок
 Скачать 0.5 Mb.
|
|
Примечание: в скобках указаны стандартные ошибки коэффициентов. ***α=0,01, **α=0,05, *α=0,1. Все расчеты подробно приведены в приложение 4. 3.4 Эконометрические модели в зимний период Зимним периодом мы будем называть период с 20 ноября по 10 марта. В зимний период конкуренция усиливается, появляется больше фирм на рынке. Из-за этого появляется большой разброс цен. 3.4.1 Модель  В 2015 году после нахождения всех точек пересечения, получилось триста тридцать четыре значения. По формуле (1) параметры модели равны:  = 266,632,  =0,017. Следовательно, модель выглядит следующим образом:  . С помощью этой модели находим новую цену и остатки (прил. 6). Так же по первоначальным данным строим график и проводим линейный тренд. Так как коэффициент наклона в данном случае положительный, то и линия тренда имеет положительный наклон. Это наглядно видно на рис. 14. Рисунок 14 Г 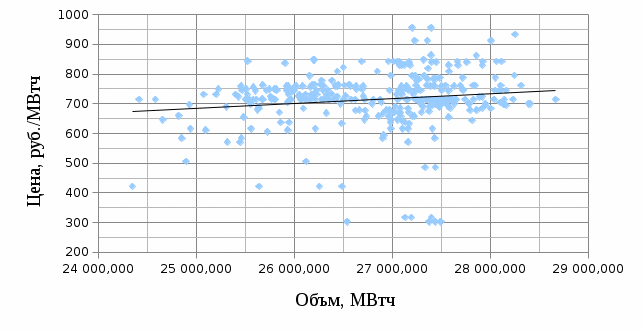 рафик равновесных точекВ данной модели коэффициент детерминации равен всего 2,2%, на столько процентов вариация равновесных объёмов объясняется вариацией равновесных цен. Далее осуществим проверку гипотезы о значимости регрессора, с помощью т – статистики. Путь гипотеза  – регрессор не значим:Задаем уровень значимости: α= 0,05 Найдем t наблюдаемое по формуле (3):  = 2,746Найдем t критическое по формуле (4):  1,967 Сравниваем: > => гипотеза – отвергается, для при α= 0,05 => регрессор q – значим.Последний шаг в анализе – это проверка гипотезы о значимости модели. Гипотеза :  =0 – модель не значима:Задаем уровень значимости: α= 0,01 Находим эмпирическое значение по формуле (6):  = 7,540Находим критическое значение по формуле (7):  = 6,712Сравниваем: > => - отвергается, линейная модель значима при α= 0,01. Таким образом, анализ показал, что линейная модель значима, а также статистическую значимость параметра уравнения регрессии и показателя тесноты связи. Однако, теснота линейной связи не достаточна, чтобы признать данную модель приемлемой, а тем более хорошей. 3.4.2 Модель  +εВ 2015 году по формуле (1) параметры модели равны: 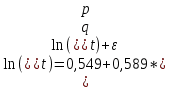= 0,549, =0,589. Следовательно, модель выглядит следующим образом:  . С помощью этой модели находим новую цену и остатки (прил. 7). Так же по первоначальным данным строим график и проводим линейный тренд. Так как коэффициент наклона в данном случае положительный, то и линия тренда имеет положительный наклон. Это наглядно видно на рис. 15. Рисунок 15 Г 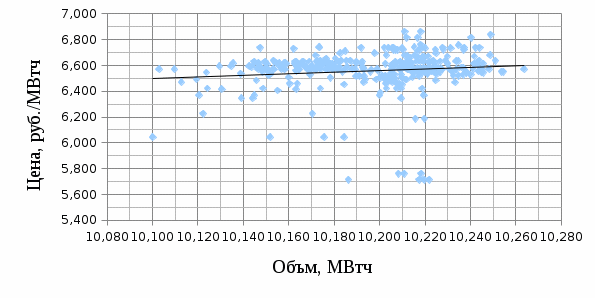 рафик равновесных точекВ нашей модели коэффициент детерминации равен всего 1,3%, на столько процентов вариация равновесных объёмов объясняется вариацией равновесных цен. Далее осуществим проверку гипотезы о значимости регрессора, с помощью т – статистики. Путь гипотеза – регрессор не значим:Задаем уровень значимости: α= 0,05 Найдем t наблюдаемое по формуле (3): = 2,113Найдем t критическое по формуле (4): 1,967Сравниваем: > => гипотеза – отвергается, для при α= 0,05 => регрессор q – значим.Последний шаг в анализе – это проверка гипотезы о значимости модели. Гипотеза : =0 – модель не значима:Задаем уровень значимости: α= 0,05 Находим эмпирическое значение по формуле (6): = 4,467Находим критическое значение по формуле (7): = 3,870Сравниваем: > => - отвергается, логарифмическая модель значима при α= 0,05. Эластичность равна 0,589, то есть изменение объема не оказывает влияние на изменение равновесных цен электроэнергии. Таким образом, анализ показал, что логарифмическая модель значима, а также статистическую значимость параметра уравнения регрессии. Однако, теснота логарифмической связи не достаточна, чтобы признать данную модель приемлемой, а тем более хорошей. Подведем итог по зимнему периоду. В таблице 8 представлены все получившиеся результаты. Таблица 8 Сводные данные за зимний период
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
