Богатин Ю.В., Швандар В.А. Экономическое управление бизнесом. Бизнесом
 Скачать 1.33 Mb. Скачать 1.33 Mb.
|
Вопросы для самопроверки и самоконтроля1. Перечислите основные затраты производства и назовите, из каких производственных ресурсов они формируются. 2. Укажите важнейшие результаты производства. 3. Для чего нужно соизмерять затраты и результаты производства при оценке эффективности предпринимательских проектов? 4. Перечислите основные условия соизмерения затрат и результатов производства. Объясните необходимость их соблюдения и экономическую сущность этого процесса. 5. Что такое дисконтирование затрат и результатов? Как осуществляется операция дисконтирования? В чем экономический смысл данной расчетной операции? 6. Укажите три основных варианта возможного дисконтирования денежных средств к определенному моменту времени. 7. Как установить величину нормы дисконтирования при проведении расчетной операции, учитывающей фактор времени? 8. Чем отличаются нормы простого и сложного процентов при дисконтировании денежных средств? Как осуществить переход от простого к сложному, и наоборот? 9. Что такое капитализация процентов и какую норму дисконтирования она отражает? 10. Смоделируйте рассуждения предпринимателя о целесообразности открытия нового дела и вложения в него определенных денежных средств. 11. Что такое абсолютная оценка доходности проекта? Укажите конкретные показатели, которые могут ее отражать, назовите основной ее недостаток. 12. Что собой представляет абсолютно-сравнительная оценка доходности проекта? В чем ее экономическая суть и чем она отличается от абсолютной оценки? 13. В чем экономический смысл сравнительной оценки доходности проекта? 14. Какая из оценок доходности проекта и когда применяется предпринимателем? В чем достоинства и недостатки каждой из них? 15. Укажите последовательность действий предпринимателя при решении вопроса об инвестировании денежных средств в наиболее рациональный проект. 16. Что понимается под затратами и результатами при оценке доходности проекта? 17. Как определяется балансовая и чистая прибыль предприятия и как можно ее просуммировать по всем временным интервалам за весь жизненный цикл проекта? 18. Как определить валовой и чистый валовой доход предприятия по отдельным временным интервалам и как рассчитать их сумму за жизненный цикл проекта? 19. Укажите типовые решения определения показателей, характеризующих абсолютную абсолютно-сравнительную и сравнительную оценки доходности проекта. 20. Объясните разницу между оценками и показателями доходности проекта. 21. Приведите конкретные примеры использования различных оценок доходности проекта и укажите последовательность их применения на практике. 22. Приведите укрупненную формулу для определения себестоимости (текущих затрат) производства продукции. 23. Сгруппируйте затраты в зависимости от их изменения под влиянием увеличения фондоемкости производства. 24. Постройте типовой график изменения себестоимости продукции от величины капитальных вложений в производство. 25. Дайте анализ изменения себестоимости производства от величины капитальных вложений в него и укажите экономическую границу поиска лучших вариантов проектных решений по минимуму затрат. 26. Сделайте сравнительный анализ эффективности двух проектных решений внутри выделенной экономической границы и укажите, как выбрать лучший из них. 27. Какой показатель для выбора одного из двух вариантов следует рассчитывать, как он называется и каков его экономический смысл? 28. Как отобрать лучший из двух альтернативных вариантов? Как поступить, если количество возможных вариантов более двух? 29. Как обосновать величину норматива сравнительной экономической эффективности дополнительных капитальных вложений? 30. Назовите основные недостатки отбора лучшего варианта из множества имеющихся альтернативных с помощью коэффициента сравнительной эффективности дополнительных капитальных вложений. 31. Трансформируйте коэффициент сравнительной экономической эффективности вложений в другой показатель для отбора лучшего варианта. Как называется такой показатель? 32. Раскройте экономический смысл показателя приведенных затрат. Для выполнения какой роли он предназначен? 33. Почему показатель приведенных затрат получил такое название? Что в нем приводится в сопоставимый вид? 34. Какими недостатками обладает критерий минимума приведенных затрат? Укажите важнейшие условия, при соблюдении которых этот критерий способен выполнять ту функцию, ради которой он создавался. 35. Можно ли воспользоваться критерием минимума приведенных затрат для выбора лучшего из вариантов вложений, если у последних имеются различия в объеме производства и качестве продукции? Объясните и обоснуйте свой ответ. 36. Каким более универсальным критерием можно воспользоваться для отбора лучшего варианта вложений? Обоснуйте этот критерий и докажите его справедливость. 37. Какой вид имеет критерий максимума приведенного эффекта? Напишите формулу этого критерия и дайте характеристику его элементов. Объясните экономическую сущность критерия и укажите, можно ли им пользоваться в условиях рыночного хозяйствования. 38. Какими недостатками обладает критерий максимума приведенного эффекта? Перечислите их и объясните, как обосновать лучшее решение, если нельзя будет воспользоваться этим критерием в силу имеющихся ограничений и условий его применения. Глава 8. Оценка эффективности инвестиций по системе международных показателей Мировая экономическая практика давно выработала универсальные методы оценки инвестиционных предпринимательских проектов, учитывающие все возможные условия их реализации. Использование таких методов позволяет оценить эффективность любого проекта достаточно точно. Для определения эффективности проектных решений разработана система показателей, с помощью которых проводится экономическая оценка любых предпринимательских проектов. Вместе с тем применения всех оценочных показателей в каждом проекте практически не требуется, поскольку все проекты существенно отличаются друг от друга. Для каждого проекта следует применить именно те показатели, которые будут учитывать их индивидуальные особенности и решать задачу по оценке их эффективности. 8.1. Показатель внутренней нормы доходности, область его применения и методика расчета Одним из наиболее важных и распространенных показателей для оценки эффективности предпринимательского проекта является показатель внутренней нормы доходности (рентабельности), наиболее полно отражающий абсолютную оценку доходности конкретного предпринимательского проекта. Его суть заключается в том, что внутренняя норма доходности характеризует величину чистой прибыли (чистого валового дохода), приходящуюся на единицу инвестиционных вложений, получаемой инвестором в каждом временном интервале жизненного цикла проекта. Пример. Допустим, предприниматель вкладывает в проект 100 ед. затрат. Через полгода он возвращает свои деньги с добавлением к ним 25 ед. дохода. Следовательно, доходность проекта составила 25% за 6 месяцев, или 50% годовых. Рассмотрим более сложный пример. Представим, что проект рассчитан на два временных интервала общей продолжительностью один год. Предприниматель вкладывает в проект 200 тыс. руб. Через полгода он получает 141,42 тыс. руб., а в конце года, завершая проект, — еще 200 тыс. руб. Тогда внутренняя норма доходности составит 41,42% за каждый временной интервал, или около 83% годовых. В приведенных примерах весь расчет инвестора осуществлялся за один и за два временных интервала. На практике жизненный цикл проекта часто включает множество временных интервалов, вследствие чего расчеты эффективности и определение внутренней нормы доходности представляют сложную систему расчетов. Проиллюстрируем это на конкретном примере (табл. 8.1), где длительность жизненного цикла проекта составляет 18 временных интервалов (один временной интервал соответствует кварталу, т.е. трем месяцам). Инвестиционная часть проекта составляет три платежа и включает два временных интервала. Эксплуатационная часть проекта начинается со второго временного интервала и продолжается до конца его жизненного цикла, т.е. 16 кварталов. Величина инвестиционных вложений, а также доходы инвестора по всем временным интервалам принимаются как величины известные. Таблица 8.1 Значения инвестиционных платежей и доходов предприятия по отдельным временным интервалам, тыс. руб.
Расчеты показателя внутренней нормы доходности по методике, речь о которой будет идти несколько ниже, дали следующие результаты: за квартал показатель составит 0,0698. В пересчете на год это величина будет соответствовать 27,95%. Много это или мало, хорошо это или плохо — определяет сам инвестор, ибо данный показатель относится к разряду абсолютных оценок доходности проекта. Если инвестор решил, что такой доход за каждый квартал жизненного цикла проекта его вполне устраивает, то он будет такой проект реализовывать (при условии, что он единственный) или включит его в список для конкурсного отбора (если есть несколько альтернативных проектов). Методически показатель внутренней нормы рассчитывается по формулам 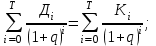 (8.1) (8.1)или 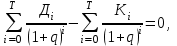 (8.2) (8.2)где Дi — доход предприятия в i-ом временном интервале: Дi = Ji (Bi ― Ci ) (8.3 ) Ji _ величина инфляционного коэффициента (формула 6.20) в i-ом временном интервале; Bi — выручка предприятия в i-м временном интервале; Ci — себестоимость продукции (без амортизационных отчислений ) в i-ом временном интервале; Ki — инвестиционные вложения в i -ом временном интервале, которые принимаются по проекту с учетом инфляции национальной валюты: Кi = Фвi · Ri , (8.4) Фвi ― коэффициент инфляции национальной валюты за период от начала инвестирования до i-го временного интервала: Фвi = (1 + Иi)(l + И2)(1 + И3) ...(1 + Ип) (8.5) И1, И2, И3 ... Ип — темпы инфляции национальной валюты в соответствующем временном интервале (в долях от единицы); Ri — инвестиционные платежи по проекту в i-ом временном интервале (без учета инфляции); q — показатель внутренней нормы доходности за временной интервал в долях от единицы; i — текущий временной интервал, принимающий значения от 0 до Т; Т — длительность жизненного цикла проекта, исчисляемая в принятых временных интервалах. Произведем расчет (а точнее, проверку ранее полученного и приведенного) показателя внутренней нормы доходности по формуле 8.1. Вначале определим суммарную величину дохода предприятия за весь жизненный цикл проекта (информацию для расчета возьмем из таблицы 8.1). 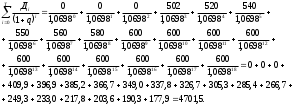 Теперь подсчитаем суммарные инвестиционные вложения. 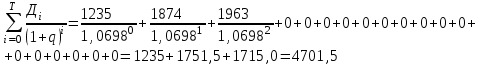 Таким образом, условие формулы 8.1 или 8.2 точно выдерживается. Суммарная величина дохода предприятия за весь жизненный цикл проекта, исчисленная с учетом фактора времени и приведенная к началу инвестирования, с высокой точностью соответствует суммарным инвестиционным вложениям (4701,5 = 4701,5). Это значит, что в данном конкретном проекте показатель внутренней нормы доходности действительно соответствует q = 0,0698. Однако возникает вопрос о том, как же определить величину искомого показателя? Ведь определить ее напрямую по формулам 8.1 или 8.2 при достаточно большом количестве временных интервалов практически невозможно. Для этого обычно пользуются при расчетах внутренней нормы доходности компьютерными программами, позволяющими в считанные доли минуты определить искомую величину с достаточной точностью. Разумеется, не всегда под рукой имеется компьютер, а к нему — не у всех есть соответствующая программа. И все же опытный расчетчик может вручную, с помощью обычного калькулятора произвести необходимые вычисления и определить показатель внутренней нормы доходности, затратив на эту процедуру около часа или несколько больше. Все зависит от того, как много временных интервалов будет использоваться в расчетах и с какой точностью надо получить решение поставленной задачи. При этом сама методика расчетных операций не очень обременительна. Она предполагает постепенное приближение получаемого результата к его окончательному виду в итерационном процессе, при котором с каждым последующим шагом все расчетные операции повторяются, производится коррекция величины показателя, и так до тех пор, пока искомый результат не будет получен. Покажем на конкретном примере, как следует применять ручной счет внутренней нормы доходности и какими приемами надо при этом пользоваться. Для простоты описания воспользуемся проектом, условия которого представлены в табл. 8.1. Итак, представим всю совокупность расчетных приемов в виде системы последовательных шагов. Первый шаг. Определим простую сумму инвестиционных вложений и сумму доходов предприятия за весь жизненный цикл проекта. Первая величина составляет, судя по исходным данным, ∑ Кi = (1235 + 1874 + + 1963) = 5074 тыс. руб. Вторая величина определяется следующим образом: ∑ Дi = 0 + 0 + 0 + 502 + 520 + ... + 600 + 600 = 9252 тыс. руб. Простое сравнение двух полученных величин свидетельствует о том, что доходная составляющая больше инвестиционной (9252 > 5074). Наличие именно такого неравенства однозначно определяет внутреннюю норму доходности как величину больше нуля. Если бы две сравниваемые величины точно совпали, то тогда искомый показатель был бы равен нулю. И наконец, в случае когда инвестиционная сумма больше доходной составляющей, искомый показатель внутренней нормы доходности представляет отрицательную величину. Но тогда инвестор, очевидно, откажется от такого проекта и примет к рассмотрению исследуемый проект лишь тогда, когда доходы предприятия будут больше инвестиций. Именно такой случай рассматривается в нашем примере. Поэтому можно перейти к дальнейшему анализу и определению величины внутренней нормы доходности. Второй шаг. Устанавливают величину искомого показателя на определенном уровне. Предположим, что расчетчик примет показатель q = 0,1, после чего произведет расчеты инвестиционных вложений и доходной составляющей проекта с применением принятой нормы доходности по формуле 8.2. Тогда у него получится отрицательная величина, ибо сумма инвестиций окажется больше доходной составляющей проекта (читатель может сам убедиться в этом, произведя соответствующие расчеты). Такой результат будет свидетельствовать о том, что установленная эмпирическим путем величина внутренней нормы доходности должна быть в данном проекте меньше 0,1 и, следовательно, дальнейший поиск связан с некоторым уменьшением величины этого показателя. Обычно если выполнять расчет чисто механически, то можно для дальнейших расчетов принять среднее значение показателя между двумя соседними расчетами, т.е. в нашем примере это будет q = 0,05, поскольку этот результат и есть средняя между 0 и 0,1. Приняв новое значение внутренней нормы доходности, переходят к новому шагу в проводимых расчетах. Третий шаг. Все расчеты точно повторяются, но уже с нормой доходности q= 0,05. Опять-таки возможны два случая: либо разность между доходной и инвестиционной частями проекта больше, либо она меньше нуля. Если имеет, место последний случай, то надо уменьшать внутреннюю норму доходности (например, до величины q = 0,025) и все расчеты повторить. Если окажется, что разность двух составляющих проекта будет положительной, т.е. больше нуля (именно так случится в нашем примере, если все расчеты произвести по аналогии с ранее выполняемыми), то значение принимаемой нормы доходности надо будет вновь увеличить, доведя ее до величины q= 0,075. Это значение будет достаточно близким к истинной величине искомой нормы доходности, которая была получена на уровне q= 0,0698 с помощью компьютерной технологии. Подобные расчеты можно продолжать многократно до получения искомого результата с такой точностью, какая будет нужна инвестору. В конечном счете потребность в информации о величине внутренней нормы доходности проекта встречается не так часто, чтобы на точности расчетов экономить несколько часов операционной работы. В заключение следует отметить, что показатель внутренней нормы доходности применяется очень широко на многих предприятиях и многими инвесторами. Но особенно важное значение этот показатель имеет для крупных производств, для масштабных проектов, при реализации которых оцениваются их стратегичность и растянутость жизненного цикла, в течение которого проект будет приносить большой доход. 8.2. Показатель чистого приведенного дохода, область его применения и методика расчета Конкретная производственно-хозяйственная и предпринимательская практика чрезвычайно разнообразны как по масштабам будущего нового дела, так и по характеру используемой технологии, планируемой организации производства, проектируемой системы управления. Кроме того, проекты могут существенно различаться по длительности жизненного цикла, по срокам инвестиционных платежей, величине и характеру поступления во времени доходов функционирующего бизнеса и т.п. Поэтому, чтобы иметь возможность отразить все имеющееся разнообразие форм и результатов предпринимательского бизнеса при оценке его эффективности, необходимо иметь несколько показателей. Одним из таких показателей является показатель чистого приведенного дохода (в экономической литературе его называют также чистой приведенной стоимостью). Показатель чистого приведенного дохода довольно широко применяется в экономике. При его исчислении нормативная величина дохода рассматривается как упущенная выгода и поэтому считается как бы дополнительно понесенными затратами. Все, что получено предпринимателем сверх общих затрат (основных и дополнительных) отражает чистый приведенный доход. Чистый приведенный доход рассчитывается по формуле 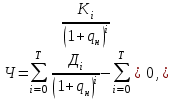 (8.6) (8.6)где Ч — чистый приведенный доход за жизненный цикл проекта; Дi _ величина дохода в i -ом временном интервале (формула 8.3); Кi _ величина инвестиционных платежей в i -ом временном интервале (формула 8.4); Т — количество временных интервалов в жизненном цикле проекта (длительность временного интервала заранее устанавливается, например месяц, два месяца, и т.д.); qн — норматив дисконтирования затрат и результатов проекта на момент начала его жизненного цикла qн = qг+ qс + qо, (8.7) где qг ― гарантированная норма получения дивидендов на вложенный капитал в высоконадежном банке (в долях единицы); qс — страховая норма, учитывающая риск вложений (в долях единицы), наличие и полноту страхования инвестиционной деятельности (если предприниматель вообще не страхует свою деятельность, то страховая норма принимается по максимуму; если страховка имеется, то страховая норма уменьшается в зависимости от полноты страхования вплоть до нуля); qо — минимальная граница доходности проекта (в долях единицы), которая по мнению предпринимателя может его устроить и принимается им для себя самостоятельно. Рассчитаем на конкретном примере чистый приведенный доход по исходным данным, представленным в табл. 8.1. Дополнительно примем норматив дисконтирования q = 0,06. Его величина складывается из следующих элементов: qг= 0,035; qc= 0,01; qо = 0,015. Тогда после подстановки исходных данных в формулу 8.6 получим 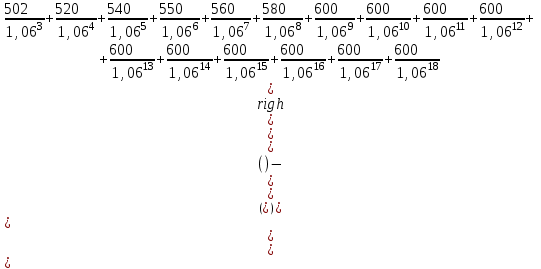 Таким образом, чистый приведенный доход составляет Ч = 381,72. Как истолковать полученный результат? Прежде всего отметим, что на величину 381,72 денежных единиц проектируемый приведенный доход предприятия за жизненный цикл проекта превысит понесенные инвестором вложения. Это значит, что будущий доход предприятия полностью возместит осуществленные инвестиции и дополнительно обеспечит ему чистый доход в указанном размере. При этом в полученную сумму дохода не включаются упущенная выгода и страховка. Не учитывается в ней и заранее установленное ограничение в минимальном доходе. Все указанные элементы дохода также будут получены предприятием, но они гарантированы включенными в расчет нормативами. Поэтому подлинный доход предприятия будет значительно выше полученной расчетной суммы. Такова природа рассматриваемого показателя, который поэтому и называется чистым приведенным доходом. В нем подлинный доход от реализации проекта не показан, но, безусловно, подразумевается при оценке эффективности инвестиций и учитывается с помощью других показателей (например, при исчислении внутренней нормы доходности). Проиллюстрируем экономический смысл показателя чистого приведенного дохода с помощью графика (рис. 8.1). Вспомним, что в рассматриваемом примере показатель внутренней нормы доходности составляет q= 0,0698. Если норматив дисконтирования при расчете будет принят на уровне внутренней нормы доходности, т.е. равным 0,0698, то чистый приведенный доход в этом случае будет равен нулю. Это значит, что сверх установленного норматива предприятие никакого дохода не получит. Теперь обратим внимание на горизонтальную линию с нулевым чистым приведенным доходом. Если норматив дисконтирования будет больше величины 0,0698, то чистый приведенный доход окажется величиной отрицательной и попадет на рассматриваемом графике в затемненную зону (например, при нормативе qн = 0,08). Иная ситуация сложится, если норматив дисконтирования будет меньше величины внутренней нормы доходности (< 0,0698), т.е., как принято в рассматриваемом примере, q= 0,06. Тогда чистый приведенный доход будет больше нуля и составит величину Ч = 381,72. Двигаясь влево к нулевой координате норматива дисконтирования, и тем самым снижая его величину, получим более высокий приведенный чистый доход, ибо движение к нулевому нормативу одновременно будет сопровождаться движением вверх по изображенной на графике кривой. При нулевой координате норматива дисконтирования чистый приведенный доход составит Ч = 4178 (разность между доходной составляющей проекта и величиной инвестиционных вложений без учета фактора времени, т.е. при qн = 0). По ранее произведенным расчетам (§ 8.1) эта разность получится, если (9252 5074) = 4178. 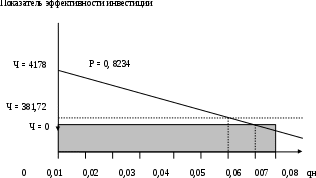 Рис.8.1. Определение чистого приведенного дохода и рентабельности инвестиций Рис.8.1. Определение чистого приведенного дохода и рентабельности инвестицийТаким образом, величина чистого приведенного дохода в огромной степени определяется не только объективными параметрами дохода предприятия и инвестициями в проект за его жизненный цикл, но и установленным нормативом дисконтирования. Если принятая норма окажется ошибочной, то будет иметь погрешность и величина чистого приведенного дохода. Поэтому при определении указанного норматива нужен тщательный анализ всей необходимой информации. Рассматриваемый показатель достаточно широко распространен на предприятиях среднего бизнеса, реже он используется на предприятиях крупного и малого бизнеса, поскольку там главное внимание уделяется другим показателям. В частности, на крупных предприятиях предпочтение отдается показателю внутренней нормы доходности, а на малых предприятиях — срока окупаемости инвестиций и срока окупаемости эксплуатируемого объекта. 8.3. Показатель рентабельности инвестиций, область его применения и методика расчета Кроме показателя чистого приведенного дохода для оценки эффективности проектного решения на предприятиях среднего бизнеса широко применяется показатель рентабельности инвестиций. Можно сказать, что оба показателя имеют одну и ту же природу и отражают одну и ту же суть, но только под разным углом зрения. Экономический смысл показателя рентабельности инвестиций заключается в том, что он отражает долю чистого приведенного дохода, приходящуюся на единицу дисконтированных к началу жизненного цикла проекта инвестиционных вложений. Этот показатель рентабельности инвестиций рассчитывается по формуле 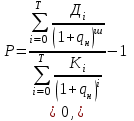 (8.8). (8.8).В этой формуле все показатели и параметры имеют тот же экономический смысл, что и в формулах 8.6 и 8.7. Если в данную формулу подставить исходную информацию рассмотренного в предыдущем параграфе примера, то при нормативе дисконтирования qн = 0,06 рентабельность инвестиций составит Р = 0,0804. Этот результат получается путем деления величины 5131,71 на величину 4749,99. Затем из частного от деления указанных величин вычитается единица и получается искомая рентабельность инвестиций — 0,0804. Что же характеризует полученный результат, каков его экономический смысл? Он означает, что, применив данный вариант, инвестор полностью вернет свои инвестиционные вложения за жизненный цикл проекта и плюс к этому получит чистый дисконтированный доход в размере примерно 8% от авансированной суммы платежей. Отмеченный результат расчета показан и на графике (рис. 8.1). Если двигаться по кривой влево и вверх до начала координат, то рентабельность инвестиций в этом случае составит Р = 0,8234. Это значит, что без учета фактора времени и упущенной выгоды, страховки и минимально установленной доходности проекта рентабельность инвестиций составит примерно 82,3%, т.е. затратив на проект 100 ден. единиц, инвестор после его окончания, получит полный доход 182,3 ден. единиц. 8.4. Показатели срока окупаемости инвестиций и нового предпринимательского дела Одним из важнейших показателей эффективности инвестиций для предприятий малого бизнеса является срок окупаемости вложений, ибо предпринимателю, не обладающему большим денежным капиталом, очень важно как можно быстрее вернуть внесенные в дело денежные средства. Поэтому очень часто при решении вопроса об инвестировании предприниматель ориентируется прежде всего на оценку срока возврата вложений. Экономическая сущность показателя срока окупаемости сводится к следующему. Предположим, предприниматель вкладывает в реализацию проекта 100 ден. единиц. В результате эксплуатации реализуемого проекта он ежегодно получает по 25 ден. единиц. Следовательно, свои авансированные денежные ресурсы предприниматель вернет через четыре года. Такая информация для него представляет большой интерес, показывает, стоит ли вкладывать деньги в данное дело и как быстро они вернутся к нему. Практика бизнеса выработала несколько показателей срока окупаемости вложений, и каждый из них имеет свое назначение и отражает какую-то сторону эффективности проекта. Срок окупаемости инвестиций. Суть расчета этого показателя может быть проиллюстрирована на графике (рис. 8.2). 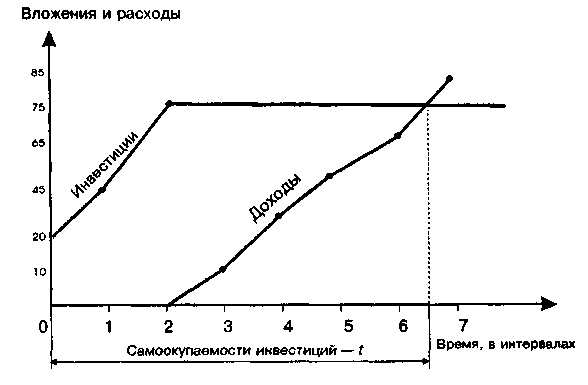 Рис.8.2. Определение срока окупаемости инвестиций По оси абсцисс откладывается текущее время в принятых временных интервалах (в годах, полугодиях, кварталах, месяца и т.п.). По оси ординат откладываются инвестиционные вложения нарастающим итогом в принятой валюте и получаемые доходы в той же валюте и также нарастающим итогом. Наступает момент, когда обе кривые пересекутся. Точка их пересечения и будет определять срок окупаемости инвестиций. На представленном рисунке этот показатель составляет величину 6,5 временных интервала. Он получается исходя из следующих принятых по условию данных: Кроме того, известно, что эксплуатация проекта начинается со второго временного интервала. Как видно из рисунка, доходная составляющая проекта пересекает на графике ее инвестиционную составляющую ровно через 6,5 временных интервалов. Это и означает, что посредством доходов в результате эксплуатации проекта предприниматель вернет свои инвестиционные вложения именно в указанный срок.
Срок окупаемости можно рассчитать по формуле 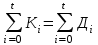 (8.9) (8.9)где Кi — инвестиционные вложения в проект в iом временном интервале; Дi — доход предпринимателя от эксплуатации проекта в i-ом временном интервале; t— количество временных интервалов функционирования проекта, за которое суммарные инвестиции сравняются с суммой доходов от эксплуатации нового дела (это и будет искомый срок окупаемости инвестиций). В рассмотренном примере суммарные вложения, как вытекает из графика, точно сравняются с суммой доходов от эксплуатации проекта через 6,5 интервала, что полностью соответствует условию формулы 8.9. Срок окупаемости действующего проекта (объекта). Срок окупаемости объекта отличается от показателя срока окупаемости инвестиций. Различие это обусловлено тем, что эксплуатация проекта начинается несколько позже, чем начинаются инвестиционные вложения. Следовательно, срок окупаемости объекта (т.е. функционирующего проекта) будет меньше срока окупаемости инвестиций. Величину показателя срока окупаемости действующего объекта можно определить по формуле tо = t ― ∆ t , (8.10) гдеtо ― срок окупаемости действующего объекта в избранных временных интервалах; t — срок окупаемости инвестиционных вложений в проект (в тех же временных интервалах); ∆t— время от начала инвестирования до начала эксплуатации проекта (в тех же временных интервалах). Если использовать условие примера, представленного на графике, то можно констатировать, что срок окупаемости действующего объекта будет согласно формуле 8.10 равен 4,5 временных интервала. Эта величина есть разность между сроком окупаемости инвестиций (6,5) и сдвигом начала эксплуатации объекта (2,0). Рассмотренный показатель характеризует тот резерв времени, которым располагает каждый предприниматель для сокращения срока окупаемости инвестиций. Ему лишь достаточно найти такие возможности, реализация которых позволит быстрее начать эксплуатацию проекта. Коэффициент нарастания дохода. Суть коэффициента нарастания дохода (рис. 8.3) сводится к следующему. 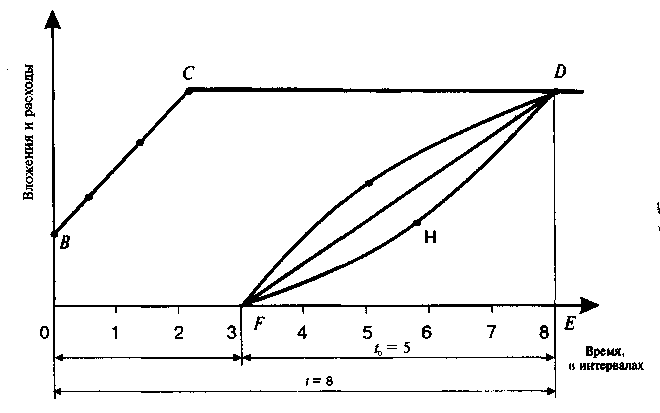 Рис.8.3. Варианты нарастания дохода при одинаковом сроке окупаемости инвестиций Предположим, что при реализации нового дела срок окупаемости инвестиций обеспечивается за 8 временных интервалов, причем доход нарастает в процессе эксплуатации проекта равномерно, т.е. в каждую временную единицу суммарный доход нарастающим итогом прирастает на одну и ту же величину. В этом случае можно констатировать, что результирующая доходная составляющая имеет линейный характер (линия FDна графике). Но такой характер нарастания дохода вовсе не обязательно будет присутствовать во всех случаях предпринимательского бизнеса. Все зависит от масштабов будущего бизнеса, принятой технологии производства, возможности ее освоения, квалификации используемых в производстве кадров, скорости реализации товаров потребителям и других факторов. Поэтому характер нарастания дохода предпринимательского проекта может и будет реально отличаться от пропорционально линейного характера. Например, он может быть таким, как показано с помощью кривой FGDили кривой FHD. Нетрудно понять, что при одном и том же сроке окупаемости инвестиций (как принято по условию в восемь временных интервалов) во всех трех зафиксированных случаях качественно и количественно характер нарастания дохода будет существенно различаться. Наилучшим вариантом для предпринимателя, безусловно, будет тот из трех рассмотренных, который позволит ему быстрее возвращать авансированные денежные средства и, следовательно, использовать их для дальнейшего развития своего бизнеса. Таким является вариант FGD, у которого с самого начала эксплуатации проекта доход будет очень быстро и прогрессивно нарастать, постепенно замедляясь к концу срока окупаемости. Самым худшим окажется вариант FHD, у которого освоение проекта вначале будет проходить в замедленном темпе и постепенно нарастать к моменту наступления срока окупаемости. Промежуточным по качеству окажется вариант FD. Естественно, различия в качестве окупаемости авансированных вложений должны быть выражены количественно, как-то оценены с помощью конкретного показателя. Это необходимо для того, чтобы иметь возможность выбирать варианты инвестирования более точно, уметь выявлять существующие резервы улучшения использования вложений, сознательно управлять процессом освоения нового предпринимательского дела. Экономический смысл предлагаемого показателя, характеризующего динамику нарастания дохода, можно рассмотреть с помощью рис. 8.4. 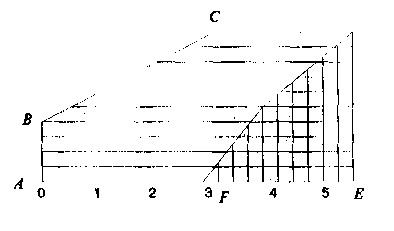 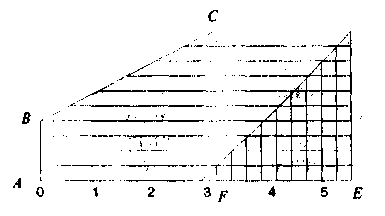 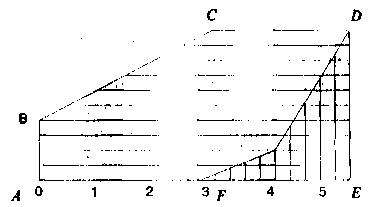 Рис.8.4. Варианты нарастания дохода Фигура ABCDEA(имеет горизонтальную штриховку) представляет собой площадь инвестирования вложений нарастающим итогом, а фигура FDEF— площадь нарастания доходов от эксплуатации нового дела (имеет вертикальную штриховку). Точка Dесть точка пересечения линий инвестирования и дохода, которая будет определять время, в течение которого наступает срок окупаемости инвестиций. Тогда в соответствии с графиком будем иметь: отрезок АЕ — длительность (срок) окупаемости инвестиций; отрезок FE — длительность (срок) окупаемости объекта; отрезок AF— период времени от начала инвестирования до начала эксплуатации проекта. Чтобы определить коэффициент нарастания дохода, необходимо взять отношение площади фигуры FDEFк площади фигуры ABCDEA. Это условие можно представить в виде формулы: 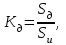 (8.11) (8.11)где Кд коэффициент нарастания дохода в процессе эксплуатации предпринимательского проекта; Sд — площадь фигуры, характеризующей нарастание дохода; Sи — площадь фигуры, характеризующей динамику инвестиций. Разумеется, эффективность инвестиций при прочих равных условиях будет тем выше, чем больше окажется коэффициент нарастания дохода, а последний окажется тем весомее, чем значительнее будет числитель Sд и чем меньшее значение примет знаменатель формулы Sи . Из рассматриваемого рисунка видно, что из трех вариантов нарастания дохода лучшим является верхний (у него самая большая площадь фигуры FDE), затем — средний вариант, а худшим — нижний вариант. При этом, как видно из рисунка, у всех вариантов срок окупаемости инвестиций абсолютно одинаков. Как же определить величину площадей исследуемых фигур? Для этого можно предложить два метода — графический и аналитический. Для использования того или иного метода необходимо иметь сведения об инвестиционных вложениях и о величине дохода в каждом временном интервале. Эта информация является необходимой и достаточной для определения коэффициента нарастания предпринимательского дохода. Располагая указанными сведениями, можно строить график, подобный тому, что показан на рис. 8.4. График лучше всего строить на миллиметровой бумаге для получения более точных результатов расчета искомого коэффициента и упрощения процедуры его определения. Для тех же целей можно применить и аналитический метод расчета коэффициента нарастания дохода, используя геометрические построения, разбивая каждую сложную фигуру на прямоугольники и треугольники. Затем определяются площади полученных фигур, а результаты суммируются. Можно решить эту задачу и с применением компьютерной программы. Выполним сравнительный расчет определения коэффициента нарастания дохода при следующих исходных данных. Пусть имеется проект инвестиционных вложений, реализация которого потребует 50 ден. единиц в течение трех временных интервалов. Проект можно осуществить с помощью различных технологических и организационных вариантов, которые обеспечат определенное разнообразие динамики доходов. Данные о величине инвестиций и доходов по временным интервалам приводятся в табл. 8.2. Показатели, представленные в табл. 8.2, рассчитаны с помощью авторской компьютерной программы «Инвест-Кредит» и отражают рассмотренное теоретическое обоснование коэффициента нарастания дохода. Как видно из таблицы, коэффициенты рассчитаны по шести вариантам. Из первых трех наилучший результат имеет первый вариант (у него налицо ускоренное получение дохода с момента начала эксплуатации проекта), худший — третий вариант. Коэффициент нарастания дохода у него самый низкий, так как начало эксплуатации проекта сопровождается низким доходом и только к середине и в конце доход возрастает. Таблица 8.2 Показатели инвестиционных вложений и динамики доходов по временным интервалам
Аналогичные результаты отмечаются у последующих трех вариантов. Самым лучшим здесь является четвертый, самым худшим — шестой вариант. Однако, как видно из таблицы, по коэффициенту нарастания дохода первые три варианта существенно хуже последующих вариантов, поскольку 4, 5 и 6 варианты начинают эксплуатироваться на один временной интервал раньше, чем первые три. Такой сдвиг во времени благотворно сказывается на рассчитываемом показателе, ибо при этом происходит уменьшение знаменателя формулы 8.11, а числитель остается без изменения. Как вытекает из формулы 8.11, более высокий коэффициент нарастания дохода имеет место при увеличении числителя Sди сокращении знаменателя Sи. Рассмотрим, отчего зависит наиболее благоприятное соотношение между числителем и знаменателем указанной формулы. Это, во-первых, более качественная подготовка проекта к эксплуатации за счет применения прогрессивной технологии, более совершенной техники, организации и управления производством. При таких условиях реализация проекта позволит быстрыми темпами освоить производственную мощность бизнеса и получать с самого начала его функционирования очень высокие доходы. Во-вторых, старание запустить проект в эксплуатацию как можно быстрее, сократив при этом время от начала инвестиционного периода до начала эксплуатации бизнеса. Это зависит от технологии предынвестиционных операций и возможности совмещения их выполнения с эксплуатацией самого проекта. В заключение необходимо отметить, что показатель коэффициента нарастания дохода лишен самостоятельного значения, а является лишь дополнительным показателем эффективности инвестиций, использование которого позволяет уточнить принимаемое решение и вскрыть существующие резервы повышения отдачи от вложений. 8.5. Экономическое обоснование отбора лучшего варианта инвестиционных вложений Очень часто в хозяйственной практике возникает проблема выбора лучшего варианта инвестирования свободных денежных средств. Обычно это происходит тогда, когда у инвестора имеются в достаточном объеме финансовые ресурсы и есть широкие возможности их использования. Как правило, задачи выбора бывают двух типов. Первый тип — выбор вариантов вложений для достижения одной и той же цели, отличающихся между собой организационными, управленческими, технологическими, экологическими или хозяйственными решениями. У таких задач цель одна, а средства для ее достижения могут быть разные, требующие различных инвестиций и обеспечивающие разные результаты при функционировании проекта. Второй тип — выбор вариантов инвестирования для достижения различных целей, у каждой из которых имеется своя потребность в инвестициях и свои возможности получения дивидендов, доходов, прибылей и пр. В методологическом плане задачи выбора обоих типов практически одинаковы с точки зрения отбора лучшего варианта вложений. По своему характеру они относятся к задачам сравнительной экономической эффективности вложений, при решении которых из множества (во всяком случае более двух) вариантов нужно отобрать для реализации только один, обладающий наилучшими показателями эффективности с позиций интересов инвестора. Рассмотрим рабочую методику отбора лучшего варианта вложений. В ее основе лежит предварительное определение привлекательности всех рассматриваемых вариантов по системе принятых для сравнения международных показателей. Такими показателями являются: • внутренняя норма доходности проекта; • чистый приведенный доход; • рентабельность инвестиций; • срок окупаемости инвестиций; • срок окупаемости действующего объекта. Каждый альтернативный вариант рассматривается на предмет возможного инвестирования, и те проекты, которые прошли предварительный отбор по каким-то соображениям инвестора, включаются в конкурс для экономической оценки их привлекательности. Затем по каждому проекту рассчитываются необходимые оценочные показатели. Результаты такого расчета сводятся в общую таблицу для обозрения и принятия после их анализа окончательного решения. Рассмотрим, как это делается. Пусть имеются четыре варианта вложений. По каждому из них определены требуемые международные показатели. Их совокупность по всем рассматриваемым вариантам представлена в табл. 8.3 (цифры условные). Представленные варианты имеют большую привлекательность для инвестора по разным показателям. Так, по показателю внутренней нормы доходности лучшим будет четвертый вариант, по чистому приведенному доходу — второй, по рентабельности инвестиций — третий, по сроку окупаемости инвестиций — первый вариант (лучшие варианты по избранным показателям в таблице выделены). Из приведенного примера вытекает одно важное условие отбора лучшего варианта: инвестор должен предварительно выделить приоритетность рассматриваемых показателей для себя, поскольку в каждом конкретном случае его выбор зависит от многих факторов (масштабы бизнеса, наличие риска вложений и функционирования бизнеса и т.п.). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
