лаб раб. 1 все. Цель работы осуществить алгоритмизацию и программную реализацию, описывающего процесс распространения компьютерного вируса в информационнотелекоммуникационной сети
 Скачать 1.04 Mb. Скачать 1.04 Mb.
|
Расчет и выбор лучшей альтернативы принципами оптимальностиДля оставшихся угроз выберем лучшие меры с помощью разных принципов оптимальности. Принцип идеальной точки Для поиска лучшей альтернативы относительно третей угрозы будем использовать принцип идеальной точки. Согласно принципу идеальной точки лучшим считается решение, расположенное в пространстве параметров ближе всего к “идеальной точке” zI: 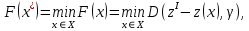 где zI – идеальная точка, D(.,.) – норма, 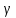 – весовой вектор. – весовой вектор.Координаты zI определяются либо интуитивно, либо как вектор максимальных значений каждого из критериев в отдельности. zI = (71, 82, 62, 58, 71) – координаты идеальной точки для третей угрозы (таблица 20). В качестве нормы будем использовать евклидову норму: 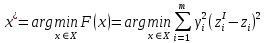 Таблица 34. Расстояния до идеальной точки
х* = 54,22 Лучшей мерой по контролю угрозы несанкционированного доступа к информации злоумышленником/конкурентом согласно принципу идеальной точки будет мера х2 – улучшение контрольно-пропускного пункта. Принцип максимина Для определения лучшей альтернативы относительно четвертой угрозы воспользуемся принципом максимина. По данному принципу каждое решение описывается наименьшей взвешенной величиной из m критериев. Затем выбирается наибольшее среди этих наименьших значений и соответствующее ему решение принимается за наилучшее: 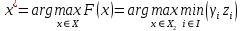 где I = {1..i} – множество номеров критериев. Иногда данный принцип называют принципом гарантированного результата или принципом наибольшей осторожности. Таблица 35. Минимальные значения критериев каждой альтернативы
x* = 6,64 Лучшей мерой по контролю угрозы преднамеренной порчи устройств согласно принципу максимина будет мера х2 – более жесткий контроль сотрудников. Принцип абсолютной уступки Для определения лучшей альтернативы относительно пятой угрозы воспользуемся принципом абсолютной уступки. Пусть сравниваются два любых решения и осуществляется переход от первого ко второму решению. Пусть при этом переходе величины одной части критериев уменьшаются, а второй — увеличиваются. Согласно рассматриваемому принципу второе решение лучше первого, если сумма взвешенных значений увеличившихся критериев больше суммы взвешенных значений уменьшившихся критериев. Это определение и принцип абсолютной уступки могут быть выражены в простой математической форме: 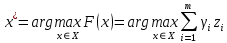 Описанный принцип позволяет улучшать качество решения за счет компенсации (уступки) уменьшения значений по одним критериям большим увеличением значений по другим критериям. Приведенная свертка в виде взвешенной суммы величин критериев может рассматриваться как целевая функция или функция качества. Таблица 36. Значения альтернатив по принципу абсолютной уступки
x* = 69,698 Лучшей мерой по контролю угрозы непреднамеренной порчи устройств согласно принципу абсолютной уступки будет мера х5 – закупка более устойчивого оборудования. Принцип относительной уступки Для определения лучшей альтернативы относительно последней угрозы воспользуемся принципом абсолютной уступки. Пусть сравниваются два любых решения и осуществляется переход от первого ко второму решению. При этом переходе относительные величины одной части критериев уменьшаются, а относительные величины второй части критериев увеличиваются. Согласно принципу относительной уступки второе решение лучше первого, если суммарное относительное увеличение взвешенных значений увеличившихся критериев больше суммарного относительного уменьшения взвешенных значений уменьшившихся критериев. Принцип относительной уступки и данное определение могут быть выражены в простой математической форме: 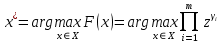 Этот принцип учитывает значения критериев, и самый простой путь улучшения решения заключается в уменьшении значений критериев с большими значениями. Таблица 36. Значения альтернатив по принципу относительной уступки
x* = 72,07 Лучшей мерой по контролю угрозы устаревания оборудования согласно принципу абсолютной уступки будет мера х1 – обновление оборудования. |
