формирование логического мышления. Дидактические игры как средство развития логического мышления у младших школьников на уроках математики
 Скачать 1.05 Mb. Скачать 1.05 Mb.
|
|
В – высокий уровень; С – средний уровень; Н – низкий уровень; «+» - положительный сдвиг; «-»- отрицательный сдвиг; 0 – прежний уровень. В соответствии с содержанием гипотезы, применим односторонний знаковый критерий. Подсчитаем значение статистики критерия Т, равное числу положительных разностей отметок, полученных младшими школьниками. Согласно таблице 16, Т=5. Из 11 пар в 6 случаях разность измерений равна нулю, следовательно, остается только 5 пар (11-6=5), то есть, n=5. Следовательно, выполняется процентное вычисление качества проделанной в формирующем эксперименте работы: 5*100/11. Качество составило 45,4%, что позволяет сделать вывод об эффективности подобранного нами комплекса дидактических игр математического содержания, направленного на развитие логического мышления младших школьников. Проанализировав степень развития мыслительных операций составляющих логического мышления, мы выяснили, что качественное изменение в результате формирующего эксперимента притерпели именно операции анализа и сравнения. Следует отметить, что количество верно выполненных заданий по методике №1увеличилось в экспериментальной группе на 17, тогда как в контрольной группе таких заданий стало больше всего лишь на 3. Учащиеся, принявшие участие в нашем эксперименте, научились видеть существенные признаки предметов, отличать их от несущественных, призводить аналитические действия с предметами, явлениями и числами. Уровень развития умения выделять существенные признаки предметов повысился у 7 учащихся: с низкого до среднего: Кан Л., Кулага А., Манди Е., Мурадов Ш., Мустафаев Ф., Халикова А.; со среднего до высокого: Коваленко А. У двух учеников: Костеневич В. и Поповой О. уровень развития аналитических способностей остался по-прежнему высоким, и еще у двух: Лесной М. и Магомедовой К. среднее развитие. Регрессивных изменений в области операции анализа у учащихся экспериментальной группы не наблюдается, тогда как в контрольной группе у 11 человек не произошло ни качественных, ни количественных изменений, а у Игнатова А. даже понизился уровень выделения существенных признаков с высокого до среднего. Методика №2 на контрольном этапе эксперимента выявила увеличение количества правильно выполненных заданий на сравнение предметов на 22,68% (119 баллов вместо 97 на констатирующем этапе эксперимента). Кроме того, произошли и качественные изменения: если на констатирующем этапе дети экспериментальной группы называли при сравнении 1-2 сходства и 1-2 различия предметов, то на контрольном этапе число называемых сходств и различий возросло до 3-4, а у некоторых детей (Манди Е., Попова О.) и до пяти. Следует отметить, что уровень развития операции сравнения остался прежним у семи учащихся, у трех произошли позитивные изменения (до среднего повысился навык сравнения у Мурадова Ш. и Мустафаева Ф. и до высокого у Манди Е.). Однако у Халиковой А. произошло снижение правильно выполненных заданий по методике №2. Результативность работы по формированию операции сравнения, таким образом, 18,1%. Для сравнения скажем, что в контрольной группе произошло ухудшение на 9%: у 11 учеников уровень развития операции сравнения не изменился, у Гаджиумарова А. снизился (на констатирующем этапе средний, на контрольном низкий). По методике №3 изменений практически не произошло: ни на констатирующем, ни на контрольном этапе в экспериментальной группе не было учащихся с низким уровнем развития операции обобщения. Методика №4 выявила 100% владения учащимися экспериментальной группы навыками классификации на этапе контрольного эксперимента: 40% на среднем уровне, 60% на высоком: у четырех учащихся наблюдается повышение навыков, у двух спад с высокого уровня на средний (хотя разница в данном случае в один правильный ответ). Таким образом, на контрольном этапе в экспериментальной группе и8 человек из 11 обладают навыками анализа, синтеза, сравнения, обобщения и классификации, развитыми на среднем и высоком уровне. У трех учащихся: Кан Л., Кулага А. и Халикова А. остался на низком уровне навык сравнения. Кулага А. не может выявлять различия предметов находит лишь одно отличие (однолинейность сравнения), Кан Л. И Халикова А. близки к среднему уровню им не хватило по одному названному сходству или различию. Тогда как в контрольной группе 7 учащихся имеют низкий уровень выявления свойств предметов, 6 учащихся не владеют операцией сравнения, двое не умеют производить обобщение и один классификацию. Выводы по главе II Логическое мышление у учащихся контрольной и экспериментальной групп на этапе констатирующего эксперимента было развито практически на одном уровне. Учеников с высоким уровнем развития - 16,7% и 27,3 % соответственно. Примерно у половины учащихся логическое мышление было развито на среднем уровне. Из четырех операций мышления, проанализированных у третьеклассников, лучше других были развиты операции обобщения (58,3% и 54,5%) и классификации (58,4% и 63,6%). Операция анализа была развита плохо, сравнение однолинейное: дети устанавливали вместо четырех 1-2 различия, либо 1-2 сходства предметов. В результате проведения формирующего эксперимента у учащихся начальных классах повысился уровень владения операциями анализа и сравнения, а значит и уровень развития логического мышления. Эксперимент показал, что в экспериментальной группе уровень сформированности приемов умственных действий (анализ, синтез, сравнение, обобщение, классификация) существенно выше, чем в контрольной группе. Это подтверждается методами статистической обработки, которые выявили, что подобранный нами комплекс дидактических игр математического содержания, направленный на развитие логического мышления младших школьников, достаточно эффективен уровень развития логического мышления у учащихся экспериментальной группы повысилось на 45,4%. В ходе эксперимента подтвердилась гипотеза: если систематически и целенаправленно использовать на уроках математики дидактические игры, то это будет способствовать развитию логического мышления младших школьников. Заключение Важнейшей задачей математического образования является вооружение учащихся общими приемами мышления, пространственного воображения, развитие способности понимать смысл поставленной задачи, умение логично рассуждать, усвоить навыки алгоритмического мышления. Каждому важно научиться анализировать, сравнивать, обобщать и классифицировать. Проведенное нами теоретическое и экспериментальное исследование показало эффективность условий развития логического мышления и обосновало справедливость предложенной системы работы, основанной на использовании дидактической игры. Анализ психолого-педагогической, методической и учебной литературы по проблеме исследования позволил нам выявить особенности развития детей младшего школьного возраста и определить данный возраст как наиболее благоприятный для формирования навыков логического мышления. Констатирующий этап эксперимента выявил недостаточный уровень развития логического мышления у учащихся начальных классов. Проверив при помощи различных методик такие операции логического мышления, как анализ, обобщение, сравнение и классификация, мы пришли к выводу о том, что большинство учащихся при выделении существенных признаков предметов и явлений испытывают затруднения, видят не все существенные признаки, могут сравнить предметы по нескольким критериям, но с подсказкой учителя. У некоторых учеников операция анализа развита на низком уровне: при выделении существенных признаков предмета или явления они смешивают существенные и несущественные признаки; при сравнении допускают множество ошибок. Операции обобщения и классификации развиты у учащихся начальных классов несколько лучше, чем анализ или сравнение, но и они зачастую осуществляются только при указании учителем оснований для данных операций. Мы подобрали комплекс дидактических игр, направленный на развитие логического мышления на уроках математики, разработали программу развития логического мышления младших школьников. Экспериментально была доказана эффективность разработанной нами программы по развитию логического мышления младших школьников и специального комплекса дидактических игр математического характера. Достоверность полученных в ходе педагогического эксперимента результатов мы обосновали с помощью статистических методов обработки данных. На контрольном этапе эксперимента учащиеся достаточно быстро и качественно анализировали предметы и явления, практически безошибочно выделяли существенные признаки предметов и на основе выделенных признаков производили верно сравнение, обобщение и классификацию. Таким образом, цель работы достигнута, гипотеза исследования подтверждена, а поставленные задачи решены. Список использованной литературы Амонашвили Ш.А. Размышления о гуманной педагогике. – М.: Академия, 2006. – 464с. Артемов А.К. и др. Основы методического мастерства учителя в обучении математике младших школьников. – Самара: СГПУ, 1999. 238 с. Артемов А.К. Развивающее обучение математике в начальных классах. – Самара: СГПУ, 1997. 120с. Безрукова В.С. Педагогика. Екатеринбург: «Деловая книга», 1999г. 340с. Веккер М.Л. Психика и реальность. Единая теория психических процессов. М: Издательство «Смысл», 1998. – 344с. Возрастная и педагогическая психология: Учеб. пособие для студентов пед. ин-тов по спец. №2121 «Педагогика и методика нач. обучения» / М. В. Матюхина, Т. С. Михальчик, Н. Ф. Прокина и др.; Под ред. М.В. Гамезо и др. – М.: Просвещение, 1984. – 256 с. Выготский Л.С. Педагогическая психология. М.,1991.144 с. Гальперин П.Я. Психология мышления и учение о поэтапном формировании умственных действий // Исследование мышления в современной психологии. – М.: Просвещение, 1966. С.236-277. Гальперин П.Я. Формирование умственных действий и понятий. – М.: МГУ, 1985. 145с. Давыдов В.В. Психическое развитие в младшем школьном возрасте / под ред. А.В. Петровского. – М.: Педагогика, 2001. – 167с. Дышинский Е.А. Игротека математического кружка (Пособие для учителя). М.: Просвещение, 1972. – 203с. 3ак А.З. Развитие умственных способностей младших школьников. М.: «Просвещение», 2004 г. 328с. Исаева Э.Г. Стандарты развития младшего школьника: Методическое пособие. Махачкала: ДИПК ПК, 2003 г. 233с. Истомина Н.Б. Методика обучения математике в начальной школе. Учебное пособие для студентов факультета начальных классов и учащихся педагогических училищ. М.: «Просвещение», 2002 г. 253с. Каптерев П.Ф. Возрастная и педагогическая психология. М., 1999. C. 210. Коваленко В.Г. Дидактические игры на уроках математики. М., 1990. С.12-13 Косма Т.В. Мышление младшего школьника. Киев,1971. 48 с. Краткий педагогический словарь / Г.А. Андреевой, Г.С. Вяликовой, И.А. Тютьковой. – М.: Дрофа, 2007. – 192 с. Кузьмина Н.В. Профессионализм деятельности преподавателя и мастера производственного обучения. М.: Высшая школа, 2009. 67с. Кулагина И.Ю. Возрастная психология: Развитие ребёнка от рождения до 17 лет: Учебное пособие третье издание. М.: УРАО, 1997. 176 с. Курбатов В.И. Как развивать свое логическое мышление. Ростов на Дону, 1997. 300с. Левитес В.В. Развитие логического и алгоритмического мышления младшего школьника // Начальная школа плюс до и после. 2006, №9. С. 15-23. Лесгафт П.Ф. Избранные педагогические сочинения: В 2 т. М., 1951. Т. 1. С. 63. Леонтьев А.Н. Деятельность. Сознание. Личность. – М.: Изд-во Политической литературы, 1975. – 121 с. Люблинская А.А. Анализ и синтез в учебной работе младшего школьника. М, 2008. 342с. Марцинковская Т.Д. Диагностика психического развития детей. – М.: ЛИНКА-ПРЕСС, 2007. – 176 с. Махмутов М.И. Современный урок. М.: «Педагогика», 2005. 184 с. Менчинская Н.А. Проблемы учения и умственного развития ученика. М.: «Просвещение», 2006. 243 с. Немов Р.С. Психология. Книга 1. / Р.С.Немов. М, 1995. 310с. Нескучная математика. 1-4 классы: занимательные материалы / авт.-сост. Н.В. Агаркова. – Волгоград: Учитель, 2008. – 125 с. Николенко Л.А. Игры в педагогическом процессе. Псков, 1997. 86 с. Овчинникова Т. Н. Личность и мышление ребенка: диагностика и коррекция / Т. Н. Овчинникова. М.: Акад. проект, 2002. 188 с. Перькова О.И., Сазанова Л.И. Интеллектуальный тренинг: учебно-методическое пособие для учителей и родителей. – СПб.: Речь, 2002. 221с. Петровский А.Г., Ярошевский М.Г. Психология: Учебник для студ. высш. пед. учеб. заведений. – 2-е изд. Стереотип. – М.: Издательский центр «Академия», 2000. – 512 с. Пиаже Ж. Речь и мышление ребенка. – М.: Педагогика – Пресс, 1999. – 528с. Психическое развитие младших школьников/Под ред. В.В.Давыдова. М.: Наука, 1990. – С. 156. Ревина Е.Г. О возможностях развития логического мышления младших школьников в условиях целенаправленного обучения/ Межвузовский сборник научно-технических статей. – Вольск, 2007. – 180с. Рогов Е. И. Общая психология: Курс лекций для первой ступени педагогического образования / Сост. Е.И.Рогов. – М.: ВЛАДОС, 2003. – 448 с. Рубинштейн С. Л. Основы общей психологии. – СПб.: Питер, 2007. 713 с. Смоленцева А.А. Сюжетно-дидактические игры с математическим содержанием: Книга для воспитателя дет. сада. М.: Просвещение, 1987. 123 с. Степанова О.А., Вайнер М.Э., Чутко Н.Я. Методика игры с коррекционно-развивающими технологиями: Учеб. пособие для студ. сред. пед. учеб. заведений / Под ред. Г.Ф. Кумариной. М.: Академия, 2003. 272 с. Столяр А.А. Педагогика математики. – Минск: Высшая школа,1986. 245 с. Стрелкова Е.А. Игра – это серьезно! // Начальная школа: плюс – минус, 2001, № 4. Сухомлинский В.А. Избранные педагогические сочинения: В 3-х т. Т.2/Сост. О. С. Богданова, В.З. Смаль. – М.: Педагогика, 1980. – 384с. Тихомиров О.К. Психология мышления. / О.К.Тихомирова. М., 1984. – 89с. Тихомирова Л.Ф. Упражнения на каждый день: Логика для младших школьников: Популярное пособие для родителей и педагогов. Ярославль: « Академия развития», «Академия Ко», 1998. – 208с. Тихомирова Л.Ф., А.В. Басов. Развитие логического мышления детей. Популярное пособие для родителей и педагогов. Ярославль: «Академия развития», 1997. 240 с. Ушинский К. Д. Избранные педагогические сочинения: В 2-х т. / К. Д. Ушинский; Под ред. А. И. Пискунова. М.: Педагогика, 1974. 586 с. Чилинрова Л., Спиридонова Б. Играя, учимся математике. М, 1993. С.6 Шилова Е.Н. Формирование мыслительного приема сравнения у детей младшего школьного возраста. Л.: ЛГПИ, 1974. – 240 с. Щедровицкий Г.П. Методические замечания к педагогическим исследованиям игры. // Психология и педагогика игры дошкольников. Под. ред. Запорожца. М.,1996. С.24 Эльконин Д.Б. Психология игры. М., 1978. С.57 Якиманская И.С. Развивающее обучение. – М.: Просвещение, 1979. 268 с. Приложение 1 Математические игры на развитие логического мышления Блок 1. Игра «Осколки». Учитель прикрепляет на доску рисунок аптечного пузырька и разнообразные "осколки". Некоторые из них совпадают по форме с пронумерованными частями. Учитель: Найдите к каждому осколку точно такую же по форме часть на пузырьке. Запишите пары одинаковых частей. Какие два осколка не имеют пары и остались лишними? 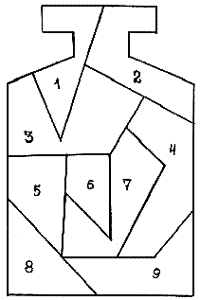 Игра «Расставь числа» Расставь числа 6, 5, 4, 3, 2, 1 в кружках так, чтобы сумма чисел в каждой прямой равнялась 12. Ответ: 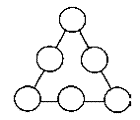 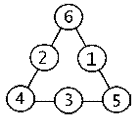 Игра в стручки Во времена царя Гороха Под смех и шутки скомороха Царь, на нос нацепив очки, Играл с царицею в стручки. Ты знаешь, как они играли? Я сообщаю все детали! Довольно простые примеры. Эти царь с царицей не очень сильны были в математике. Переложите в каждом примере один стручок - и примеры будут правильные. Примеры царя: 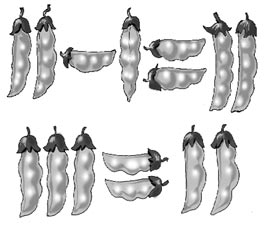 Примеры царицы:  Ответы: I + I = II; II - I = I. I + II = III; III - II = I. Игра «Найди фигурку». Цель: Учить выделять и абстрагировать свойства фигур, находить фигуры по 1, 2,3, свойствам, а также с отрицанием какого либо свойства. Материал: карточки-символы, блоки Дьенеша. Вариант 1. Учитель называет полное имя (цвет, форму и величину) задуманного блока, а дети находят его. Кто первый нашёл забирает фигурку себе. Побеждает тот, кто больше всех набрал фигур. Вариант 2. Учитель показывает знаки-символы, обозначающие форму, цвет, величину или отрицание этих свойств. Дети должны назвать и показать фигуру, отвечающую этим признакам. Ребёнок, назвавший первым, забирает фигуру себе. Побеждает тот, кто больше других набрал фигур. Игра «Шифровальщики». Цель: Отгадывать фигуру по знакам- символам с отрицанием и без отрицания, кодировать свойства фигуры, изображая знаки-символы письменно. Материал: Трафареты, цветные карандаши, бумага, карточки с изображением с донной стороны геометрической фигуры, с другой - знаков-символов, соответствующим свойствам этой фигуры. Вариант 1. Дети получают карточки, лежащие на столах вверх стороной, где изображены знаки-символы. По знакам дети отгадывают фигуру и называют её. Правильность своего ответа проверяют, перевернув карточку. Затем дети меняются карточками. Вариант 2. Учитель показывает карточку со знаками- символами, раскрывающими свойства какой либо фигуры. Дети отгадывают эту фигуру и рисуют её на листочках с помощью трафаретов. Игра «Кто быстрее?» Задание: как можно быстрее ответить на вопросы. Какая цифра, если перевернуть сверху вниз, уменьшится на 3? (Цифра 9) Какие часы показывают верное время только 2 раза в сутки? (Часы, которые остановились) Когда мы смотрим на число 3, а говорим "пятнадцать"? (Когда смотрим на часы) В известной сказке "Поди туда - не знаю куда, принеси то - не знаю что" царь послал стрелка Андрея "за тридевять земель". Внимание, вопрос! Тридевять - это сколько? (Тридевять - это 27. В Древней Руси считали девятками: тридевять - это 9 3 = 27) Сколько лет рыбачил старик из "Сказки о рыбаке и рыбке" А.С. Пушкина до того, как он поймал золотую рыбку? ("Ровно тридцать лет и три года", то есть 33 года) Сколько раз старик ходил к морю в "Сказке о рыбаке и рыбке" А.С. Пушкина, чтобы рыбка выполнила желания старухи? (Пять раз) Стоит в поле дуб. На дубе 3 ветки. На каждой ветке по 3 яблока. Сколько всего яблок? (Нисколько, так как на дубе яблоки не растут) На грядке сидят 6 воробьев, к ним прилетели еще 5. Кот подкрался и схватил одного. Сколько осталось воробьев на грядке? (Нисколько, так как остальные воробьи улетели) Блок 2. «Игра Баше». В начале игры на столе имеется несколько предметов. Необходимо взять какое-либо количество (не более заранее оговоренного) предметов за один ход. Играют два ученика. Проигрывает тот, кто возьмет последний предмет. Например, на столе 15 яблок. Разрешается брать по одному, два или три яблока. Проигрывает тот, кто возьмет последнее яблоко. Ясно, для того, чтобы не проиграть, начинающий игру должен взять первым ходом три яблока, а затем брать такое количество яблок, которое в сумме с числом яблок, взятых соперником, будет равно четырем. Игра «Поймай тройку» Цель: Развитие умение сравнивать. Материал: геометрические фигуры Учитель перемешивает фигуры и складывает их стопой. Затем снимает две верхние и кладёт их на стол. Первый ребёнок берёт из стопки фигуру, прикладывает её к паре на столе и ищет, чем похожи все три фигуры. Если он замечает какое-либо сходство, то забирает все три фигуры, если общего свойства не обнаруживается, то последнюю снятую фигурку кладут вниз стопки. Затем следующий ребёнок берёт из стопки новую фигуру и ищет общее свойство в тройке фигур. Выигрывает та команда, которая насобирает больше фигур. Игра «Найди кратное число» (для 8): 15, 18, 24, 36, 42,16, 54, 40, 48, 74, 28, 8, 12, 56, 64, 38,54, 32, 54, 81, 72. Игра «Установи правило» Задача: понять закономерность и вписать знаки + или - ” 7     000 1 400 7 = 1 200 6000 1 800 6 = 1300 000 1 400 7 = 1 200 6000 1 800 6 = 13008     000 1 500 5 = 1900 8000 1600 4 = 2400 000 1 500 5 = 1900 8000 1600 4 = 2400И   гра «Вставь пропущенные знаки». гра «Вставь пропущенные знаки».    М а К; а М; К; М М а К; а М; К; М    .а .9 К; М .а .9 К; М.д К Блок 3 Игра «Малыш и Карлсон» Малыш и Карлсон играли в игру: поочерёдно записывали цифры в ряды. Карлсон записывал любые цифры, а Малыш – по одному и тому же принципу. - Подумай, по какому принципу записывал Малыш цифры, и допиши те, которые он не дописал. Карлсон 9,4,7,19,22,31 Малыш 2,1,4,3,6,5……    30 30 И     гра « гра « Бусы» Бусы»И    з различных цифр я сделала бусы, 15 35 25 40 з различных цифр я сделала бусы, 15 35 25 40Н    о бусы были порваны. о бусы были порваны.Кто сможет их помочь собрать, 10 45 Тому поставлю пять! Игра «Магический квадрат» Расположи цифры так, чтобы сумма чисел по каждой вертикали, горизонтали и диагонали была одинакова.
|
