Инженерная химия (1-21 вопрос). Дисциплина Инженерная химия
 Скачать 0.86 Mb. Скачать 0.86 Mb.
|
|
7. Исследование кинетики гомогенных химических реакций. Реакторы периодического действия с постоянным и переменным объемом реакционной массы, реакторы идеального вытеснения. Кинетику реакции исследуют в реакторах смешения периодического действия (РИС-П). В реакторе устанавливается и поддерживается заданная температура. Далее вводится рассчитанное количество исходных реагентов и интенсивно перемешивается (начало эксперимента). В определенные промежутки времени отбираются пробы и анализируются. По найденным значениям строится концентрационная зависимость. В дальнейшем эта зависимость обрабатывается интегральным или дифференциальным методами. Интегральный метод (уравнение скорости). 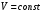 ; ; 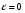 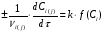 Разделим переменные: 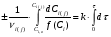 Результатом интегрирования левой части уравнения будет: 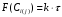 - уравнение прямой линии в координатах - уравнение прямой линии в координатах 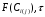 . .F(Ci(j)) После нахождения концентрационной зависимости задаются функцией 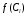 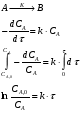 Дифференциальный метод 1 – на концентрационной зависимости выбирается произвольно несколько точек; 2 – к выбранным точкам проводят касательные и по углу наклона определяют истинную скорость; 3 – задаются уравнением скорости 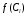 и строят график зависимости. и строят график зависимости.Расчет химического реактора достаточно сложен и трудоемок и включает в себя выбор модели реактора, технологический, конструктивно-механический расчеты. Сложность задачи расчета реакторов зависит от многих факторов: типа химической реакции, ее термодинамики, скорости теплообмена с окружающей средой, распределения вещества и тепла по объему. В ряде случаев осуществляют расчет специальных устройств, входящих в конструкцию реактора: барботеров, теплообменников, змеевиков, циклонов и других. Однако в рамках изучаемой дисциплины расчет реактора будет заключаться в выборе модели реактора и нахождении его размеров, необходимых для получения заданного количества целевого продукта. Для достижения этой цели используют расчетные уравнения, устанавливающие функциональную зависимость времени пребывания реагентов (время реакции) в реакторе () от различных факторов: = f (x, сo, r), (1) где x - заданная степень превращения; сo - начальная концентрация исходного реагента; r - скорость химической реакции. Определив время, необходимое для проведения процесса, можно рассчитать объем реактора и его основные размеры для заданной производительности. Расчетные уравнения для различных типов реакторов: - реактор идеального смешения непрерывного действия, РИС-Н: для непрерывных реакторов пользуются понятием условного времени пребывания реагентов в реакторе, которое определяется по уравнению: 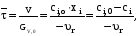 (2) (2)где, 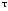 - условное время пребывания, одинаковое для всех частиц; V - объем реактора; GV,0 - объемный поток реагента, поступающего в реактор. - условное время пребывания, одинаковое для всех частиц; V - объем реактора; GV,0 - объемный поток реагента, поступающего в реактор.Зависимость объемного потока GV,0 от мольного потока Gn,0 реагентов имеет вид: G n,0 = GV,0 · с i,0 (3) - реактор идеального вытеснения, РИВ: 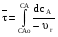 ; ; 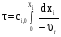 (4) (4)- реакторы идеального смешения периодического действия, РИС-П (при V=const, ε=0): 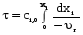 (5) (5)- РИС-П (при V≠ const, ε≠ 0): 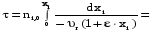 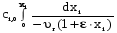 , (6) , (6)где n i,0 - начальное число молей реагента, ε- коэффициент относительного изменения объема реакционной массы, которая равна: 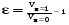 , (7) , (7)где V x=1,V x=0 – мольные объемы реакционной массы при степени превращения, равной 1 и 0. Для реакций нулевого, первого и второго порядка эти уравнения сравнительно легко решаются аналитически. Следует отметить, что уравнения для реакций второго порядка легко решаются в случае реакций с одним реагентом или с двумя реагентами при их эквимолярном соотношении на входе в реактор, то есть для реакций типа: 2 А С или А + В С (при СА,0 = СВ,0 ). В случае реакций, описываемых более сложными кинетическими уравнениями, можно пользоваться методом графического интегрирования. Для этого строят график зависимости в координатах 1/r = f (xi), вычисляют площадь, ограниченную кривой, осью абсцисс и соответствующими пределами изменения xi, отложенной по этой оси. При этом площадь под этой кривой (S) будет равняться интегралу 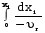 , а время химической реакции произведению: , а время химической реакции произведению: 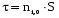 . (8) . (8)В то же время, если известно время химической реакции, объем РИС-П можно найти, используя уравнение: 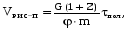 (9) (9)где G - суточная производительность; Z-запас мощности (0,1-0,15); φ-коэффициент заполнения (0,6 - 0,85); m- количество реакторов; пол - полное время периодического процесса. Это время складывается из времени химической реакции х.р и вспомогательного всп, расходуемого на загрузку реагентов, выгрузку продуктов и др.: пол = х.р + всп (10) Для определения объема реактора обычно задаются производительностью, а время пребывания рассчитывают по приведенным выше уравнениям, справедливым для данного типа реактора, после чего определяют объем реактора. Для проточных реакторов идеального смешения соединенных в каскад (К-РИС-Н) используют графический и аналитический методы расчета Графический метод расчета. Этот метод прост и позволяет рассчитать каскад реакторов идеального смешения непрерывного действия для реакции любого порядка. В основе расчета лежит уравнение (2) 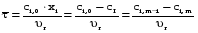 , (11) , (11)где сi, m-1 - концентрация реагента на входе в m-ый реактор; сi, m- концентрация реагента на выходе из m-го реактора. Из уравнения (11) находим, что 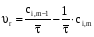 (12) (12)Как видно из уравнения (12), для m-го реактора зависимость скорости реакции от концентрации изображается в виде прямой с углом наклона, для которого 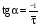 (рис. 1). С другой стороны, скорость реакции описывается уравнением (рис. 1). С другой стороны, скорость реакции описывается уравнением 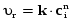 , (13) , (13)которое на графике в координатах 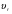 от от 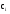 представляет собой при n>1 параболу, а при n = 1 прямую линию. Точка пересечения линии уравнений (11) и (8.12) характеризует концентрацию реагента в m-ом реакторе. представляет собой при n>1 параболу, а при n = 1 прямую линию. Точка пересечения линии уравнений (11) и (8.12) характеризует концентрацию реагента в m-ом реакторе. Для расчета К-РИС-Н графическим методом необходимо:
υr при n>1 υr=k·Cin α сi,2 сi,3 сi,1 сi Для нахождения концентрации во втором реакторе операцию повторяют, взяв за исходную точку 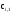 , и т. д. до тех пор, пока в последнем реакторе не будет достигнута заданная концентрация , и т. д. до тех пор, пока в последнем реакторе не будет достигнута заданная концентрация 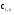 . При этом число ступеней и будет числом реакторов в каскаде, необходимым для достижения заданной степени превращения. . При этом число ступеней и будет числом реакторов в каскаде, необходимым для достижения заданной степени превращения. М Д Е Рис. 8.1. Графический метод расчета каскада реакторов идеального смешения Аналитический метод расчета. Аналитический метод расчета используется только для химических реакций первого порядка. Для этого используют уравнение: 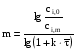 , (14) , (14)Уравнение (14) устанавливает зависимость m от отношения 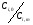 , которое выражает степень переработки реагента и величины, пропорциональной объему каждого реактора в каскаде. , которое выражает степень переработки реагента и величины, пропорциональной объему каждого реактора в каскаде.8. Особенности исследования кинетики гомогенных каталитических процессов. В гомогенном катализе исходные реагенты и катализатор находится в одной фазе, оразуя гомогенную систему. Примерами гомогенного катализа является реакции этерефикации, гидролиза сложных эфиров и др. Рассмотрим вывод уравнения скорости гомогенной каталитической реакции на примере реакции: А+В=С(кат), которая протекает по следующему механизму по стадиям: К1
К2 K3
K4
Vр=К4*С[AВkat]# В этом уравнении не извесна концентрация промежуточного комплекса [Abkat]#, для определения этой С воспользуемся принципом стационарности, согласно этому принципу: изменение концентрации любой промежуточной частицы в единицу времени, в установленном режиме равно нулю. 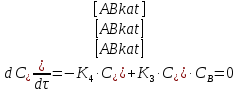 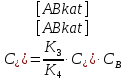 Vр=К3*С[AВkat]#*CB В последнем уравнении не известна С[AВkat]#, поэтому для ее определения воспользуемся принципом стационарности. 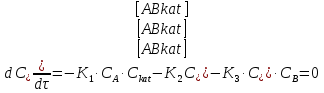 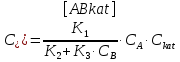 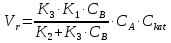 - скорость реакции для гомогенного катализа, протекающей по данному механизму. - скорость реакции для гомогенного катализа, протекающей по данному механизму.9. Кинетика гетерогенно - каталитических процессов. - наблюдаемая скорость процесса 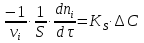 , ,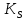 - наблюдаемая константа скорости, отнесенная к поверхности катализатора - наблюдаемая константа скорости, отнесенная к поверхности катализатора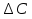 - движущая сила процесса - движущая сила процесса- Внешнедиффузионная область Скорость процесса выражается скоростью диффузионного (конвективного) переноса вещества к внешней поверхности катализатора. 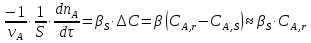 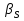 - коэффициент массопередачи реагента А из газового потока и внешней поверхности катализатора; - коэффициент массопередачи реагента А из газового потока и внешней поверхности катализатора;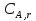 - концентрация реагента А в газовом потоке; - концентрация реагента А в газовом потоке;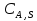 - концентрация реагента А на внешней поверхности катализатора - концентрация реагента А на внешней поверхности катализатораПроведение процесса в диффузионной области не желательно, так как в этом случае сильно затрудняются процессы теплообмена в порах катализатора. Реакция протекает в этой области, когда размеры молекул велики, а пор – малы. И когда велика толщина газо-ламинарной пленки. В этом случае для перевода процесса в другую область можно увеличить объемную скорость подачи исходного реагента. - Внутридиффузионная область. Является нежелательной областью с теми же недостатками. Протекание ГКП в этой области обусловлено в основном пористой структурой катализатора, а также геометрическими размерами и структурой молекул сырья и продуктов реакции. 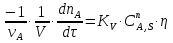 , где V – объем катализатора, , где V – объем катализатора,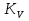 - константа скорости, отнесенная к объему катализатора, - константа скорости, отнесенная к объему катализатора,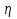 - коэффициент использования внутренней поверхности катализатора, - коэффициент использования внутренней поверхности катализатора,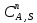 – концентрация реагенте А на внешней поверхности катализатора – концентрация реагенте А на внешней поверхности катализатораn – порядок реакции. - Стадия адсорбции Различают физическую адсорбцию и хемосорбцию. Физическая адсорбция определяется вандервальсовским взаимодействием и имеет электростатическую природу. Сильная зависимость от температуры и расстояния между молекулами. Имеет невысокую температуру адсорбции. Хемосорбция обусловлена химическим связыванием молекул, энергия очень велика и именно она играет решающую роль в гетерогенно-каталитической реакции. Сила не зависит от температуры. Для описания процесса адсорбции используют теорию Ленгмюра, согласно которой твердая поверхность однородна, молекулы образуют мономолекулярный слой и отсутствуют какие-либо межмолекулярные взаимодействия. Для практических расчетов используют уравнение изотермы Ленгмюра, устанавливая зависимость степени заполнения поверхности адсорбирующими молекулами от давления при постоянной температуры. Степень заполнения. σ σ=1 p1 p2 p, давление Адсорбция – это равновесный процесс, состоящий из двух противоположных явлений: 1 – сама адсорбция; 2 – десорбция. P2 – не минимальная зависимость >p2 – полное заполнение поверхности 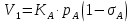 - скорость адсорбции - скорость адсорбции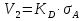 - скорость десорбции - скорость десорбцииВ состоянии равновесия V1=V2, тогда 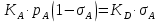 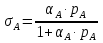 , где , где 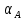 - адсорбционный коэффициент - адсорбционный коэффициент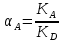 Адсорбционный коэффициент 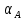 зависит от температуры и теплоты адсорбции: зависит от температуры и теплоты адсорбции: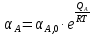 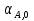 - частотный множитель, - частотный множитель, 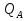 - теплота адсорбции вещества А. - теплота адсорбции вещества А.При одновременной адсорбции двух реагентов А и В: 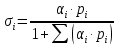 , из этого уравнения следует, что при низких давлениях , из этого уравнения следует, что при низких давлениях 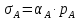 . .При высоких давлениях 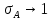 . .Для неоднородной поверхности катализатора. 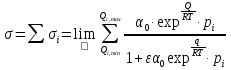 При изменении теплоты адсорбции по мере возрастания степени заполнения: Q=Q0+ΔQσ С учетом этого, уравнение изотермы адсорбции имеет вид: 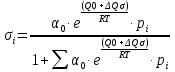 - Кинетическая область 1. Исходное вещество слабо адсорбируется 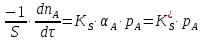 , где , где 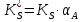 2. Исходное вещество не очень сильно адсорбируется 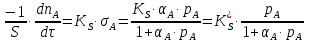 3. Исходное вещество сильно адсорбируется. 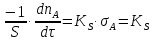 , так как , так как 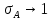 Для реакций типа А+В  продукты: продукты: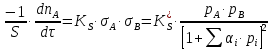 С учетом интерпретации Риделя, согласно которой реакция протекает между молекулой В из газовой среды и молекулой А, адсорбирующейся на катализаторе, кинетическое уравнение примет вид: 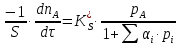 При этом 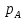 рассчитывают по уравнению Менделеева-Клаперона: рассчитывают по уравнению Менделеева-Клаперона: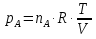 |

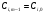 , провести прямую с тангенсом угла наклона, равным
, провести прямую с тангенсом угла наклона, равным 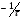 , до пересечения с кривой (прямой) в точке М.
, до пересечения с кривой (прямой) в точке М.