Инженерная химия (1-21 вопрос). Дисциплина Инженерная химия
 Скачать 0.86 Mb. Скачать 0.86 Mb.
|
|
21. Расчет реакторов, работающих в различных тепловых режимах, проектные уравнения реакторов, работающих в политропном адиабатическом и изотермическом режимах, оптимальный температурный режим и способы его осуществления в промышленных реакторах, тепловая устойчивость химических реакторов. Различают несколько видов тепловых режимов в химических реакторах: 1) Изотермический режим. Характеризуется тем, что температура исходного сырья, входящего в реактор, равна температуре в реакторе и температуре в смеси, выходящего из реактора. Это возможно, если выделение и поглощение теплоты в результате хиической реакции полностью компенсируется теплообменом с окружающей средой. Для стационарного изотермического режима при постоянстве физических свойств в системе можно записать 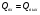 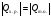 2) Адиабатический режим характеризуется отсутствием теплообмена с окружающей средой. В этом случае вся теплота химической реакции полностью расходуется на нагрев или охлаждение реакционной смеси. Для стационарного адиабатического режима: 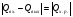 3) Промежуточный (политропный) режим характеризуется тем, что частично теплота химической реакции расходуется на изменение теплосодержания (нагрев или охлаждение) реакционной смеси, а частично на теплообмен с окружающей средой. Этот режим наиболее часто встречается в реальных химических реакторах. Промежуточный тепловой режим описывается полным уравнением теплового баланса: 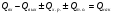 В качестве уравнения теплового баланса используют дифференциальное уравнение конвективного теплообмена: 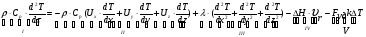 I – характеризует накопление тепла в элементарном объеме; II – характеризует конвективный перенос тепла ив направлении осей x, y, z с линейными скоростями Ux, Uy, Uz; III – характеризует перенос тепла в результате теплопроводности, где λ – коэффициент теплопроводности; IV – выделение (или поглощение) тепла в результате химической реакции; V – подвод или отвод тепла в результате теплообмена (Fуд – удельная поверхность теплообмена, K – коэффициент теплоотдачи, ΔT – движущая сила теплопередачи). 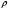 - мольная плотность; - мольная плотность; 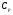 - теплоемкость; - теплоемкость; 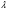 - коэффициент молекулярной теплопроводности; - коэффициент молекулярной теплопроводности; 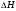 - тепловой эффект химической реакции; Vr – скорость химической реакции; Fуд – удельная поверхность теплообмена; К – коэффициент теплопередачи; - тепловой эффект химической реакции; Vr – скорость химической реакции; Fуд – удельная поверхность теплообмена; К – коэффициент теплопередачи; 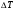 - движущая сила теплопередачи. - движущая сила теплопередачи.Проектные уравнения реакторов, работающих в политропном режиме 1) РИС-П-П Для этого реактора конвективный перенос отсутствует, т. е. части II=0 и III=0 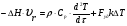 (1) (1)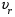 - скорость химической реакции. Для РИС-П-П: - скорость химической реакции. Для РИС-П-П: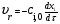 (2) (2)Подставив (2) в (1) и проведя сокращения, получаем: 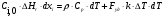 Умножим левую и правую части на объем реакционной смеси, получим окончательное выражение для теплового баланса РИС-П-П: 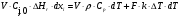 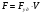 -общая поверхность тепообмена. -общая поверхность тепообмена.2) РИВ В РИВ изменение температуры происходит в одном направлении – по длине реактора. Изменение температуры за счет молекулярной теплопроводности мало и его можно не учитывать (III=0). С учетом этого общее уравнение теплового баланса для РИВ при стационарном режиме, когда накопление в реакторе тепла =0 : 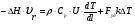 (3) (3)Скорость химического процесса в РИВ может быть выражена тем же уравнением, что и в случае РИС-П ( 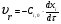 ), а линейная скорость и движение теплового потока: ), а линейная скорость и движение теплового потока: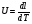 (4). (4).Подставим (4) в (3) и, сокращая, получим: 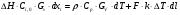 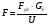 - на единицу длины реактора. - на единицу длины реактора.3) РИС-Н Для РИС-Н можно считать, что отсутствует градиент параметров, как во ремени, так и в объеме, поэтому уравнение теплового баланса составляют в целом для реактора. При стационарном режиме работы запишем уравнение теплового баланса: 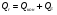 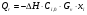 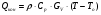 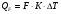 Исходя из полученных общих уравнений, Отражающих политропный режим можно найти проектные уравнения для адиабатического и изотермического режимов. Проектные уравнения реакторов, работающих в адиабатическом режиме Реактор, работающий в адиабатическом режиме представляет собой аппарат, стенки которого изолированы от окружающей среды. Т. к. при адиабатическом режиме отвод тепла отсутствует, то V=0 1) РИС-П 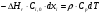 (5) (5)T T0 x α Если принять, что значения ΔHr, Cp – постоянные, то после интегрирования уравнения (5): 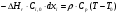 или 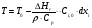 (6) (6)T – температура на выходе, T0 – температура на входе в реактор. 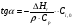 . .При проведении реакции до конца, т. е. xi=1 из уравнения (6) получим уравнение: 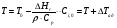 T – температура реакционной массы в адиабатическом процессе; 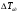 - адиабатическое изменение температуры. - адиабатическое изменение температуры.2) В проточных реакторах вытеснения и смещения также отсутствует теплообмен, поэтому для проточного вытеснения РИВ получаем: 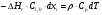 (7) (7)Если принять, что 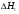 и и 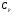 не зависят от температуры, то из (7) следует: не зависят от температуры, то из (7) следует: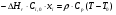 3) Для проточного реактора смешения РИС-Н: 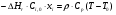 Таким образом, для всех реакторов при адиабатическом режиме и постоянных значениях 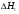 и и 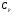 тепловой баланс выражается в виде одинаковых уравнений. тепловой баланс выражается в виде одинаковых уравнений.Проектные уравнения реакторов, работающих в изотермическом режиме Химические процессы при постоянных температурах можно провести в непрерывно действующих реакторах, т. е. для РИС-П такой режим невозможен, а возможен только для РИС или РИС-Н. Для них можно принять, что 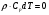 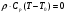 1) С учетом этих замечаний получим для РИВ обобщенное уравнение: 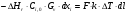 2) Для проточного реактора смешения РИС-Н можно записать, что 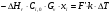 Оптимальный температурный режим и способы его осуществления в промышленных реакторах Температурный режим проведения химического процесса, обеспечивающий экономически целесообразную максимальную производительность едины объема реактора по целевому продукту называется оптимальным. Подход к разработке оптимального температурного режима может быть различным, в зависимости от типа химической реакции. Рассмотрим влияние кинетического уравнения на выбор температурного режима: 1) Простые необратимые реакции Уравнение скорости экзо- и эндотермических реакций можно записать: 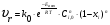 (8) (8)Как видно из уравнения скорость химической реакции является функцией нескольких переменных: температуры, степени превращения реагентов.. Очевидно, что максимальная интенсивность реактора будет обеспеченна при проведении процесса с наибольшей скоростью. С повышением температуры, В соответствии с уравнением Аррениуса, k монотонно возрастает. Из уравнения (8) видно, что принципиальных ограничений повышения темпера туры, с целью повышения скорости, необратимых реакций нет. С ростом степени превращения реагента скорость реакции падает, для компенсации этого уменьшения целесообразно повысить температуру. Эндотермическая реакция сопровождается поглощением энергии теплоты ⇒такие реакции невыгодно проводить в адиабатических условиях, т. к. по мере протекания реакции ее скорость будет уменьшаться за счет снижения температуры и за счет увеличения степени превращения. Более разумно проводить эндотермические процессы с промежуточными или разовым подводом тепла. В случае экзотермических реакций рост степени превращения сопровождается выделением теплоты ⇒ в адиабатическом режиме это приводит к росту температуры реакционной смеси. Уменьшение скорости химической реакции частично компенсируется увеличением константы скорости реакции. Проводя такую реакцию в адиабатическом режиме можно обеспечить высокую скорость химической реакции и высокую производительность реактора в автотермическом режиме без использования посторонних источников теплоты. При этом теплота реакционной смеси, выходя из реактора, служит для нагрева исходных реагентов на входе в реактор: 2) Обратимые химические реакции В случае обратимых экзотермических реакций увеличение температуры будет приводить к возрастанию скорости реакции, однако в соответствии с принципом Ле-Шателье равновесие будет смещаться в сторону исходных реагентов, следовательно такие реакции следует проводить в оптимальных условиях. Проанализируем условие обеспечения оптимального температурного режима на примере реакции i-ого порядка: A↔B Скорость: 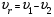 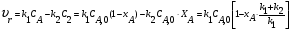 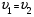 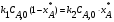 , откуда , откуда 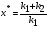 (9) (9)С учетом уравнения (9) получаем: T 1 2 3 ЛОТ 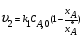 (10) (10)Из уравнения (10) видно, что скорость обратимой реакции зависит не только от константы скорости k, но и от равновесной степени превращения x*. С ростом температуры константа скорости k возрастает, а x* уменьшается. Таким образом, наблюдается противоположные влияния температуры на скорость реакции, и ⇒определить оптимальную температуру реакции для обратимой экзотермической реакции. И процесс будет вблизи линии оптимальных температур (ЛОТ). Тепловая устойчивость химических реакторов Под устойчивым тепловым режимом реактора подразумевается режим, при котором система может самопроизвольно вернуться в исходное состояние при наличии каких-то возмущений (изменение температуры, реагентов, среды и т. д.). Рассмотрим устойчивый термодинамический режим реактора на примере реакции: A→B + Q Реакция экзотермическая, первого порядка, без катализатора, необратимая, без изменения молей. Рассмотрим этот режим для адиабатического реактора. Для него можно записать следующее уравнение теплового баланса: 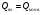 , ,где Qr количество энергии, выделившегося в ходе реакции (приход тепла); Qконв. - конвективный унос тепла с продуктами реакции (расход тепла). 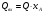 , , 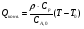 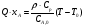 (11) (11)Обе части уравнения характеризуют изменение тепла в адиабатическом реакторе в зависимости от степени превращения. При этом устойчивый тепловой режим будет соответствовать равенству прихода и расхода тепла. На основании уравнения (11) построим графические зависимости прихода и расхода тепла в зависимости от температуры. 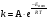 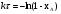 Для прихода Для расхода XA=1 Qr T0 T α Qкон T0 T tgα=  Совместив эти графические зависимости на одном рисунке, при этом точки пересечения этих линий будут соответствовать приходу и расходу тепла, а значит, будут соответствовать устойчивой работе реактора. TN N Q T0 T M N L Q T0 T Qрасх Qпр L Q T0 T T1 1) 2) 3) 1) В этом случае реактор работает в устойчивом тепловом режиме. Например, если T0 возрастает, то изменяется соотношение между расходом и приходом тепла, т. к. расход тепла больше прихода, то будет происходить охлаждение реакционной массы и система самопроизвольно вернется в точку L. Однако, случаю этому случаю соответствует низкая степень превращения XA и, следовательно, реактор будет работать в неоптимальном режиме; 2) Соответствует неустойчивому и неоптимальному режиму; 3) Соответствует устойчивому и оптимальному режиму. Для перевода системы из неоптимального в оптимальный режим используют следующие приемы: 1) повышение T0: 2) изменить α (повышение 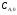 ): ):L T0 N Q T L T0 N Q T0 T 3) изменение времени пребывания в реакторе: N L XA T Q T0 |
