Инженерная химия (1-21 вопрос). Дисциплина Инженерная химия
 Скачать 0.86 Mb. Скачать 0.86 Mb.
|
|
Расчет высоты колонны. Учитывая, что 1 моль вещества А, прореаг. в жидкости заменяется на 1 моль свежего вещества из газовой фазы и комбинируя уравнение мат баланса и уравнения скорости получаем: 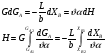 Т.к концентрация вещества А в газе примерно одинакова во всех точках объема, то уравнение имеет вид: 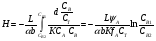 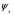 - константа Генри. - константа Генри. Ст - концентрация всех веществ в жидкой фазе. Аппараты типа смеситель-сепаратор Применяются для систем ж-ж(н) и очень редко для систем г-ж. Обычно в реакторные узлы такого типа входят 2 устройства: - смеситель, т.е реактор, в котором осуществляется химическое превращение. - сепаратор, в котором происходит разделение продуктов. Аж+Вж=Сж+Дж Аж Вж Сж Дж Сепаратор Смеситель Эффективность разделения С и Д будет зависеть от разности плотностей этих веществ. Смеситель предполагает наличие эффективного перемешивающего устройства. 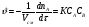 Если реакция протекает в смесителе, то при условии высокой гомогенности системы расчет можно вести аналогично РИС-Н. Если происходит последовательное взаимодействие реагентов, то расчет ведут аналогично РИС-Н-К. Модели смешения фаз в реакторе полупериодического действия. Аг+Вж=продукты В таких реакторах газ непрерывно подается в жидкость в течение времени, за которое жидкий реагент В полностью вступает в реакцию. При этом концентрация вещества А в газовом потоке не изменяетсяв ходе процесса. Вещество В медленно реагирует с веществом А и его концентрация постепенно снижается. Вж Аг Если при этом протекает реакция второго порядка, представленная уравнением: 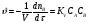 После преобразования получим: 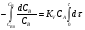 Откуда: 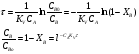 19. Основы расчета реакторов для проведения топохимических процессов, реакторы с псевдоожиженным слоем при наличии уноса и возврата твердых частиц, расчет основных геометрических размеров реакторов для проведения топохимических процессов. При проектировании реакторов, в которых осуществляются топохимические процессы между газообразной (жидкой) и твердой фазами необходимо учитывать следующие факторы:
В реакторах с кипящем слоем, а также с движущейся твердой фазой, возможно изменение частиц твердой фазы во время протекания реакции, из-за механических повреждений.
Для упрощения расчетов используют различные методы: - большой избыток газовой (жидкой) фазы, при этом ее степень превращения будет практически ничтожно мала, что приведет к постоянству концентрации этой фазы; - считают, что реакторы с движущейся твердой фазой и с кипящим слоем близки к идеальным моделям; - принимают размеры частиц постоянными и неизменяющимися в ходе химических превращений; - изотермический режим реактора. Расчет реакторов сводится к определению геометрических размеров реактора (диаметр и высота). Для расчета используют критериальное уравнение, отвечающее режиму идеального смешения (кипящий слой) из которых находят рабочую скорость. Для осуществления топохимических процессов используют реактора такой же конструкции как и для гетерогенно-каталитических процессов: - с неподвижной твердой фазой; - реактора с кипящим слоем твердой фазы; - реактора с движущейся твердой фазой (прямоток, противоток). Наибольшее распространение получили реактора с кипящим слоем и движущейся твердой фазой. 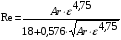 где 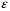 - порозность кипящего слоя (0,35 – 0,6); - порозность кипящего слоя (0,35 – 0,6);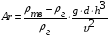 Далее определяют рабочую скорость из уравнения: 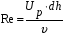 , где , где 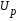 - рабочая скорость; - рабочая скорость;После определения рабочей скорости газа, рассчитывают диаметр реактора: 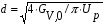 Высоту псевдоожиженного слоя рассчитывают по массе твердого реагента: 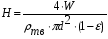 , где W – масса твердой фазы; , где W – масса твердой фазы;Для реакторов с прямоточным движением исходных реагентов в режиме вытеснения рабочая скорость равна: 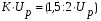 Высота реактора равна: 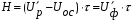 Для реактора с противоточным движением исходных реагентов расчетные уравнения будут следующими: 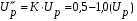 Высота рассчитывается по уравнению: 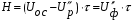 Наиболее трудной задачей при расчете геометрических размеров реактора является нахождение времени реакции. Технологический расчет времени контакта по средней степени превращения твердого реагента. При известном среднем радиусе твердой частицы и известной кинетики топохимического процесса расчет реактора сводится к определению средней степени превращения твердой фазы и уточнения времени контакта исходных веществ для последующего определения геометрических размеров реактора. Смесь частиц с различными, но постоянными размерами в режиме идеального вытеснения. Уравнение материального баланса для данной смеси можно записать: 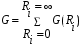 Каждая частица с размером 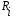 при заданном времени пребывания твердого реагента в реакторе будет иметь строго определенную степень превращения при заданном времени пребывания твердого реагента в реакторе будет иметь строго определенную степень превращения 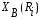 . .Следовательно, среднюю степень превращения твердой фазы можно рассчитать по уравнению: 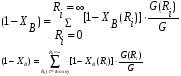 Как известно, частицы меньших размеров взаимодействуют с газом быстрее, чем крупные частицы. Однако поскольку время пребывания частиц в реакторе одинаково, некоторые частицы с размерами 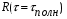 успевают полностью прореагировать за меньшее время. успевают полностью прореагировать за меньшее время.Тогда для таких частиц рассчитанная степень превращения составит величину больше 1, что не имеет физического смысла. После определения средней степени превращения определяют время контакта с газовой фазой исходя из области протекания топохимического процесса. 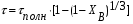 - кинетическая область; - кинетическая область;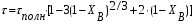 - внутридиффузионная область; - внутридиффузионная область; - внешнедиффузионная область. - внешнедиффузионная область.Твердый реагент состоит из частиц равных и неизменяющихся размеров и находящихся в режиме идеального смешения. Для расчета реактора используют дифференциальную функцию распределения времени пребывания 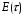 твердой фазы в кипящем слое. твердой фазы в кипящем слое.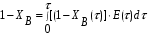 Для потока твердых частиц в режиме идеального смешения со средним временем пребывания: 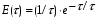 Для частиц одинакового размера полностью превращающихся за время 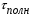 уравнение будет следующим: уравнение будет следующим: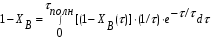 В зависимости от области протекания процесса конечное уравнение для расчета средней степени превращения твердой фазы будет иметь вид: - внешнедиффузионная область: 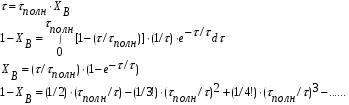 - кинетическая область Если лимитирующей стадией является химическая реакция 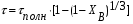 то подставляя уравнение: 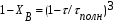 получим 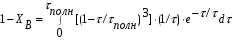 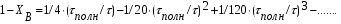 - внутридиффузионная область Если лимитирующей стадией является диффузия газа через слой золы 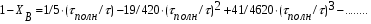 Исходное вещество представляет собой смесь частиц с различными, но постоянными размерами и находящимися в режиме идеального смешения Так как размеры частиц в ходе реакции не изменяются, то можно предположить, что распределение по размерам в исходном потоке, в кипящем слое и выходном потоке одинаковы, таким образом: 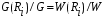 где G – относится к входящему и выходящему потоку твердой фазы; W – масса твердой фазы, находящейся в кипящем слое. Время пребывания частиц с размером Ri равно времени пребывания твердого вещества в псевдоожиженном слое 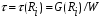 Обозначая через 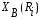 - степень превращения твердой фазы с размерами Ri в псевдоожиженном слое можно записать: - степень превращения твердой фазы с размерами Ri в псевдоожиженном слое можно записать: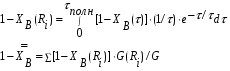 Комбинируя эти уравнения с учетом области протекания можно получить: - для внешнедиффузионной области: 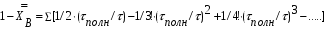 - для кинетической области: 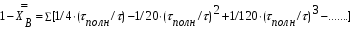 - для внутридиффузионной области: 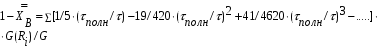 20. Основы расчета реакторов с неидеальным потоком движения реакционной среды, использование ячеечной и диффузионной модели для расчета реальных реакторов. В идеальных проточных реакторах частицы находятся в одно и то же время 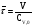 . При одинаковом времени пребывания достигается и одинаковая степень превращения Xi. . При одинаковом времени пребывания достигается и одинаковая степень превращения Xi.Отклонение от идеального течения. В реальных проточных реакторах время пребывания может отличаться от 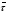 , что приводит к изменению Xi, а изменение Xi будет приводить к изменению материального баланса реактора. На течение жидкости в реакторах оказывает влияние следующие группы факторов: , что приводит к изменению Xi, а изменение Xi будет приводить к изменению материального баланса реактора. На течение жидкости в реакторах оказывает влияние следующие группы факторов:- конструкционный фактор; - диффузионный фактор; Использование ячеечной и диффузионной модели для расчета реальных реакторов Ячеечная модель Реальный аппарат мысленно расчленяют на N последовательных соединенных ячеек идеального смещения. Как правило при N<10 удовлетворительно описывается реальный реактор. Число ячеек N, заменяющих реальный реактор, является единственным параметром ячеечной модели. При известном N расчет реактора на основе ячеечной модели по сути дела не отличается от расчета РИС-Н-К и представляет собой последовательное решение уравнений математической модели каждой ячейки идеального смешения. Число ячеек в ячеечной модели устанавливают экспериментальным путем. Диффузионная модель В диффузионной модели существует некий промежуточный гидродинамический режим между идеальным вытеснением и смешением. Диффузионная модель проточного реактора учитывает перемешивание реакционной среды в осевом направлении, вызванными различными видами диффузии. Общее уравнение потока веществ для однопараметрических моделей химических реакторов можно записать с помощью уравнения: 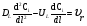 Или 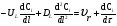 (1), (1),где UL – линейная скорость потока в направлении оси реактора; DL – коэффициент продольной диффузии. Первый член уравнения (1) ответственный за осевое перемещение, интенсивность которого определяется коэффициентом DL. Второй член уравнения характеризует конвективный перенос i-ого вещества со скоростью UL. В предельных случаях уравнение может быть использовано для описания РИВ и РИС-Н. Если первый член = 0, 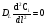 , то , то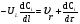 и получаем РИВ. и получаем РИВ.Если 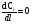 , т. е. имеет место равномерное распределение по объему, то , т. е. имеет место равномерное распределение по объему, то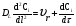 Следует отметить, что расчет РИС-Н по уравнению затруднен, т. к. в РИС Ci(l) является разрывной функцией (на входе в реактор происходит скачкообразные изменения от Ci,0 до входной концентрации Ci). Степень приближения реальной гидродинамической обстановки к одной из реальных зависит от соотношения величин конвективной и диффузионных составляющих уравнения динамики. Используя методы теории подобия, являющихся мерой относительной эффективности –х физических процессов: конвективного переноса в направлении оси реактора и диффузионного перемешивания: 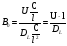 B0 – критерий Боденштейна или диффузионный критерий Пекле. Если B0 – большое значение, то конвективный перенос >> диффузионного перемешивания, а это возможно при больших значениях длины и линейной скорости, либо при низких значениях DL. Если B0=∞ - получаем РИВ. Если B0 – малое значение, что возможно при малых l или U, либо при больших DL, то преобладает диффузионное перемешивание. Если B0=0 - получаем РИС-Н. Значение критерия Боденштейна коррелирует с типом диффузионной модели м находится также экспериментальным путем. Расчеты на основе диффузионной модели существенно сложнее, чем на основе ячеечной. Аналитическое решение уравнения диффузионной модели возможно лишь для стационарного реактора при проведении в нем реакции 1-ого порядка, скорость которой является линейной функцией от концентрации: 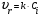 Экспериментальное определение параметров ячеечной и диффузионной модели Интегральная функция распределения I(τ). τ0 τ I(τ) S0 I(τ) – объемная доля потока, находящегося в реакторе в течении времени меньше τ. Свойства интегральной функции распределения: 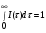 , , 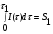 -объемная доля потока, находящегося в реакторе в течении времени меньше τ1. -объемная доля потока, находящегося в реакторе в течении времени меньше τ1. 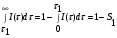 - объемная доля потока, находящегося в реакторе в течении времени больше τ1. I(0)=0 - объемная доля потока, находящегося в реакторе в течении времени больше τ1. I(0)=0Дифференциальная функция распределения E(τ). 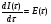 E(τ)τ2 τ E(τ) S’ S2 – плотность распределения времени проживания частиц в реакторе. Свойства дифференциальной функции распределения: 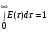 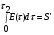 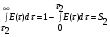 Получение информации о функциях распределения времени пребывания: Для получения информации о функции распределения используют метод трассеров или индикаторов. Суть метода: подача на вход реактора специальных веществ, которые можно легко определить на выходе из реактора; при этом трассер должен изменить гидродинамический режим в реакторе. В качестве трассеров можно использовать красители, фосфорицирующие вещества, кислоты и щелочи, радиоактивные изотопы и др. Для получения требуемой функции распределения используют различные способы ввода трассера. Функция распределения времени пребывания идеальных проточных реакторов. РИС-Н τ I(τ) τ E(τ) 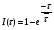 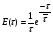 РИВ 1 τ I(τ) Интегральная функция распределения I(τ) разрывная функция, имеющая 2-а значения: 0 и 1. При τ < 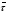 , I(τ)=0 , I(τ)=0При τ > 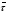 , I(τ)=1 , I(τ)=1Дифференциальная функция распределения - особая функция, т. к. является 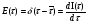 функция Дирака функция Дирака∞ τ E(τ) При τ = 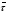 , , 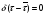 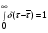 Функция приближающая по свойствам к δ-функции: τ I(τ) τ = 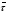 , E(τ)=∞ , E(τ)=∞< 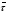 , E(τ)=∞ , E(τ)=∞> 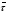 , E(τ)=0 , E(τ)=0Функция распределения для реальных реакторах Ячеечная модель Интегральная функция распределения I(τ) для ячеечной модели имеет следующий вид: 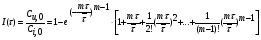 m – число ячеек Интегральная функция распределения времени пребывания для ячеечной модели при различных значениях N. N=1 N=20 τ 1 0,5 I(τ) 1 N=5 1 5 20 ∞ Дифференциальная функция распределения E(τ) для ячеечной модели имеет вид: 2 τ 1 0,5 E(τ) 1 1 4 3 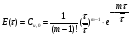 1) N=1 2) N=2 3) N=6 4) N=∞ Диффузионная модель Дифференциальная функция распределения времени пребывания для диффузионной модели при различных значений параметра 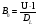 3 τ 1 0,5 E(τ) 1 5 4 2 1 1) B0=0,1; 2) B0=1; 3) B0=10; 4) B0=17,8; 5) B0 →∞ |
