Разбор вариантов ЕГЭ. Разбор типовых вариантов заданий ЕГЭ по математике_20181010_2236. Двух частей, которые различаются по содержанию, сложности и числу заданий 8 заданий первой части (задания 18) с кратким ответом в виде целого числа или конечной

• Название: Двух частей, которые различаются по содержанию, сложности и числу заданий 8 заданий первой части (задания 18) с кратким ответом в виде целого числа или конечной
• Анкор: Разбор вариантов ЕГЭ
• Дата: 15.03.2022
• Размер: 0.61 Mb.
• Имя файла: Разбор типовых вариантов заданий ЕГЭ по математике_20181010_2236.docx
• Тип: Документы; #398425
• страница: 13 из 16

Неравенства

В задании №15 профильного уровня ЕГЭ по математике необходимо решить неравенство. Чаще всего неравенство связано с логарифмами или степенными выражениями. Для успешного выполнения необходимо хорошо оперировать данными выражениями.

Разбор типовых вариантов заданий №15 ЕГЭ по математике профильного уровня

Первый вариант задания (демонстрационный вариант 2018)

Решите неравенство: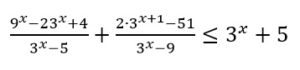

Алгоритм решения:

1. 
   Вводим подстановку.
   
2. 
   Записываем выражение неравенства в ином виде.
   
3. 
   Решаем неравенство.
   
4. 
   Возвращаемся к подстановке.
   
5. 
   Записываем ответ.
   

Решение:

1. Вводим замену  t = 3^x . Тогда исходное неравенство примет вид: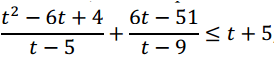



2. Преобразуем его: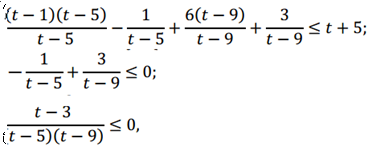



3. Отсюда получаем решение t ≤ 3; 5 < t < 9.

4. Возвратимся к переменной х.

При t ≤ 3 получим: 3^x ≤ 3 , следовательно x ≤ 1

При 5 < t < 9 получим: 5 < 3x < 9, следовательно log₃5 < x < 2.

5. Решение исходного неравенства:  x ≤ 1 и log₃5 < x < 2.

Ответ: (-∞;1] (log₃5;2)

Второй вариант задания (из Ященко, №1)

Решите неравенство   .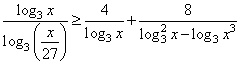

Алгоритм решения задания:

1. 
   Вводим замену.
   
2. 
   Записываем неравенство в новом виде.
   
3. 
   Решаем неравенство.
   
4. 
   Возвращаемся к переменной х.
   
5. 
   Записываем ответ.
   

Решение:

1. Вводим замену t = 3^x.

2. Тогда неравенство примет вид:

3. Решаем его: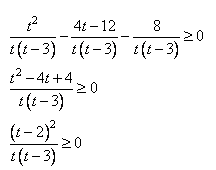



Отсюда t < 0; t = 2; t> 3.

4. Возвращаемся к переменной х.

При t < 0 получаем:

 ,

откуда 0 < x < 1.

При t = 2 получаем:

 ,

откуда x = 9.

При t > 3 получаем:

 ,

откуда x > 27.

5. Решения исходного неравенства:

 .

Ответ:  .

Третий вариант (Ященко, № 5)

Решите неравенство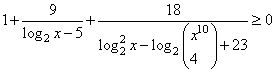 

Алгоритм решения:

1. 
   Находим ОДЗ выражения в неравенстве.
   
2. 
   Преобразуем неравенство к иному виду.
   
3. 
   Вводим замену и решаем новое неравенство.
   
4. 
   Возвращаемся к переменной х.
   
5. 
   Записываем ответ.
   

Решение:

1. Запишем ОДЗ:   .

log₂х-5≠0, log₂х≠5, х≠32

2. Преобразуем неравенство: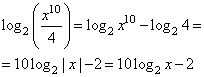



или



Получаем новое неравенство:

.

Вводим замену   , тогда неравенство принимает новый вид. И его легко решить: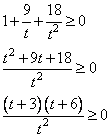



Размещаем полученные решения на числовую ось: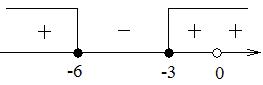



Возвращаемся к переменной х. Рассмотрим два случая: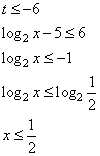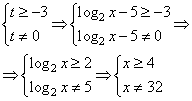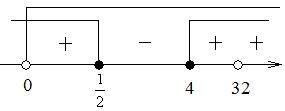





Ответ: