Разбор вариантов ЕГЭ. Разбор типовых вариантов заданий ЕГЭ по математике_20181010_2236. Двух частей, которые различаются по содержанию, сложности и числу заданий 8 заданий первой части (задания 18) с кратким ответом в виде целого числа или конечной

Название	Двух частей, которые различаются по содержанию, сложности и числу заданий 8 заданий первой части (задания 18) с кратким ответом в виде целого числа или конечной
Анкор	Разбор вариантов ЕГЭ
Дата	15.03.2022
Размер	0.61 Mb.
Формат файла
Имя файла	Разбор типовых вариантов заданий ЕГЭ по математике_20181010_2236.docx
Тип	Документы #398425
страница	11 из 16

1 ... 8 9 10 11 12 13 14 15 16

Значения функции: наибольшее и наименьшее

В задании №12 ЕГЭ по математике профильного уровня нам необходимо найти наибольшее или наименьшее значение функции. Для этого необходимо воспользоваться, очевидно, производной. Посмотрим на типовом примере.

Разбор типовых вариантов заданий №12 ЕГЭ по математике профильного уровня

Первый вариант задания (демонстрационный вариант 2018)

Найти точку максимума функции y = ln(x+4)²+2x+7.

Алгоритм решения:

Определяем область определения функции.
Находим производную.
Определяем, в каких точках производная равна 0.
Исключаем точки, не принадлежащие области определения.
Среди оставшихся точек ищем значения х, в которых функция имеет максимум.
Записываем ответ.

Решение:

1. Ищем значения х, при которых логарифм имеет смысл. Для этого решаем неравенство:

(x+4)² > 0

Поскольку квадрат любого числа неотрицателен. Решением неравенства будет лишь то значение х, при котором х+4≠ 0, т.е. при х≠-4.

2. Находим производную:

у’=(ln(x+4)² + 2x + 7)’

По свойству логарифма получаем:

у’=(ln(x+4)² )’+(2x)’+(7)’.

По формуле производной сложной функции:

(lnf)’=(1/f)∙f’. У нас f=(x+4)²

у^, = (ln(x+4)² )’+ 2 + 0 = (1/(x+4)² )∙((x+4)²)’ + 2=(1/(x+4)² 2)∙(х² + 8х + 16)’ +2=2(х + 4) /((х + 4)²) + 2

у’= 2/(х + 4) + 2

3. Приравниваем производную к нулю:

у^, = 0 → (2+2∙(х + 4))/(х + 4)=0,

2 +2х +8 =0, 2х + 10 = 0,

2х = -10,

х = -5

Ответ: -5.

Второй вариант задания (из Ященко, №1)

Найдите точку минимума функции y = x – ln(x+6) + 3.

Алгоритм решения:

Определяем область определения функции.
Находим производную.
Определяем, в каких точках производная равна 0.
Исключаем точки, не принадлежащие области определения.
Среди оставшихся точек ищем значения х, в которых функция имеет минимум.
Записываем ответ.

Решение:

1. ОДЗ: .

2. Найдем производную функции:

3. Приравниваем полученное выражение к нулю:

4. Получили одну точку x=-5, принадлежащую области определения функции.

5. В этой точке функция имеет экстремум. Проверим, минимум ли это. При х=-4

При х=-5,5 производная функции отрицательна, так как

Значит, точка х=-5 является точкой минимума.

Ответ: -5.

Третий вариант задания (из Ященко, №12)

Найдите наибольшее значение функции на отрезке [-3; 1].

Алгоритм решения:.

Находим производную.
Определяем, в каких точках производная равна 0.
Исключаем точки, не принадлежащие заданному отрезку.
Среди оставшихся точек ищем значения х, в которых функция имеет максимум.
Находим значения функции на концах отрезка.
Ищем среди полученных значений наибольшее.
Записываем ответ.

Решение:

1. Вычисляем производную от функции, получим

2. Приравниваем производную к нулю:

Решение уравнения дает два корня

- не принадлежит множеству действительных чисел

.

3. Значение и остается одна точка .

4. Вычисляем значения функции в точке -2 и на концах отрезка -3 и 1, получим: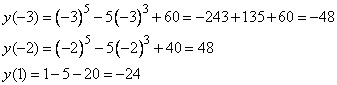

Наибольшее значение функции на заданном отрезке равно 48 в точке х=-2.

Ответ: 48.

Уравнения

В 13 задании профильного уровня ЕГЭ по математике необходимо решить уравнение, но уже повышенного уровня сложности, так как с 13 задания начинаются задания бывшего уровня С, и данное задание можно назвать С1. Перейдем к рассмотрению примеров типовых заданий.

Разбор типовых вариантов заданий №13 ЕГЭ по математике профильного уровня

Первый вариант задания (демонстрационный вариант2018)

а) Решите уравнение cos2x = 1-cos(п/2-x)

б) Найдите все корни этого уравнения, принадлежащие промежутку [-5п/2;-п].

Алгоритм решения:

Пункт а)

При помощи тригонометрических формул приводим уравнение к виду, содержащему только одну тригонометрическую функцию.
Заменяем эту функцию переменной t и решаем получившееся квадратное уравнение.
Делаем обратную замену и решаем простейшие тригонометрические уравнения.

Пункт б)

Строим числовую ось.
Наносим на нее корни.
Отмечаем концы отрезка.
Выбираем те значения, которые лежат внутри промежутка.
Записываем ответ.

Решение:

Пункт а)

1. Преобразуем правую часть равенства, используя формулу приведения cos(π/2−x)=sinx. Имеем:

сos2x = 1 – sin x.

Преобразуем левую часть уравнения, используя формулу косинуса двойного аргумента, с использованием синуса:

cos(2х)=1−2sin² х

Получаем такое уравнение: 1−sin ²x=1− sinx

Теперь в уравнении присутствует только одна тригонометрическая функция sinx.

2. Вводим замену: t = sinx. Решаем получившееся квадратное уравнение:

1−2t²=1−t,

−2t²+t=0,

t (−2t+1)=0,

t = 0 или -2t + 1 = 0,

t₁= 0 t₂= 1/2.

3. Делаем обратную замену:

sin x = 0 или sin x = ½

Решаем эти уравнения:

sin x =0↔x=πn, nЄZ

sin(x)=1/2↔x= (-1)ⁿ∙(π/6)+ πn, nЄZ.

Следовательно, получаем два семейства решений.

Пункт б):

1. В предыдущем пункте получено два семейства, в каждом из которых бесконечно много решений. Необходимо выяснить, какие из них, находятся в заданном промежутке. Для этого строим числовую прямую.

2. Наносим на нее корни обоих семейств, пометив их зеленым цветом (первого) и синим (второго).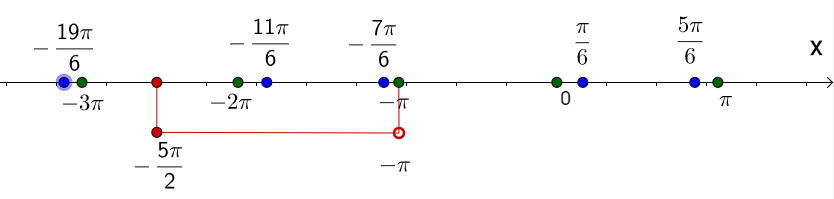

3. Красным цветом помечаем концы промежутка.

4. В указанном промежутке расположены три корня что три корня: −2π;−11π/6 и −7π/6.

Ответ:

а) πn, nЄZ; (-1)ⁿ∙(π/6)+ πn, nЄZ

б) −2π;−11π6;−7π6

Второй вариант задания (из Ященко, №1)

а) Решите уравнение .

б) Найдите все корни этого уравнения, принадлежащие отрезку .

Алгоритм решения:

Пункт а)

Заменяем эту функцию переменной t и решаем получившееся квадратное уравнение.
Делаем обратную замену и решаем простейшие показательные, потом тригонометрические уравнения.

Пункт б)

Строим координатную плоскость и окружность единичного радиуса на ней.
Отмечаем точки, являющиеся концами отрезка.
Выбираем те значения, которые лежат внутри отрезка.
Записываем ответ.

Решение:

Пункт а)

1. Вводим замену t = 4^{cos х}. тогда уравнение примет вид:

Решаем квадратное уравнение с помощью формул дискриминанта и корней:

D=b² – c = 81 – 4∙4∙2 =49,

t₁= (9 – 7)/8= ¼, t₂ = (9+7)/8=2.

3. Возвращаемся к переменной х: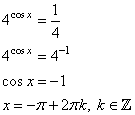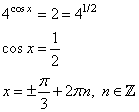

Пункт б)

1. Строим координатную плоскость и окружность единичного радиуса на ней.

2. Отмечаем точки, являющиеся концами отрезка.

3. Выбираем те значения, которые лежат внутри отрезка..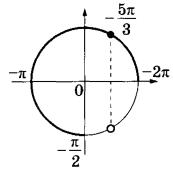

Это корни . Их два.

Ответ:

а)

б)

Третий вариант задания (из Ященко, № 6)

а) Решите уравнение .

б) Найдите все корни этого уравнения, принадлежащие отрезку .

Алгоритм решения:

Пункт а)

При помощи тригонометрических формул приводим уравнение к виду, содержащему только одну тригонометрическую функцию.
Заменяем эту функцию переменной t и решаем получившееся квадратное уравнение.
Делаем обратную замену и решаем простейшие показательные, а затем тригонометрические уравнения.

Пункт б)

Решаем неравенства для каждого случая.
Записываем ответ.

Решение:

а)

1. По формулам приведения .

2. Тогда данное уравнение примет вид:

3. Вводим замену . Получаем:

Решаем обычное квадратное уравнение с помощью формул дискриминанта и корней: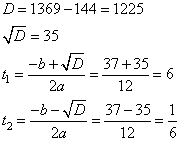

Оба корня положительны.

3. Возвращаемся к переменной х: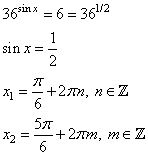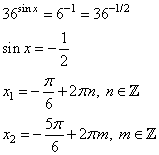

Получили четыре семейства корней. Их бесконечно много.

б)

4. С помощью неравенств находим те корни, которые принадлежащие отрезку :

Для корней



Получаем одно значение .

Для корней     ни одного значения корней нет.

Для корней     есть одно значение ;

Для корней     есть одно значение .

Ответ:

а) ; ;

б) .

1 ... 8 9 10 11 12 13 14 15 16