Разбор вариантов ЕГЭ. Разбор типовых вариантов заданий ЕГЭ по математике_20181010_2236. Двух частей, которые различаются по содержанию, сложности и числу заданий 8 заданий первой части (задания 18) с кратким ответом в виде целого числа или конечной
 Скачать 0.61 Mb. Скачать 0.61 Mb.
|
Текстовые задачиВ задании №11 ЕГЭ по математике профильного уровня требуется решить текстовую задачу. Как правило задача сводится к составлению двух уравнений с двумя неизвестными, которые необходимо выразить, подставить, вычислить и получить ответ! Приступим к разбору, так как какой-либо теории тут нет. Разбор типовых вариантов заданий №11 ЕГЭ по математике профильного уровняПервый вариант задания (демонстрационный вариант 2018)Весной катер идёт против течения реки в 1 2/3 раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в 3/2 раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч). Алгоритм решения:Обозначаем неизвестные скорости переменными х и у. Составляем систему уравнений, исходя из условия. Выражаем х из одного уравнения системы через переменную у. Найденное выражение подставляем в другое уравнение системы и решаем получившееся уравнение. Записываем ответ. Решение:1. Пусть скорость катера равна х км/ч, а скорость течения весной у км/ч. Тогда y–1 (км/ч) – скорость течения летом. Скорость катера по течению весной равна х+у км/ч, а против течения х – у км/ч. Летом соответственно скорости по течению и против равны: х+(у – 1) и х – (у – 1) км/ч. 2. По условию катер идет весной по течению со скоростью, которая составляет 5/3 от скорости против течения. Имеем: х+у=(5/3)(х – у). Летом эти скорости разнятся в 3/2раза. То есть: х+(у – 1)=(3/2)(х – (у – 1). Составим систему уравнений: 3. Выразим x через y из первого уравнения: (5/3)(x–y)=(x+y), (5/3)x – (5/3)y = x + y, –(5/3)y – y = x – (5/3)x, –(8/3)y = –(2/3)x, 8y = 2x, 4y = x, х=4у. 4. Подставляем полученное значение в другое равенство (3/2)(4y–(y–1)) = 4y+(y–1). Отсюда (3/2)(4y–y+1) = 4y+y–1, (3/2)(3y+1) = 5y–, (9/2)y + 3/2 = 5y–1, (9/2)y – 5y = –1 – 3/2, (9/2)y – (10/2)y = –1 – 3/2, –(1/2)y = –5/2, (1/2)y = 5/2, y = 5. Следовательно, скорость течения весной равна 5 км/ч. Ответ: 5. Второй вариант заданияРасстояние между пристанями А и В равно 77 км. Из А в В по течению реки отправился плот, а через 1 час вслед за ним отправилась моторная лодка, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот проплыл 40 км. Найдите скорость моторной лодки в неподвижной воде, если скорость течения реки равна 4 км/ч. Ответ дайте в км/ч. Алгоритм решения:Обозначаем неизвестную скорость переменной х. Составляем уравнение для решения задачи, учитывая условие. Решаем получившееся уравнение. Делаем вывод. Записываем ответ. Решение:1. Пусть скорость лодки равна х км/ч. Тогда ее скорость по течению равна х+4 км/ч, а против течения х – 4 км/ч. 2. Пока лодка шла из точки A к точке B и обратно, плот по течению реки проплыл 40 км. Скорость течения равна 4 км/ч, можно установить, сколько времени двигался плот: 40:4=10 ч. Лодка отправилась в путь на 1 ч позже: 10 – 1= 9 ч. Расстояние в 77 км в направлении течения моторная лодка проплыла за ч, а против течения за ч. Время, которое лодка была в движении туда и обратно равно 9 ч. Получаем уравнение: Упрощаем полученное уравнение, и находим из него х: 77(х – 4)+77(х + 4)=9(х + 4)(х – 4) 77х – 77∙4 + 77х + 77∙4 = 9 (х2 – 16) 154х – 9х2 + 9∙16 – 9х2+ 154х + 144 = 0 9х2 – 154х – 144=0 Решаем квадратное уравнение через дискриминант, получаем: 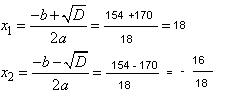 Скорость не может быть отрицательной, тогда второй корень не удовлетворяет условию. Получаем, что скорость моторной лодки равнялась 18 км/ч. Ответ: 18. Третий вариант задания (из Ященко, №31)Из пункта А в пункт В, расстояние между которыми 60 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 30 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 2 часа 40 минут позже автомобилиста. Ответ дайте в километрах в час. Алгоритм решения:Вводим переменную х. Составляем уравнение, исходя из условия. Решаем получившееся уравнение. Делаем вывод. Записываем ответ. Решение:1. Обозначим через х скорость движения велосипедиста. 2. Скорость автомобилиста на 30 км/ч выше, следовательно, она равна х+30. Автомобиль 60 км проезжает за часов, а велосипедист за часов. По условию велосипедист прибыл на 2 часа 40 минут (8/3 часа) позже в назначенный пункт, чем автомобилист. Получаем уравнение 3. Решаем полученное уравнение. Для этого преобразуем его: 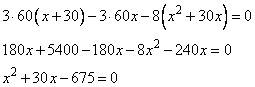 Решаем квадратное уравнение, получаем два корня Скорость не может быть отрицательной, значит, второй корень уравнения не удовлетворяет условию. Значит, велосипедист двигался со скоростью 15 км/ч. Ответ: 15. |
