Разбор вариантов ЕГЭ. Разбор типовых вариантов заданий ЕГЭ по математике_20181010_2236. Двух частей, которые различаются по содержанию, сложности и числу заданий 8 заданий первой части (задания 18) с кратким ответом в виде целого числа или конечной

• Название: Двух частей, которые различаются по содержанию, сложности и числу заданий 8 заданий первой части (задания 18) с кратким ответом в виде целого числа или конечной
• Анкор: Разбор вариантов ЕГЭ
• Дата: 15.03.2022
• Размер: 0.61 Mb.
• Имя файла: Разбор типовых вариантов заданий ЕГЭ по математике_20181010_2236.docx
• Тип: Документы; #398425
• страница: 7 из 16

Производная и первообразные функции

В задании №7 профильного уровня ЕГЭ по математике необходимо продемонстрировать знания функции производной и первообразной. В большинстве случаев достаточно просто определения понятий и понимания значений производной.

Разбор типовых вариантов заданий №7 ЕГЭ по математике профильного уровня

Первый вариант задания (демонстрационный вариант 2018)

На рисунке изображён график дифференцируемой функции y = f(x). На оси абсцисс отмечены девять точек: x₁, x₂, …, x₉. Среди этих точек найдите все точки, в которых производная функции y = f(x) отрицательна. В ответе укажите количество найденных точек.

Алгоритм решения:

1. 
   Рассматриваем график функции.
   
2. 
   Ищем точки, в которых функция убывает.
   
3. 
   Подсчитываем их количество.
   
4. 
   Записываем ответ.
   

Решение:

1. На графике функция периодически возрастает, периодически убывает.

2. В тех интелвалах, где функция убывает, производная имеет отрицательные значения.

3. В этих интервалах лежат точки x₃, x₄, x₅, x₉. Таких точек 4.

Ответ: 4.

Второй вариант задания (из Ященко, №4)

На рисунке изображён график функции у = f(x). На оси абсцисс отмечены точки -2, -1, 2, 4. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.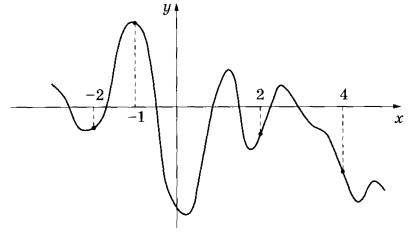

Алгоритм решения:

1. 
   Рассматриваем график функции.
   
2. 
   Рассматриваем поведение функции в каждой из точек и знак производной в них.
   
3. 
   Находим точки в наибольшим значением производной.
   
4. 
   Записываем ответ.
   

Решение:

1. Функция имеет несколько промежутков убывания и возрастания.

2. Там, где функция убывает. Производная имеет знак минус. Такие точки есть среди указанных. Но на графике есть точки, в которых функция возрастает. В них производная положительная. Это точки с абсциссами -2 и 2.

3. Рассмотрим график в точках с х=-2 и х=2. В точке х=2 функция круче уходит вверх, значит касательная в этой точке имеет больший угловой коэффициент. Следовательно, в точке с абсциссой 2. Производная имеет наибольшее значение.

Ответ: 2.

Третий вариант задания (из Ященко, №21)

Прямая    является касательной к графику функции   . Найдите а.

Алгоритм решения:

1. 
   Приравняем уравнения касательной и функции.
   
2. 
   Упрощаем полученное равенство.
   
3. 
   Находим дискриминант.
   
4. 
   Определяем параметр а, при котором решение единственное.
   
5. 
   Записываем ответ.
   

Решение:

1. Координаты точки касания удовлетворяют обоим уравнениям: касательной и функции. Поэтому мы можем приравнять уравнения. Получим:

2. Упрощаем равенство, перенеся все слагаемые в одну сторону:

 

3. В точке касания должно быть одно решение, поэтому дискриминант полученного уравнения должен равняться нулю. Таково условие единственности корня квадратного уравнения.

4. Получаем:



Ответ: 4.

Стереометрия

Задание №8 в профильном уровне ЕГЭ по математике проверяет базовые знания стереометрии. Задания в этом разделе простые, на базовые формулы - обычно на объемы простых стандартных фигур - цилиндра, куба, пирамиды, конуса.

Теория к заданию №8

Приведу формулы объема фигур, так данный материал довольно часто встречается.

Разбор типовых вариантов заданий №8 ЕГЭ по математике профильного уровня

Первый вариант задания (демонстрационный вариант 2018)

В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 2 раза больше первого? Ответ выразите в см.

Алгоритм решения:

1. 
   Определяем площадь основания первого и второго сосудов.
   
2. 
   Записываем формулы объемов и приравниваем их.
   
3. 
   Убираем одинаковые величины. Делаем вывод.
   
4. 
   Записываем ответ.
   

Решение:

1. Площадь основания первого сосуда определяется формулой

Диаметр второго сосуда в 2 раза больше. Значит площадь основания его равна

то есть в 4 раза больше: 

2 Записываем формулы объема жидкости в каждом сосуде.

Так как объем жидкости остается постоянным, получаем уравнение:

Убираем одинаковые величины. Отсюда

Ответ: 4.

Второй вариант задания (из Ященко, №1)

Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 28. Найдите объём цилиндра.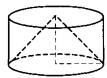

Алгоритм решения:

1. 
   Записываем формулу объема конуса.
   
2. 
   Записываем формулу объема цилиндра.
   
3. 
   Сравниваем формулы, делаем вывод.
   
4. 
   Вычисляем объем цилиндра.
   
5. 
   Записываем ответ.
   

Решение:

1. Объем конуса определяем по формуле

где H – высота конуса; R – радиус основания конуса.

2. Объем цилиндра определяем по формуле

3. Сравниваем обе формулы. Легко видно, что объем цилиндра в 3 раза больше объема конуса.

4. Вычисляем объем цилиндра::

Ответ: 84.

Третий вариант задания (из Ященко)

Диагональ куба равна   . Найдите его объём.

Алгоритм решения:

1. 
   Выражаем диагональ куба, используя теорему Пифагора.
   
2. 
   Решаем полученное уравнение.
   
3. 
   Вычисляем объем.
   
4. 
   Записываем ответ.
   

Решение:

1. По тереме Пифагора диагональ грани куба определяется формулой:

Тогда диагональ куба 

2. Отсюда



3. Объем куба равен

Ответ: 64.