Разбор вариантов ЕГЭ. Разбор типовых вариантов заданий ЕГЭ по математике_20181010_2236. Двух частей, которые различаются по содержанию, сложности и числу заданий 8 заданий первой части (задания 18) с кратким ответом в виде целого числа или конечной
 Скачать 0.61 Mb. Скачать 0.61 Mb.
|
Квадратная решетка и координатная плоскостьВ задании №3 профильного уровня ЕГЭ по математике мы будем работать с фигурами на квадратных решетках - вычислять параметры фигур - стороны или площади, а также расстояния между точками. Приступим непосредственно к разбору типовых вариантов. Первый вариант задания (демонстрационный вариант 2018) На клетчатой бумаге с размером клетки 1х1 изображен треугольник. Найдите площадь. Алгоритм решения: Подсчитываем длину основания и высоты. Записываем формулу вычисления площади. Вычисляем площадь. Записываем ответ. Решение: 1. Подсчитываем длины основания и высоты: основание = 6, высота = 2. 2. Записываем формулу площади треугольника: S= ah|2. 3. Вычисляем площадь: S= 6∙2/2=6 Ответ: 6. Второй вариант задания (из Ященко, №1) На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии этой трапеции. 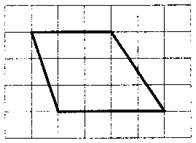 Алгоритм решения: Подсчитываем длину каждого основания и высоты трапеции. Записываем формулу длины средней линии трапеции. Вычисляем среднюю линию. Записываем ответ. Решение: 1. По условию задачи каждая клетка представляет одну единицу длины. Тогда меньшее основание равно 3, большее – 4. 2. Длина средней линии трапеции находится по формуле , где a и b – длина верхнего и нижнего оснований трапеции. 3. Имеем: . 4. Значит, средняя линия равна 3,5. Ответ: 3,5. Третий вариант задания (из Ященко, №2) На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии этой трапеции.  Алгоритм решения: Подсчитываем длину каждого основания и высоты трапеции. Записываем формулу длины средней линии трапеции. Вычисляем среднюю линию. Записываем ответ. Решение: 1. По условию задачи каждая клетка представляет одну единицу длины. Тогда меньшее основание равно 2, большее – 6. 2. Длина средней линии трапеции находится по формуле , где a и b – длина верхнего и нижнего оснований трапеции. 3. Имеем: 4. Значит, средняя линия равна 4. Ответ: 4. Четвертый вариант задания (из Ященко, №4) На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его биссектрисы, проведённой из вершины В. 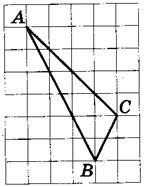 Алгоритм решения: Проведем перпендикуряры из вершин Аи С. Построим биссектрису угла В. Покажем, что биссектриса параллельна высотам. Измерим длину биссектрисы. Запишем ответ. Решение: 1. Проведем из вершин А и С отрезки АВ1 иСВ2, перпендикулярные прямой, содержащей вершину В на рисунке. 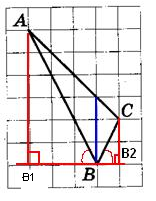 2. Построим биссектрису угла B. 3. Рассмотрим треугольники АВВ1 иВВ2С. Они прямоугольные, тогда из соотношений в прямоугольных треугольниках Это означает, что углы АВB1 и СВB2 равны, так как равны тангенсы этих углов. Раз равны углы, то стороны AB и BC расположены под одним углом относительно вертикали (На рисунке она проведена синим). Эта вертикаль является биссектрисой. Длина биссектрисы по рисунку равна 3. Ответ: 3. Пятый вариант задания (из Ященко, №7) На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь. 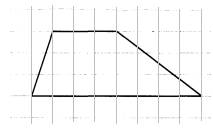 Алгоритм решения: Рассмотрим рисунок и измерим основания. Проведем высоту. Запишем формулу площади трапеции. Вычислим площадь по формуле. Решение: 1. На рисунке основания равны 3 и 8. 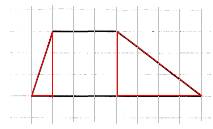 2. Опустим высоту. Она рана 3. 3. Формула трапеции: S=h(a+b)/2, где a,b – основания, h – высота. 4. Вычислим площадь, подставив значения: S=3∙(3+8)/2=16,5 Следовательно, площадь данной трапеции равна 16,5. Ответ: 16,5. |
