пособие. пособие ворд. Федерации по делам гражданской обороны, чрезвычайным ситуациям

• Название: Федерации по делам гражданской обороны, чрезвычайным ситуациям
• Анкор: пособие
• Дата: 18.05.2022
• Размер: 1.05 Mb.
• Имя файла: пособие ворд.docx
• Тип: Документы; #535792
• страница: 21 из 55

Общая (абсолютная) и сравнительная экономическая эффективность капитальных вложений

Общая (абсолютная) эффективность представляет собой отношение эффекта к капитальным вложениям, вызвавшим этот эффект:

Общая (абсолютная) эффективность =

Экономический эффект Капиталовложения ^;

руб./год _{. (6.1)}

руб.

Эта оценка, как правило, сравнивается с заранее установленным нор- мативом. Причем норматив этот может устанавливаться на основе каких- то критериев и приоритетов или приниматься общепринятый в практике проектирования (разработки) системы обеспечения пожарной безопасно- сти. И только после сравнения с заранее установленным нормативом срав- нительной экономической эффективности дополнительных капиталовло- жений (Е_н) принимается решение о выгодности затрат и целесообразности их реализации.

Предположим, что в результате внедрения нового технического реше- ния размер ущерба от пожара уменьшится на величину ∆У, эксплуатаци- онные расходы уменьшились (+) или увеличились (–) на величину ∆С. То-

руб./год

гда показатель эффективности Е_а, _руб. , математически может быть представлен в следующем виде:

Е_а =

У  С К
, (6.2)

где К – капитальные вложения на реализацию технического решения, руб. Если Е_а > Е_н, то предлагаемый вариант принимается к рассмотрению.

Таких вариантов набирается несколько. Из них необходимо выбирать лучший путем сравнения между собой. Такая оценка называется сравни-тельной экономической эффективностью. Для выбора наилучшего вари- анта используются показатели эффективности капитальных вложений в обеспечение пожарной безопасности.

3. Показатели эффективности капитальных вложений

Коэффициент сравнительной экономической эффек- тивности дополнительных капитальных вложений. Сравним между со- бой два варианта противопожарных мероприятий. Первый вариант имеет текущие затраты С₁, ожидаемую величину ущерба У₁ и капитальные вло- жения К₁.

Второй вариант, соответственно, С₂ , У₂ и К₂. Причем К₂ > К₁, а сумма

(С₂ + У₂) < (С₁ + У₁).

Итак, дополнительные капитальные вложения по второму варианту

∆К = (К₂ – К₁) (руб.) приводят к экономии (эффекту) суммы текущих за- трат и ожидаемого ущерба ∆(С + У), руб./год, то есть

∆ (С + У) = (С₁ + У₁) – (С₂ + У₂). (6.3)


Влияние роста капитальных вложений на снижение суммы текущих затрат и ожидаемого ущерба оценивается отношением этого снижения к величине вызвавших его капитальных вложений. Это отношение называют коэффициентом сравнительной экономической эффективности (Е), руб./год

руб. ^,

_{Е =} ^^С+У _ ^{С1  У1}  ^ ^{С2 +У2} 

К К₂  К₁
. (6.4)

Этот коэффициент отражает экономию от снижения, получаемую на каждый рубль капитальных вложений.

Срок окупаемости дополнительных капитальных вложений. Вме-

руб./год

сто Е можно исчислять и обратную величину Т_ок , _руб. , которая полу-

чила название срока окупаемости дополнительных капитальных вложений

_{Т =} ΔК ₌ К₂  К₁

. (6.5)

^{ок Δ}^С+У ^{С +У}  ^ ^{С +У} 

1 1 2 2
В практике проектирования чаще исчисляется срок окупаемости. Это объясняется тем, что выраженный в годах, он более понятен разработчи- кам. Из-за термина «окупаемость» можно предположить, будто данный критерий характеризует срок, в течение которого возвращаются вложен- ные средства. На самом же деле, средства, вложенные в новый вариант противопожарных мероприятий, возвращаются по мере износа их элемен- тов посредством амортизационных отчислений.

Срок окупаемости Т_ок позволяет учесть в экономическом расчете то, что эксплутационные отчисления не учитывают, а именно, – накопления за счет сокращения экономического ущерба. Условие выгодности более ка- питального варианта можно представить в виде следующих неравенств:

_Е  Е_{н }

если _{Т  Т}  , (6.6)

 ок н 

то второй вариант более выгодный, чем первый.

Рассмотрим пример выбора лучшего варианта по сравнительной эф- фективности дополнительных капитальных вложений.

Пусть имеются два альтернативных варианта вложений в противопо- жарные мероприятия. По вариан ту 1 сумма текущих затрат и экономиче- ского ущерба от пожаров за год будет равна: (С₁ + У₁) = 100 тыс. руб./год.

По ва риа н ту 2 тот же показатель – (С₂ + У₂) = 120 тыс. руб./год. Капитальные вложения будут равны соответственно: К₁ = 2000 тыс. руб.

и К₂ = 1900 тыс. руб.

Определяем по исходным данным коэффициент эффективности по формуле

_{Е } 120 100 _ 20


_{ 0, 2} ^ руб./год ^ _{. (6.7)}

2000 1900 100 ^ руб. ^

 

Полученная величина показывает, что дополнительные капиталь- ные вложения в противопожарные мероприятия дадут отдачу в размере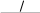

^ руб. год ^

^0,2 

руб.

 ^{экономического эффекта от снижения суммы текущих за-}

 

трат и ущерба на каждый рубль дополнительных вложений. Но данный по- казатель не позволяет определить, какой из двух рассматриваемых вариан- тов будет оптимальным. С этой целью принимаем норматив эффективности Е_н равным 0,15. Тогда в соответствии с формулой (6.4) можно утверждать, что более выгодным будет более капиталоемкий вариант, т. е. в данном

случае ва риа н т 1, так как в соответствии с формулой (6.4) 0,2 > 0,15. Однако, если норматив будет принят на уровне Е_н = 0,25, то более выгод- ным станет менее капиталоемкий вариант, т. е. вар и ант 2.

Из изложенного можно сделать важный вывод: при выборе лучшего варианта из двух рассматриваемых очень большое значение имеет величи- на принятого норматива эффективности дополнительных вложений (Е_н), который является нормой.

В условиях рыночной экономики каждое предприятие, фирма, органи- зация устанавливает для себя значение такого норматива самостоятельно и независимо от других объектов экономики. Эта величина норматива и применяется при расчете экономической эффективности мероприятий в области обеспечения пожарной безопасности данного объекта. Обычно она включает в себя следующие составляющие:

Е_н =Е_г +Е_р +Е_{п , (6.8)}

где Е_н – норматив сравнительной экономической эффективности дополни- тельных капитальных вложений; Е_г – гарантированная норма доходности вложений в высоконадежный коммерческий банк; Е_р – дополнительная страховая норма, учитывающая риск вложения в проект; Е_п – минимальная предельная норма доходности, которая принимается фирмой для положи- тельного решения о дополнительных вложениях в реализацию проекта.

Приведенные затраты. При наличии вариантов больше двух и ис- пользовании коэффициента сравнительной экономической эффективности для выбора наилучшего используют так называемый цепной способ, кото- рый заключается в следующем: выбирают два любых варианта и с помо- щью расчета по формуле (6.6) определяют, какой из них лучше. Затем он сравнивается с любым другим альтернативным вариантом. Отбирают из новой пары опять лучший. Так следует поступать до тех пор, пока не будет найден самый лучший вариант из всех рассматриваемых.

Надо отметить, что такая схема отбора не очень удобна в чисто тех- ническом плане, поскольку очень часто альтернативных вариантов бывает довольно много и процедура выбора наилучшего из них является длитель- ной. Кроме того, в результате такого попарного сравнения теряется очень важная информация о рейтинге каждого из альтернативных вариантов.

Чтобы устранить эти неудобства и придать отбору вариантов капи- тальных вложений в противопожарные мероприятия более объективный характер, нужно иметь более надежный и более простой способ вариантов по отношению к друг к другу. И это оказалось возможным при переходе от показателей формулы (6.6) к другой, которая решает указанные задачи.

Запишем условие выгодности более капитального варианта из двух рассматриваемых. Такое условие можно представить в следующем виде:

_Е= ^С1+У1^^С2+У2 _{ E}

н
. (6.9)

К₂  К₁

После умножения левой и правой части этого неравенства на знаменатель (К₂ – К₁) получаем следующее выражение, которое сохраняет первоначально сформулированное условие о выгодности более капиталоемкого варианта

(С₁+У₁) – (С₂+У₂) > Е_н (К₂ – К₁). (6.10)

Раскроем скобки в правой части представленного выражения и пере- группируем его элементы таким образом, чтобы они были с одинаковыми значениями по разные стороны от знака неравенства. Тогда получим сле- дующее выражение:

С₁ + У₁ + Е_н К₁ > С₂+У₂ + Е_н К₂. (6.11)

Так как данное выражение отражает исходное условие, из которого вид- но, что из двух рассматриваемых вариантов более выгодным является капи- талоемкий, т. е. в данном случае вариант 2, отметим, что именно здесь сум- марные затраты (в правой части неравенства) являются наименьшими. Если бы эти затраты оказались больше, то выгоднее уже был бы менее капитало- емкий вариант. Отсюда можно сделать вывод о том, что во всехслучаяхнаи-более выгодным из множества рассматриваемых вариантов всегда будет тот, у которого суммарные затраты окажутся наименьшими, то есть

П_i C_i У_i E_н К_i min _{. (6.12)}

Последнее выражение получило название приведенныхгодовыхза-трат. Величина П_iимеет размерность руб./год. Она дает обобщенное вы- ражение как капитальным вложениям, так и сумме текущих расходов и ущербу от пожаров, являясь универсальным измерителем.

При П₂ < П₁ получается абсолютная экономия приведенных затрат, названная экономическим годовым эффектом Э_г, руб./год, то есть

Э_г  П₁  П₂  (С₁  У₁  Е_н К₁ )  (С₂  У₂  Е_н К₂ ) _{. (6.13)}

Если в формуле (6.12) обе части умножить на Т_н = 1/Е_н, то получим следующее выражение:

П_ок  П_iТ_н (С_iУ_i)T_н К_{i. (6.14)}

где П_ок, руб., получило название приведенных затрат за период норматив- ного срока окупаемости (Т_н), руб.

При его применении наилучшим вариантом будет тот, у которого его величина будет минимальна. В практике технико-экономических расчетов этот показатель применяется редко.

Применение приведенных годовых затрат на практике сравнения ва- риантов позволяет сформулировать несколько следствий, использование которых позволит упростить процедуру расчетных работ и ускорить отбор лучших вариантов, не теряя точности выводов.

След ст ви е 1. Если рассматриваются между собой варианты, у ко- торых одинаковые капитальные вложения, то лучший вариант будет тот, у которого сумма (С + У) окажется минимальной.

След ст ви е 2. Если рассматриваются варианты, у которых одинако- вые суммы (С + У), то лучший выбирается по минимуму капитальных вло- жений.

След ст ви е 3. Если среди рассматриваемых вариантов имеются одинаковые суммы (С + У) и одинаковые капитальные затраты, то лучший выбирается по минимуму ущерба от пожара.

След ст ви е 4. Если некоторые составляющие величин (К, С, У) в сопоставляемых вариантах будут одинаковыми, то в расчет их можно не принимать. Очевидно, что и указанные выше одинаковые показатели так- же в расчет можно не принимать.