ДИПЛОМНАЯ РАБОТА. Геодезические работы при строительство шиномонтажа и автостоянки для легковых автомобилей

• Название: Геодезические работы при строительство шиномонтажа и автостоянки для легковых автомобилей
• Дата: 10.02.2022
• Размер: 437.65 Kb.
• Имя файла: ДИПЛОМНАЯ РАБОТА.docx
• Тип: Диплом; #357891
• страница: 4 из 5

3.3 Элементы разбивочных работ
Основными элементами разбивочных работ являются построение проектного угла, отложение проектного расстояния, вынесение в натуру проектных отметок и уклонов.

Построение проектного угла. Для построения в натуре проектного угла в от некоторого исходного направления ВА к отсчету по лимбу при визировании по этому направлению прибавляют величину проектного угла. Алидаду устанавливают на полученный отсчет и в створе визирной оси теодолита на соответствующем расстоянии фиксируют на местности точку. Такое же построение выполняют при другом круге, получая на местности вторую точку. Из двух точек берут среднюю С, принимая построенный угол АВС за проектный.

Для повышения точности угловых измерений применяют способ редукции. Угол АВС измеряют несколькими приемами, определяя ее более точную величину в'. Взяв разность между проектным значением в и измеряемым в', находят угловую поправку в, в которую вводят путем отложения в натуре линейного отрезка _l, вычисленного по формуле
_l = l ,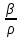
где l – расстояние ВС; с – в угловых секундах.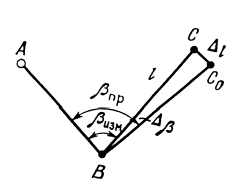


Схема построения проектного угла
Отложение проектных расстояний. Для построения на местности проектной линии от исходной точки откладывают в заданном направлении проектное расстояние, горизонтальное проложение которого равно проектному значению. Поправки в линию необходимо вводить непосредственно в процессе ее построения, а это затрудняет и осложняет работу, особенно при высокоточных измерениях. Поэтому часто поступают таким же образом, как и при построении углов.

На местности откладывают и закрепляют некоторое проектное расстояние. Это расстояние с необходимой точностью измеряют компарированными мерными приборами или точными мерными приборами или точными дальномерами с учетом всех поправок измерений. Получив после камеральной обработки длину закрепленного отрезка и сравнив ее с проектным значением, находят линейную редукцию _l, которую и откладывают с соответствующим знаком от конечной точки отрезка В', находят проектную линию АВ.

Следует иметь в виду, что при непосредственном отложении в натуре проектных расстояний поправки за компарирование, температуру и наклон местности имеют знаки, обратные тем, которые вводят при измерении линий.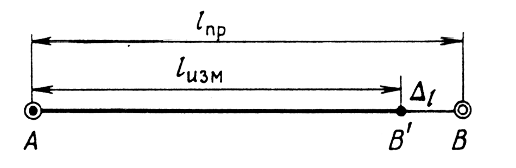


Схема построения проектной линии
Вынесение в натуру проектных отметок. Для вынесения в натуру проектные отметки в рабочих чертежах от условного уровня перевычисляют в абсолютную систему высот, в которой даны отметки реперов и произведена съемка рельефа площадки. На местности от 2 – 3 ближайших реперов определяют горизонт нивелира.
Н_j = Н_рп + а,
где Н_рп – высота репера; а – отчет по рейке, установленной на репере.

Предвычисленный отсчет b по рейке получают как разность среднего горизонта прибора H_jср и проектной высоты точки H_пр:
b = H_jср – H_пр

Поднимая или опуская рейку в точке на проектной поверхности, добиваются, чтобы средняя нить нивелира показала отсчет. Тогда пятка рейки будет фиксировать проектную высоту.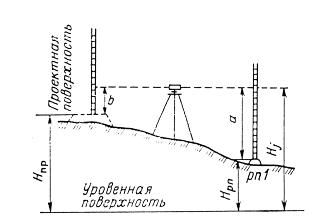


Схема выноса проектной отметки
Вынесение в натуру линий и плоскости заданного уклона. Для построения на местности проектных линий и плоскостей используют нивелиры и теодолиты. Особенно эффективно применять для этой цели лазерные приборы.

Нивелир устанавливают так, чтобы два подъемных винта были параллельны линии АВ. Определив горизонт инструмента, устанавливают в натуре проектные отметки точек А и В. Наклоняя нивелир двумя подъемными винтами, добиваются, чтобы отсчеты по рейкам, установленным на проектных отметках в точках А и В, были одинаковы, т.е. чтобы линия визирования нивелира стала параллельной проектной линии. Если теперь установить рейку в любой точке створа АВ и, поднимая или опуская ее, добиться, чтобы отсчет по ней был равен отсчету на конечных точках А и В, то пятка этой рейки будет фиксировать линию заданного уклона.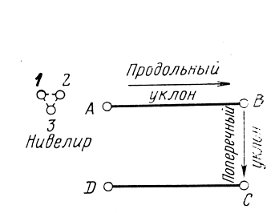


Схема выноса в натуру плоскости
Перевычисление координат. Для увязки в единой системе разбивочных и съемочных сетей площадок и трасс производят перевычисление условных (строительных) координат в государственные по формулам
x = a + x'v cosи – y'v sinи;

y = b + x'v sinи + y'v cosи,
где x и y – прямоугольные координаты пунктов в государственной системе; x' и y' – координаты тех же пунктов в строительной системе; a и b – координаты условного начала в государственной системе; v – коэффициент изменения масштаба сети в связи с редуцированием на плоскость проекции Гаусса и приведением к поверхности эллипсоида Красовского; и – разность дирекционных углов соответствующих направлений в государственной и строительной системах координат.

Для упрощения вычислений целесообразно начало строительных координат совмещать с пунктом, координаты которого известны в государственной системы.

Особенности проектирования. Разбивочная основа развивается на строительной площадке для перенесения в натуру главных осей сооружений, их периодического восстановления и уточнения в процессе строительства, а также как опора для сгущения геодезического обоснования при исполнительных съемках, наблюдениях за деформациями и другими работами в период эксплуатации сооружения.

Схема построения разбивочной основы тесно увязывается с генеральным планом сооружения. Геодезические пункты располагают в наиболее устойчивых местах, где бы они сохранились по возможности на весь период строительства и могли бы быть с максимальной эффективностью использованы для разбивочных работ и исполнительных съемок. Разбивочную сеть проектируют как локальную с размещением ее основной стороны параллельно главной разбивочной оси, которую принимают за ось абсцисс. Начало системы выбирают с таким расчетом, чтобы координаты всех точек проекта выражались положительными значениями. В качестве поверхности относимости принимают средний уровень строительной площадки или уровень наиболее ответственных сооружений. В зависимости от типа сооружений разбивочную основу строят в виде сетей триангуляции, строительной сетки, высокоточной микротрилатерации, линейно-угловых построений и полигонометрии. Полигонометрические ходы часто используют для контроля вынесения в натуру главных осей и красных линий застройки. Проложив по вынесенным точкам ходы дальномерной, короткобазисной или светодальномерной полигонометрии, определяют фактические координаты этих точек. Сходимость полученных координат с проектными подтверждает правильность выполненной разбивки и служит основанием для производства детальных разбивочных работ.
3.4 Способы разбивки основных осей сооружения
Способы разбивки сооружений. В зависимости от типа сооружений, условий измерений и требований к точности разбивка может быть произведена различными способами:

– угловой засечкой или замкнутого треугольника;

– способом полярных и прямоугольных координат;

– линейной и створной засечкой.

Угловую засечку применяют главным образом для разбивки мостовых переходов и гидротехнических сооружений. В этом способе положение проектной точки на местности находят, одновременно откладывая теодолитами на пунктах углы в₁ и в₂.

Базисом засечки служит или специально измеренная сторона, или сторона триангуляции (полигонометрии). Разбивочные углы в₁ и в₂ вычисляют как разность дирекционных углов сторон. Последние находят из решения обратной геодезической задачи по проектным координатам разбиваемой и известным координатам исходных пунктов.

На точность разбивки сооружения способом прямой засечки влияют ошибки собственно прямой засечки m_з, исходных данных m_и, центрирования и редукции m_ц,р, фиксации разбиваемой точки на местности m_ф: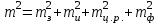

Средняя квадратическая ошибка прямой угловой засечки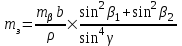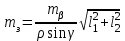



где m_в - средняя квадратическая ошибка отложения углов в₁ и в₂.

По осям координат ошибка засечки выражается формулами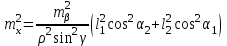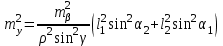



Из формулы относительная ошибка засечки при l₁ ≈ l₂ = l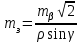

При заданной ошибке m_в относительная ошибка засечки будет минимальна при угле г = 90°. Абсолютная величина ошибки засечки зависит не только от угла г, но и от расстояния до определяемой точки l. Чем больше это расстояние, тем больше будет линейная величина угловой ошибки. С учетом влияния угла г и расстояния l абсолютная ошибка засечки будет минимальна при г = 109° 28'.

Ошибки исходных данных m_и являются следствием ошибок в положении пунктов 1 и 2 разбивочной основы. При независимом определении этих ошибок, приняв m₁≈ m₂= m_1,2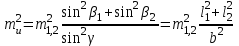

При корреляционной зависимости этих ошибок, что обычно имеет место на практике,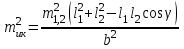

Для случая l₁ = l₂ = l и г = 90є для обоих формул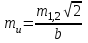

Аналогично формуле совместное влияние ошибок центрирования и редукции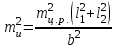

где m_ц,р – средняя квадратическая величина центрирования и редукции.

Ошибка фиксирования определяемой точки зависит от способа проектирования визирной цели, установленной на некоторой высоте над поверхностью земли или сооружения на знак крепления, и от способа обозначения полученной точки на головке этого знака. Применяя марки с оптическими центрами и производя тщательное кернение. Можно зафиксировать точку на металлической головке с ошибкой не более 1 – 2 мм. При употреблении нитяных отвесов эта ошибка увеличивается до 3 – 5 мм.

Способ замкнутого треугольника. Для уточнения разбивки точки прямой засечкой применяют способ замкнутого треугольника. В этом способе после определения в натуре точки С на пунктах 1 и 2 измеряют точное значение отложенных углов в₁ и в₂. затем теодолит устанавливают в точке С и измеряют третий угол г. Распределив невязку в треугольнике поровну или в соответствии с весами измерения углов, определяют координаты точки разбивки С. Сравнивая их с проектными значениями, находят поправки (редукции), по которым разбиваемую точку смещают в натуре в проектное положение.

Для оценки точности определения точки С треугольника может быть рекомендована формула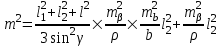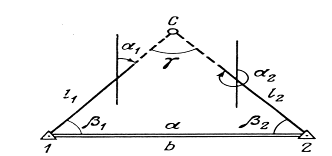



Схема определения положения проектной точки способом замкнутого треугольника
Способ полярных координат. Этот способ применяют главным образом для разбивки точек сооружений с пунктов полигонометрии. Искомую точку С определяют на местности с пункта 1 путем построения полярного угла в и отложения проектного расстояния l.

Точность разбивки точки способом полярных координат определяют по формуле: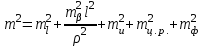
,
где m_l – ошибка отложения расстояния l; m_в – ошибка построения угла в.

Ошибки центрирования и редукции непосредственно не влияют на точность отложения полярного угла, но вызывают смещение разбиваемой точки С.
Совместное влияние этих ошибок определяют по формуле: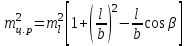

Из формулы видно, что влияние ошибки центрирования и редукции зависит от величины полярного угла в. Это влияние будет наименьшим при угле, близком к 0, и наибольшим при угле около 180°. При разбивке сооружений следует стремиться так выбрать опорные пункты, чтобы угол в на превышал 90° и чтобы откладываемое расстояние не превышало длины исходной стороны (l≤b).

Влияние ошибок исходных данных, т.е. ошибок во взаимном положении смежных пунктов полигонометрии, от которых выносятся в натуру ось сооружения, с учетом их корреляционной связи может быть определено по приближенной формуле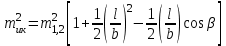

Для полигонометрии 1 разряда m_1,2 ≈ 10 мм, 2 разряда – m_1,2 ≈ 20 мм.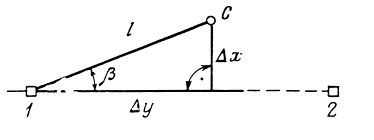


Схема способа полярных координат
Если определяемая точка находится на значительном расстоянии от пункта геодезической основы, то приходиться многократно откладывать запроектированные углы и расстояния, создавая в натуре проектный ход или полигон с измерением примычных углов г и г'. Ошибки в положении конечных точек I и II таких ходов могут быть подсчитаны по формуле сдвига вытянутого полигонометрического хода.

Ошибка взаимного положения точек I и II, определяемых этим способом от опорных пунктов 1 и 2,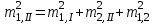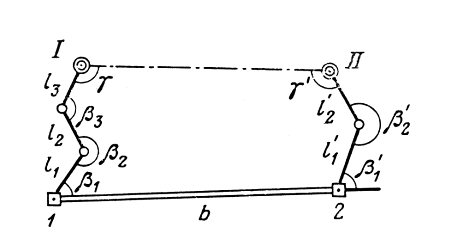



Схема построения проектного полигона
Способ прямоугольных координат. Этот способ применяется при наличии на площадке строительной сетки, в системе координат которой задано положение всех главных точек и осей проекта. Вычислив от ближайшего пункта приращения координат x и y, откладывают от него приращение по соответствующей стороне сетки. В найденной точке (в створе пунктов сетки) устанавливают теодолит и строят от стороны сети прямой угол. По перпендикуляру откладывают меньшее значение приращения и закрепляют полученную точку. Средняя квадратическая ошибка в положении определяемой точки этим способом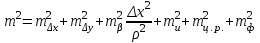


где m_x, m_у – ошибки отложения приращений координат; m_в – ошибка построения прямого угла (если по перпендикуляру откладывается ордината, то в формуле вместоx берут y).

Для соседних пунктов строительной сетки ошибка исходных данных составляет 10 – 20 мм.

Влияние ошибки центрирования и редукции в способе прямоугольных координат можно определить по формуле, заменив стороны l и b соответствующими приращениями координат, и принять в = 90°.

Линейная засечка. Точки сооружения С и D определяются на местности пересечением проектных расстояний l₁ и l₂, отложенных с конечных пунктов 1 и 2 базисной линии. Для контроля сторону СD измеряют и сравнивают с ее проектным значением.

Следует иметь в виду, что для разбивочных работ способ линейной засечки может быть использован только при условии, если проектные расстояния l₁ и l₂ меньше длины применяемых мерных приборов. При отложении проектных расстояний светодальномерами задача решается методом приближений.

Точность линейной засечки определяют по формуле: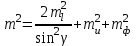

где m_l – ошибка отложения расстояний l₁ и l₂; г – угол при засекаемой точке.

Абсолютная и относительная ошибки линейной засечки минимальные при угле г = 90°. Влияние ошибки m_1,2 взаимного положения исходных пунктов на точность засечки определяется из выражения: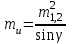

Фиксирование засекаемой точки на знаке крепления может быть выполнена с точностью 1 – 2 мм.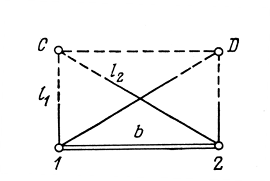


Схема разбивки сооружения способом линейной засечки
Створная засечка. Положение точки на местности этим способом определяется пересечением двух створов (осей), закрепленных на противоположных сторонах сооружения. Створы обычно задаются теодолитами.

Створную засечку преимущественно применяют на разбивке промышленных и гражданских сооружений, где, как правило, оси пересекаются под прямыми углами.

Точность створной засечки зависит от точности построения первого m_С1 и второго m_С2 створов, влияния ошибок исходных данных m_и, а так же от точности фиксирования найденной точки на местности m_ф: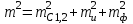

Основными ошибками при построении створов являются ошибки центрирования и редукции m_ц,р, визировании m_в, за изменения фокусировки визирной трубы m_фок, за влияние внешних условий m_вн: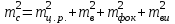


Влияние на точность построения створа ошибок центрирования и редукции выражается формулами: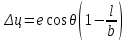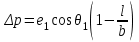



Наибольшая величина ошибок ц и р будет при угловых элементах и и и₁, равных 0 или 180°, и, следовательно, теодолит и визирные цели необходимо центрировать особо тщательно в направлениях, перпендикулярных к створу. Влияние линейной ошибки центрирования l будет увеличиваться по мере приближения к теодолиту. Наоборот, влияние ошибки редукции е₁ будет возрастать с удалением от теодолита и приближением к визирной цели.

Средняя квадратическая ошибка построения створа, вызванная совместным влиянием центрирования и редукции,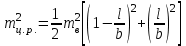

Для теодолита и визирных марок с оптическими центрами величина m_е равна 0,5 – 0,7 мм. Для нитяного отвеса она составляет в закрытых помещениях 2 – 3 мм, на открытых площадках 3 – 5 мм.

Ошибка визирования в створовых измерениях влияет дважды: при ориентировании теодолита по конечной исходной марке и при введении в коллимационную плоскость зрительной трубы наблюдаемой цели. В обоих случаях угловая величина этой ошибки примерно одинаковая. При благоприятных условиях видимости ее среднее квадратическое значение: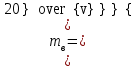

где х – увеличение прибора.

Совместное влияние этих двух ошибок визирования на положение наблюдаемых точек створа в линейной мере составит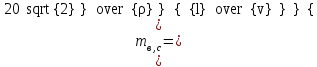

где l – расстояние от теодолита до наблюдаемой точки створа.

При створовых засечках приходится визировать на точки, расположенные на весьма различных расстояниях, и менять фокусировку зрительной трубы. Передвижение фокусирующей линзы вызывает некоторое смещение визирной оси теодолита относительно ее начального положения, что приводит к ошибкам в построении створа. Для уменьшения влияния перемены фокусировки створ следует задавать при двух положениях круга теодолита. В современных точных оптических теодолитах ошибка за перемену фокусировки обычно не превышает ошибки визирования. С учетом этого, общую ошибку визирования на створе можно принять: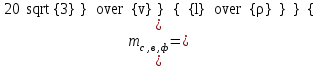

Значительное влияние на точность разбивки сооружений всеми способами особенно створной засечкой оказывают внешние условия (боковая рефракция). Следует стремиться, чтобы линия визирования проходила не ближе 1 м от стен и боковых граней сооружения. Створы необходимо проверять в пасмурные дни или ночное время.

Ошибками исходных данных здесь являются поперечные ошибки в положении знаков, закрепляющих створ. Они зависят от принятой точности

разбивки осей на обноске. Смежные оси откладывают с ошибкой порядка 1 – 2 мм.

При независимом определении исходных данных продольных и поперечных створов общая ошибка в положении разбиваемой точки под влиянием ошибок исходных данных выражается формулой: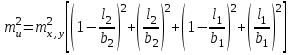

где принято m_х≈ m_у≈ m_х,у.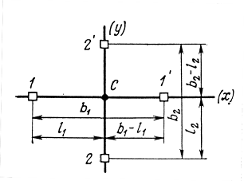


Схема определения расположения проектно точки методом створной засечки
Створно-линейный способ. В этом способе проектные расстояния откладывают по закрепленному створу. Створ задают теодолитом; проектные расстояния (горизонтальные проложения) отмеряют стальным или инварным мерными приборами, точными светодальномерами, последовательно фиксируя положение створных осей.

Точность этого способа зависит от точности построения створа m_с, точности линейных измерений по створу m_l и точности фиксирования разбиваемой точки m_ф: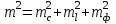

Ошибка разбивочных работ зависит от способа построения в натуре проектных линий и углов, т.е. от геометрии разбивки сооружения. Ожидаемая величина этой ошибки может быть вычислена по известным в геодезии формулам.

Ошибка фиксирования разбиваемой точки определяется методом проектирования визирной цели, установленной на некоторой высоте над поверхностью земли или сооружения, на знак крепления оси и способом обозначения разбиваемой точки на головке этого знака. Применяя визирные марки с оптическими центрами и произведя тщательное кернение, можно зафиксировать точку на металлической головке со средней точностью около 1 мм.

При использовании нитяных остроконечных отвесов эта ошибка увеличивается в закрытых помещениях до 2 – 3 мм, а на открытой местности при ветре до 3 – 2 мм. При детальной разбивке осей, когда в теодолит видна головка закрепляемого знака, в качестве визирной цели часто устанавливают на знак карандаш, гвоздь. Шпильки. В этом случае можно добиться точности фиксирования 1,5 – 2 мм. Таким образом, величина ошибки фиксирования может быть заранее установлена в проекте производства геодезических работ и учтена при расчетах разбивки сооружения.

Влияние ошибок исходных данных, т.е. ошибок в положении опорных пунктов, на точность разбивочных работ является наиболее сложным вопросом, требующим особых исследований.