Грузоведение. Сохранность и крепление грузов. Грузоведение сохранность и крепление грузов
 Скачать 3.03 Mb. Скачать 3.03 Mb.
|
Рассмотренная методика позволяет обеспечить поперечную устойчивость грузов в вагонах при -наиболее неблагоприятном сочетании действующих на груз инерционных и удерживающих сил с учетом содержания пути и подвижного состава. Силы трения и ветровая нагрузка. Поступательному перемещению груза по поверхности вагона или других грузов препятствует сила трения, которая зависит от многих факторов, в том числе от состояния, размеров и температуры соприкасающихся поверхностей, давления, скорости перемещения. Сопротивление, возникающее при перемещении груза по полу вагона, зависит не только от материалов соприкасающихся поверхностей груза и вагона, но и в значительной степени от их состояния: загрязненности, покрытия смазкой и др. Загрязнение соприкасающихся поверхностей смазочными маслами, жирами, мазутом, а также их увлажнение и обледенение резко понижают силу трения. Посыпка поверхностей песком, шлаком, наоборот, увеличивает силу трения. В связи с этим следует тщательно очищать поверхности груза и пол вагона от грязи, смазки и посыпать их песком, металлическими опилками, дробленым шлаком, а также использовать другие средства — шлифовальные шкурки, металлические пластины с шипами, увеличивающие трение между грузом и полом вагона. Силу трения определяют умножением коэффициента трения на массу груза. Однако значения коэффициента трения скольжения, приводимые в различных справочниках, не учитывают особенностей перевозки грузов железнодорожным транспортом, когда в условиях одной перевозки контактирующие поверхности вагона и груза могут иметь различную влажность и подвергаться воздействию положительных и отрицательных температур. Нормативные значения коэффициента трения для «различных пар трения применительно к условиям перевозок грузов устанавливают на основе лабораторных и натурных испытаний. Ветровая нагрузка, испытываемая грузом, зависит от скоростного напора воздуха, размеров поверхности груза и ее состояния. В расчетах крепления груза действие ветра учитывается только в направлении поперек пути. При этом ветровая нагрузка принимается нормальной к поверхности груза и определяется из расчета давления ветра 500 Н/м2. Определение сил, действующих на груз. Продольные, поперечные, вертикальные инерционные силы, силы давления ветра и силы трения во время перевозки достигают максимальных значений неодновременно. По этой причине силы, действующие на груз при перевозке, учитывают в расчетах крепления в двух сочетаниях: первое соответствует ударному взаимодействию вагонов при маневрах, роспуске с горок, трогании, осаживании и торможении поездов при малых скоростях движения, а второе — движению поезда с наибольшей допускаемой на сети железных дорог скоростью, В первом сочетании учитывается действие на груз продольных 187 инерционных сил и сил трения, а во втором — поперечных и вертикальных инерционных сил, ветровой нагрузки и сил трения. Для определения сил, действующих на грузы различных массы и размеров, установлены удельные значения сил: инерционных — на 1 ф груза, силы ветра — на 1 м2 поверхности, подверженной его воздействию. Точкой приложения продольных, поперечных и вертикальных инерционных сил является ЦМ груза, точкой приложения ветровой нагрузки — центр тяжести площадки, подверженной воздействию силы ветра. Продольную инерционную силу, действующую на груз, определяют где аПр — удельная продольная инерционная сила. Ее нормативы утверждены МПС для различных типов крепления и основных видов подвижного состава. Поперечную инерционную силу с учетом действия центробежной силы вычисляют 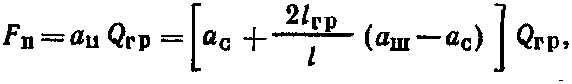 где йи, аСг аш — удельная поперечная инерционная сила, если ЦМ груза расположен соответственно в вертикальных плоскостях, в плоскостях, проходящих через середину вагона и шкворневую балку. Нормативные величины аси ашутверждаются МПС для максимальных скоростей поездов с учетом типа тележек вагонов; / — база вагона, м; /гр — расстояние между ЦМ груза и вертикальной плоскостью, в которой находится поперечная ось вагона, м. Вертикальную инерционную силу определяют где ав — удельная вертикальная сила, определяемая для четырехосных вагонов на тележках ЦНИИ-ХЗ. При скорости 90 км/ч 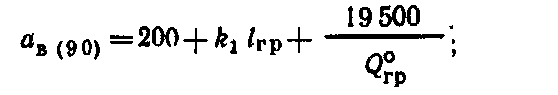 при скорости 100 км/ч 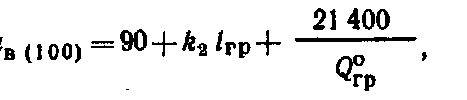 где k\, k2—коэффициенты, зависящие от способа размещения груза, скорости движения вагонов (&й=9 З, k2=\QH); Qrp— общий вес груза в одном вагоне, кН. При загрузке в четырехосный вагон менее 100 кН груза Q°p = 100 кН. Ветровую нагрузку определяют 188 где К — аэродинамический коэффициент, учитывающий степень обтекаемости груза воздухом (для плоских поверхностей /С= I, для цилиндрических К=0,5); q— расчетное давление ветра, принимается равным 500 Н/м2; Sa— площадь проекции поверхности груза, подверженной воздействию ветра , на вертикальную плоскость, проходящую через продольную ось вагона, м2. , Силу трения определяют: при первом сочетании при втором сочетании где м — коэффициент трения. 5.2. Динамика грузов при маневровых соударениях вагонов Влияние числа набегающих и стоящих вагонов на ускорение грузов. Наиболее неблагоприятные воздействия грузы испытывают при соударениях вагонов во время маневров и при роспуске с горок. Качественная и количественная оценки возникающих в этих условиях «инерционных сил и перемещений грузов имеют важное значение для решения вопросов, связанных с обеспечением устойчивости и сохранности вагонов и грузов. Вагон, состоящий из кузова с грузом, тележек и междувагонных связей, представляет динамическую систему со многими степенями свободы. В процессе соударения вагон совершает сложные пространственные колебания, которые обусловлены в основном -наличием поглощающих аппаратов и тележек, оборудованных рессорным подвешиванием. Эта сложная система в исследованиях динамики вагонов заменяется обычно более простой расчетной схемой с ограниченным числом степеней свободы, но в соответствии с поставленными целями отражающей основные ее свойства. Взаимодействие грузов и вагонов при соударениях вагонов (рис. 5.4) для исследования их ускорений и перемещений описывается системой нелинейных дифференциальных уравнений, число которых в зависимости от поставленных задач и принятой идеализации может достигать нескольких десятков. При разработке расчетных схем и составлений математических моделей исходим из того, что принимаемая идеализация должна способствовать изучению основных вопросов, поставленных перед исследованием, т. е. ускорений и перемещений грузов. Большинство применяемых на практике способов размещения и крепления различных грузов может быть представлено следующими схемами: 1-я — одноярусная, когда каждый груз имеет с ва- 189 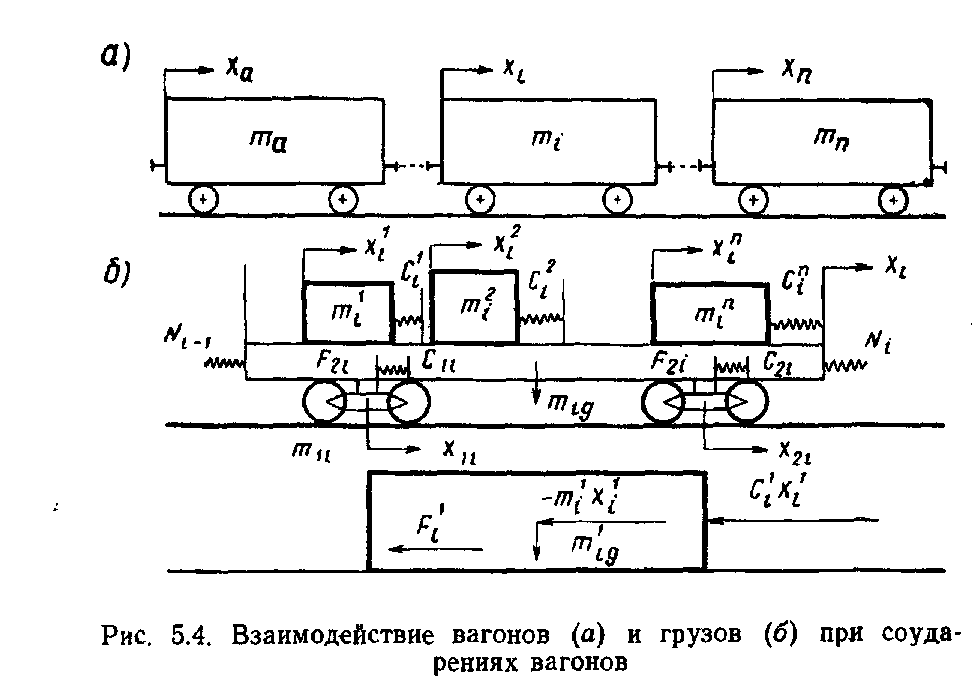 гоном связи упругие и посредством трения; 2-я—одноярусная» когда грузы размещены по длине вагона вплотную друг к другу с упором в торцовые части вагона и имеют с вагоном при продольном перемещении одну упругую связь и каждый груз — связь посредством трения; 3-я — штабельная, когда грузы уложены друг на друга; 4-я и 5-я — одноярусное размещение длинномерного груза с опорой на два вагона с помощью подвижного и неподвижного турникетов (схема 4) и турникетов с наклонными поверхностями скольжения (схема 5). Для разработки расчетных схем вводим следующие ограничения: представляем грузы, рамы и тележки вагонов в виде абсолютно твердых тел; железнодорожный путь горизонтальный; центры масс грузов, рам и тележек вагонов перемещаются по параллельным прямым, зазоры в междувагонных связях не учитываются. Дифференциальные уравнения для случаев размещения в вагонах различных грузов, в том числе длинномерных на сцепах вагонов, составляем с использованием способа Даламбера и уравнений Лагранжа второго рода, представляемых в следующем виде: 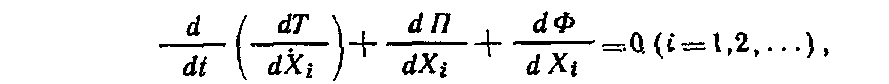 где Ф и Р — кинетическая и потенциальная энергия системы; Ц — диссипативная функция рассеивания. Рассмотрим общий случай взаимодействия вагонов с размещенными на них грузами. Движение вагона и перемещение лрузов в них описываются системой нелинейных дифференциальных урав- 190 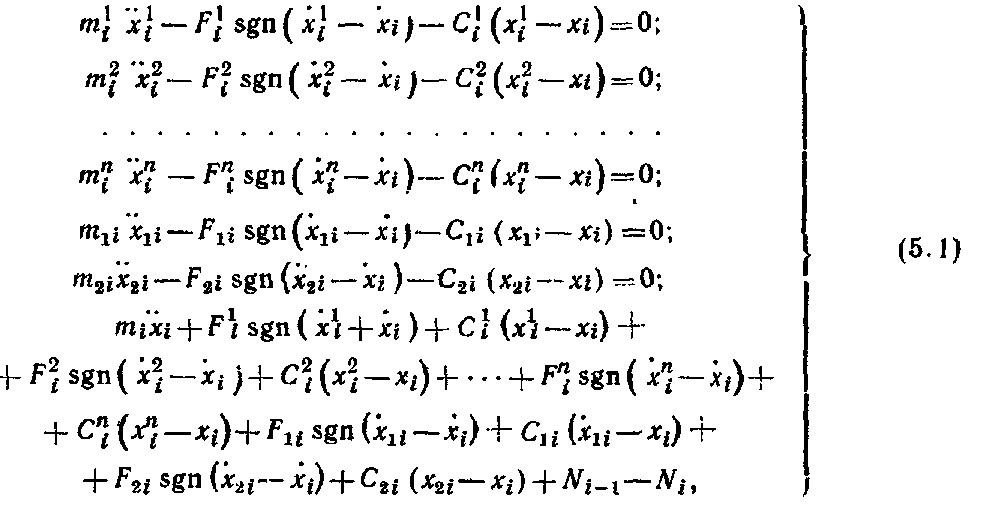 нений. Для любого i-ro вагона система уравнений может быть представлена: где tnf,mj /и", —массы соответственно грузов, тележек и рамы вагона; щи, гпги trii ч), ч*> ..,, xf, —продольные горизонтальные перемещения соответственно хи, Хги Хх центров масс грузов, тележек и рамы вагона; С J. CJ, ..., С\, —соответственно жесткости соединения грузов и тележек с С/, dрамой вагона; Fj, Ff, ..., F*} — силы трения между грузами и вагоном; Fu, Fm— силы трения между рамой и тележками; JVf-ь Ni— усилия в междувагонных связях. 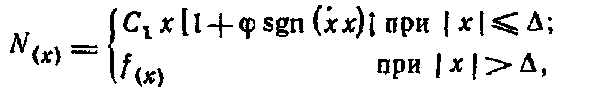 где f(x) — усилие в междувагонной связи при жестком соударении вагонов: 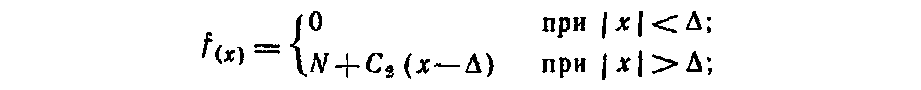 Для междувагонных связей с пружинно-фрикционными поглощающими аппаратами силовая характеристика имеет вид: ч — перемещение вагона за счет деформации междувагонной связи; ц — коэффициент относительного трения; Си Сг — соответственно жесткости междувагонной связи и конструкции рамы вагона; Д — ход поглощающего аппарата вагона. Усилия в связях грузов с вагонами и между грузами, а также в междувагонных связях зависят от относительного движения грузов и вагонов. Поэтому систему уравнений (5.1) следует преобразовать для определения относительных перемещений и скоростей грузов и вагонов. Рассмотрим случай взаимодействия четырех вагонов (а, б, в, г), например, при соударении одного вагона с группой из трех стоящих сцепленных между собой вагонов. Расчетами, результаты которых приведены ниже, установлено, что дальнейшее увеличение числа стоящих вагонов не оказывает практически никакого влияния на значения ускорений и перемещений грузов на набегающем вагоне. Вводим следующие обозначения: 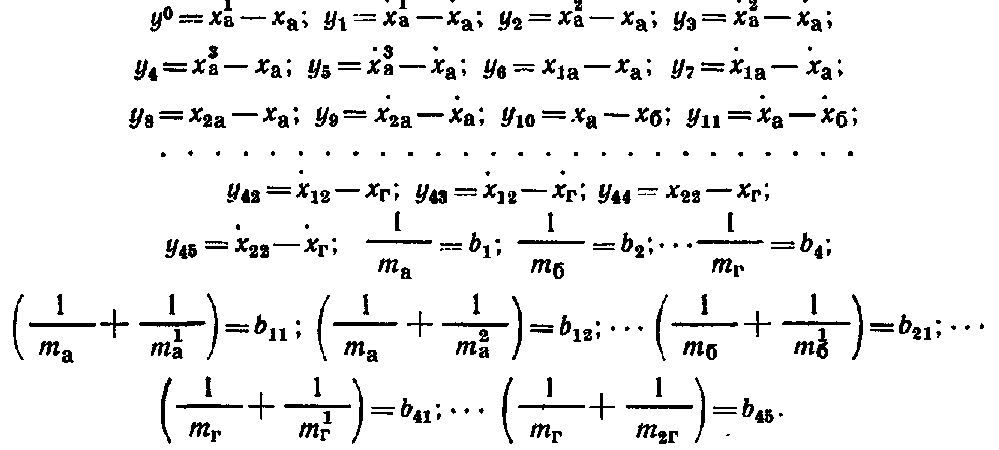 Получаем систему уравнений первого порядка, описывающую относительные движения грузов и вагонов: 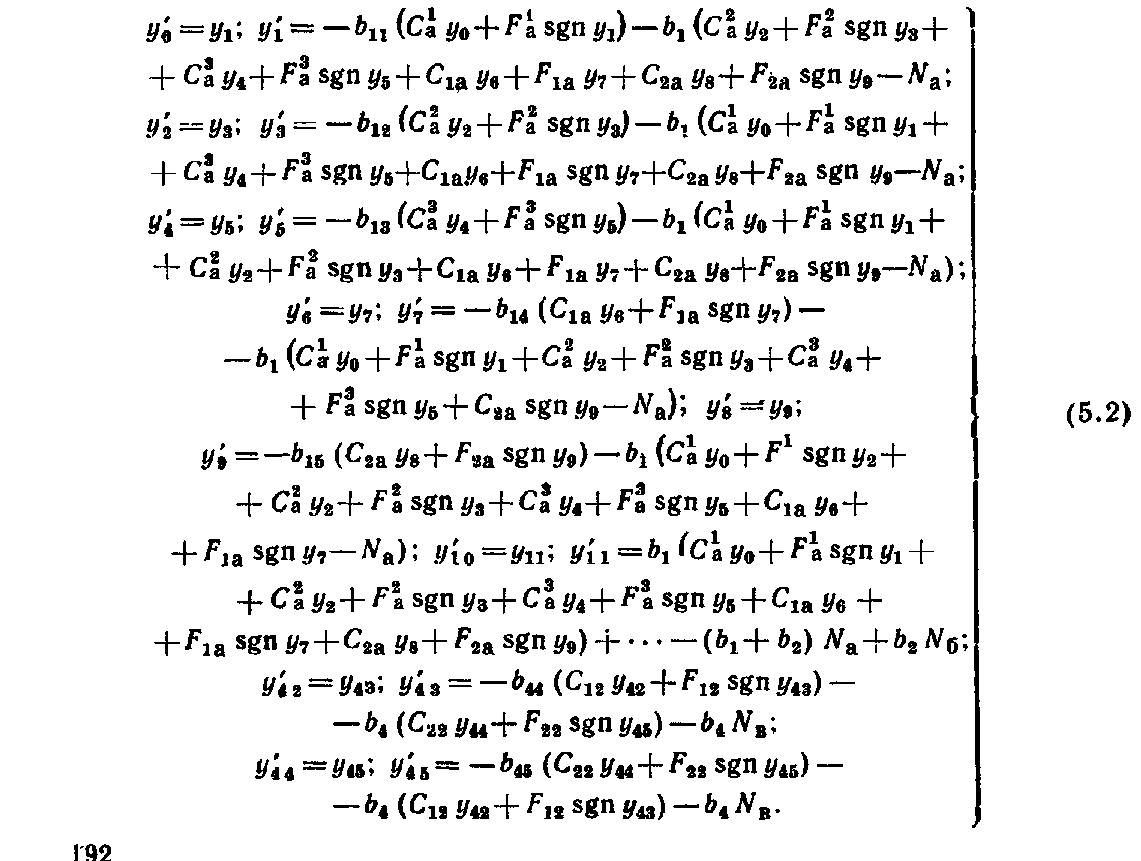 Усилия, действующие «а вагоны и грузы со стороны междувагонных связей, являются функцией времени /, у и //, и решение системы уравнений (5.2) сводится к определению в каждый момент времени относительных перемещений, которые затем используют для вычисления сил и ускорений. Системы ура'внений для исследования поведения грузов в вагонах при их соударении решаем численным интегрированием. Начальные условия: Я=0; скорость набегающего вагона х\ все остальные значения равны нулю. Процесс соударения применительно к поведению груза можно рассматривать состоящим из нескольких этапов. Вначале груз удерживается от перемещений силами трения. В некоторый момент времени t\ сила инерции становится больше удерживающей силы F, и груз начинает перемещаться. Момент начала движения определяется из условия ЧГс·(Я\)>м§* При наличии крепления в этот момент происходит нарастание силы упругого взаимодействия Р, которое прекращается по достижении грузом в момент времени Я2 максимального перемещения. Если в этот момент сила С превышает значение силы трения F, начинается движение груза в противоположную сторону под действием силы Р. Если же F>P, движение груза прекращается. Для решения вопросов крепления грузов при соударениях вагонов определяется максимальное значение ускорений грузов, которое соответствует моменту времени t2: j=xrp=—[\ng-\-CrvlmTP(xTp— Отношение Сгр/тГр является основным показателем жесткости связи груза с вагоном, определяющим частоту колебаний груза относительно вагона усгр/тгр. Для большинства креплений грузов, применяемых на сети железных дорог, это отношение находится в пределах 170—1200 с-2. 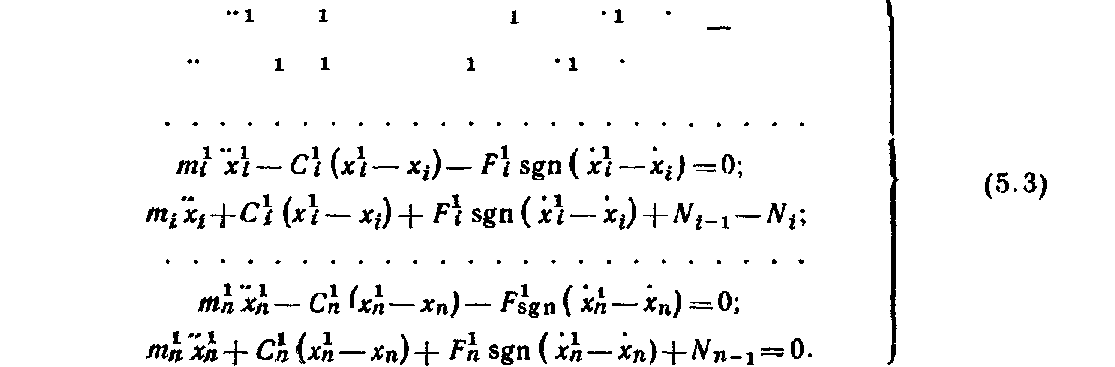 Для изучения влияния числа набегающих и стоящих вагонов на ускорение грузов принимаем, что на каждом вагоне размещен один груз, который связан с ним упругой связью и трением. С целью сокращения числа решаемых уравнений в дальнейших исследованиях считаем, что тележки с рамой вагона имеют абсолютно жесткую связь. Тогда для любого числа участвующих в соударении вагонов математическая модель может быть представлена: |
