конспект лекций по математике для 38.08. Математика конспект лекций 1 курс спо. I. Числовые системы и приближенные вычисления Введение. Развитие понятия числа
 Скачать 1.06 Mb. Скачать 1.06 Mb.
|
ПредисловиеНастоящее пособие предназначено для студентов I курса любых специальностей в объеме 161 часа. Данный конспект содержит необходимый материал по десяти темам курса математики. изложение теоретического материала по всем темам сопровождается рассмотрением большого количества примеров и задач, ведется на доступном, по возможности строгом языке. Пособие может быть использовано студентами для самостоятельного изучения соответствующего материала, является базой для подготовки к экзаменам. кроме того, пособие может помочь студенту и в тех случаях, когда он что-то не успел записать на занятии, какие-то занятия были пропущены, в чем-то трудно (или нет времени) разобраться по другим пособиям, учебникам, когда некоторые вопросы «слишком длинны» в его конспектах или много фактического материала, который следует изучить за ограниченное количество времени. Автор надеется, что данное пособие будет способствовать более глубокому изучению материала студентами колледжа. Список обозначений:   – начало и конец решения примера, задачи – начало и конец решения примера, задачи   – начало и конец доказательства – начало и конец доказательства–  важные определения важные определения – обратите особое внимание – обратите особое вниманиеВ рамку заключены формулы, которые важно помнить. Домашние задания сдаются на проверку с соответствующей защитой по графику, который находится при кабинете математики. Консультации по математике проводятся по расписанию, находящемуся также в кабинете. ее глубокому изучению материала студентами колледжа.\мени., какие-то заняти Тема I. Числовые системы и приближенные вычисленияВведение. Развитие понятия числа. Мнимая единица. Комплексные числа. Действия над комплексными числами. Уравнения и неравенства с одной переменной. Уравнения, приводимые к квадратным. Системы двух линейных уравнений с двумя переменными. Системы трех линейных уравнений с тремя переменными. Системы нелинейных уравнений. Зачетное занятие по теме. Приложения: Домашнее задание № 1. Домашнее задание № 2. Контрольные (зачетные) вопросы по теме. Рубежный контроль (контрольная работа. Примерный вариант) Практическая работа № 1. Задания для самостоятельной работы. Литература. В результате изучения темы студенты должны знать: Числовые множества: натуральных, целых, рациональных, действительных, комплексных чисел; Формулы решения квадратного уравнения, разложения квадратного трехчлена на линейные множители; Правила составления и вычисления определителей второго и третьего порядков применительно к решению систем линейных уравнений; Применение метода интервалов к решению рациональных неравенств. В результате изучения темы студенты должны уметь: Выполнить с заданной точностью на инженерном или программируемом микрокалькуляторе (в режиме вычислений) арифметические действия; Вычислять значения элементарных функций; Выполнять действия над алгебраическими дробями; Решать уравнения с одной переменной первой и второй степени, биквадратных, иррациональных и др. Выполнять арифметические действия над комплексными числами в алгебраической форме; Решать квадратные уравнения с отрицательным дискриминантом; Решать линейные и квадратные неравенства с одной переменной, системы линейных неравенств; Решать системы линейных и нелинейных уравнений. Занятие 1.1 Введение. Развитие понятия числаРоль математики в подготовке специалистов среднего профессионального образования. Современная электронно-вычислительная техника и области ее применения. Понятие о математическом моделировании. Множество действительных чисел. Приближения действительных чисел конечными десятичными дробями. Числовая прямая. Промежутки. Окрестности точки. Простейшие вычисления с помощью МК. Формулы сокращенного умножения. Числа 1, 2, 3, 4, …… - множество натуральных чисел (N) Числа 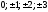 , ……. - множество целых чисел (Z) , ……. - множество целых чисел (Z)Числа 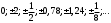 - множество рациональных чисел (Q) - множество рациональных чисел (Q)Любое рациональное число можно записать в виде дроби 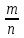 , где m , где m  Z , n Z , n  N N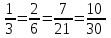 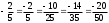 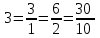 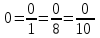 и т.д. и т.д.Разделив "m" на "n" получаем конечную или бесконечную десятичную дробь 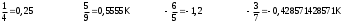  Как видим, у некоторых дробей десятичные знаки повторяются 0,5555 ……; 0,3333 ……; 4,5222 …….; Такие числа называются периодическими десятичными дробями и записываются: 4,959595 … = 4, (95) 2,125125125 … = 2, (125) 0,5121212 … = 0,5 (12) 2,13444 … = 2,13 (4) Каждая бесконечная периодическая дробь представляет собой рациональное число (докажем несколько позже), а пока будем использовать правило записи в виде обыкновенной дроби: 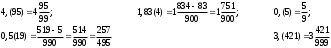 для чисто периодической дроби: в числителе пишется число, стоящее в периоде, а в знаменателе столько "9", сколько цифр в периоде, целая часть остается без изменения. для смешанной периодической дроби: в числителе разность между числом, стоящим после запятой, и числом, стоящим после запятой до периода, а в знаменателе столько "9", сколько цифр в периоде, со столькими "0", сколько цифр после запятой до периода Запишите в виде обыкновенной дроби: 5,21 (3) 13, (71) 14,72 (24) 0, (4) 0,7 (125) 10, (125) Числа, представляющие собой бесконечные непериодические десятичные дроби, называются иррациональными: 4,1728 …. 0,1078612 … 13,200941 … 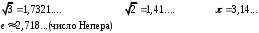 Теорема. Не существует рационального числа, квадрат которого равен числу 2 (предлагается самостоятельно рассмотреть доказательство (автор Яковлев "Алгебра и начала анализа" ч 1 п 8 (2)) Числа рациональные и иррациональные составляют множество действительных (вещественных) чисел (R). Действительные числа изображаются геометрически на прямой, которая называется осью действительных чисел -2,5 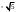 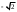 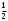 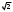 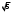 3,55 3,55 -3 -2 -1 0 1 2 3 4 Измеряется отрезок, соответствующий числу и откладывается на прямой.  Вы уже знакомы с числовыми множествами, называемыми промежутками. Перечислим их. Отрезок с концами а и b: [a;b] = 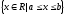 Интервал с концами a и b (a,b) = 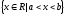 Полуоткрытые промежутки: (a,b] = 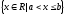 ; [a,b) = ; [a,b) = Число b - а называется длиной промежутка Бесконечные промежутки (лучи, полупрямые): 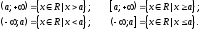 Числовая прямая: 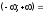 R RИ 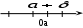 нтервал вида нтервал вида 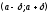 называют также называют также 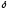 - окрестностью точки а - окрестностью точки аМ 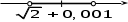 ожно сказать, например, что все десятичные приближения по недостатку и по избытку к числу ожно сказать, например, что все десятичные приближения по недостатку и по избытку к числу 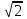 , начиная с третьего (т.е. приближения , начиная с третьего (т.е. приближения 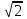 с точностью до 10 - n при n с точностью до 10 - n при n  3), попадают в 3), попадают в 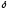 - окрестность точки - окрестность точки 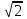 при при 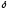 = 0,001. = 0,001.При выполнении действий над действительными числами используют правила округления числа 4,762  4,76 (с точностью до 0,01) 4,76 (с точностью до 0,01)4,762  4,8 (с точностью до 0,1) 4,8 (с точностью до 0,1)4,762  5 (с точностью до целых чисел) 5 (с точностью до целых чисел)Самостоятельная работа Действия на МК с учетом правила округления числа (простейшие вычисления) 2) 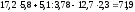 → →17.2  5.8 = x →П 5.8 = x →П5.1  3.78 = M + 3.78 = M +12.7  2.3 = M + MR 2.3 = M + MRКомбинированные действия на МК. 1) 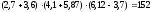 → →2.7 + 3.6 = x →П 4.1 + 5.87 = x MR → П 6.12-3.7 = x MR = Можно использовать скобки. 3) 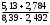 =1.342 ; 8.39 – 2.492 = X =1.342 ; 8.39 – 2.492 = X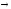 M ; 5.13 + 2.784 = M ; 5.13 + 2.784 =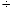 MR MR4) 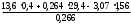 =32.0 13.6 · 0.4 = X =32.0 13.6 · 0.4 = X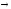 M; 0.264 · 29.4 =M+ M; 0.264 · 29.4 =M+3.07 · 1.56 = /–/ M+ MR 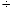 0,266 0,266Формулы сокращенного умножения 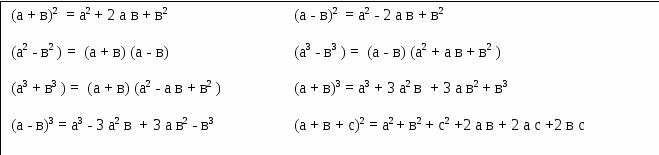 Выполнить действия (самостоятельно) 1. ( 4а + 3с )2 2. ( х3 - 2у + 3ху )2 3. ( 2х - 3у2 - х3у )2 4. ( х2 - 3у ) ( х2 + 3у ) 5. ( х + 2у ) (х2 - 2ху + 4у2 ) Контрольные вопросы Всякая ли обыкновенная дробь - число рациональное? Может ли быть рациональное число отрицательным? Почему бесконечную периодическую десятичную дробь считают рациональным числом? Назовите числа рациональные, иррациональные 2,75354276; 5, 3 (71); 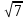 15,171 171 171 …; 4, 36 (5); 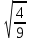 ; ; 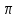 0, 36 78 ..; 1,276 ..; Какие числа, кроме рациональных и иррациональных являются действительными? Можно ли утверждать, что квадратный корень из любого натурального числа есть число иррациональное? Можно ли утверждать, что квадратный корень из любого нечетного числа есть число иррациональное? |
