конспект лекций по математике для 38.08. Математика конспект лекций 1 курс спо. I. Числовые системы и приближенные вычисления Введение. Развитие понятия числа
 Скачать 1.06 Mb. Скачать 1.06 Mb.
|
Контрольные зачетные вопросы по темеКакие числа называются рациональными? Какие числа называются иррациональными? Какие числа называются действительными? Геометрическое изображение действительных чисел. Правила записи десятичной периодической дроби в виде обыкновенной. Формулы сокращенного умножения. Формула решения квадратного уравнения (дискриминант, нахождение корней уравнения). Формула разложения квадратного трехчлена на множители. Решение биквадратных уравнений. Решение иррациональных уравнений. Решение неравенств с одной переменной. Метод интервалов. (его сущность) Мнимая единица, степень мнимой единицы. Что называется комплексным числом? Какие комплексные числа называются противоположными? сопряженными? Геометрическое изображение комплексных чисел. Модуль комплексного числа, его вычисление. Аргумент комплексного числа, его нахождение. Сложение и вычитание комплексных чисел. Умножение комплексных чисел в алгебраической форме. Разложение  на множители. на множители.Деление комплексных чисел в алгебраической форме. Определитель II порядка, его вычисление, свойства. Определитель III порядка, его вычисление, свойства. Правила нахождения определителей 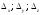 . .Правило Крамера при решении систем линейных уравнений. Приложение 4 Зачетная (контрольная) работа по теме IПримерный вариант1. Решить уравнения: 2. Решить неравенства:   3.Решить системы уравнений: 4. Выполнить действия:   Приложение 5 Практическая работа №1 «Решение уравнений, неравенств, систем уравнений» I Цель работы: Закрепление навыков решения уравнений и неравенств с одной переменной; систем линейных и нелинейных уравнений. II Наглядное пособие: МК, карточки заданий. III Теория. Действительные числа, их геометрическое изображение. Степень числа i Модуль и аргумент комплексного числа, их нахождение. Определитель второго порядка, его вычисление. Определитель третьего порядка, его вычисление. Свойства определителя. Метод интервалов, его применение. IV Практика (предлагаются задания по карточкам в четырёх вариантах, карточки прилагаются) V Контрольные вопросы 1) Как составить определители при переменных? 2) Сущность метода Гаусса, его применения. 3) Почему полученные корни при решении иррационального уравнения требуют проверки или предварительно указать ОДЗ и анализировать принадлежность полученных корней ОДЗ. 4) Какие корни имеет квадратное уравнение при D>0,D=0 и D<0 5) Применение методов интервала при n-ой кратности корней. 6) Укажите, какие из чисел есть числа иррациональные 1,4; 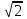 ; 1,5(2); ; 1,5(2); 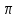 ; 2,(75); е; 11,96: ; 2,(75); е; 11,96:IV Литература Яковлев Г.Н. «Алгебра и начало анализа». Богомолов Н.В. « Практические занятия по математике». Справочник по математике(любого автора). Учебники 9-10-11 классов средней школы. Соловейчик И.Л., Лисичкин В.Т. « Математика» Вариант 1 Решить уравнения, неравенства, системы уравнения.   Вариант 2 Решить уравнения, неравенства, системы уравнения.  Вариант 3 Решить уравнения, неравенства, системы уравнения. 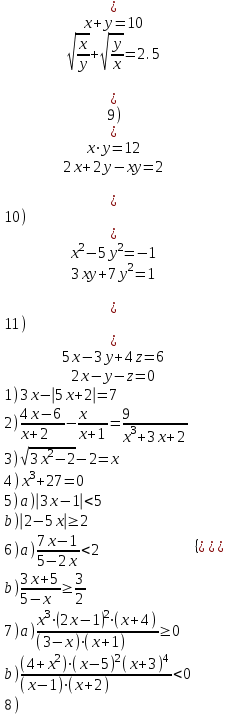 Вариант 4 Решить уравнения, неравенства, системы уравнения. 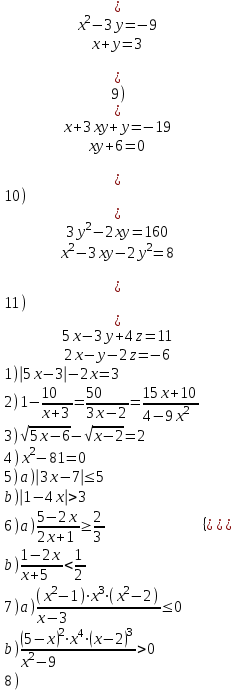 Приложение 6 Задания для самостоятельной работы1. Выполнить действия и результат изобразить геометрически. 1.1  1.2 1.2  2. Выполнить действия: 2.1 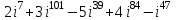 2.2 2.2 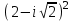 2.3 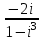 2.4 2.4 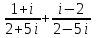 3. Найти модуль и аргумент комплексного числа. 3.1  3.2 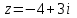 3.3 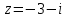 3.4  3.5 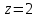 3.6 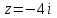 3.7  3.8  Уравнения с одной переменной. 4. Решить уравнения. 4.1  4.3 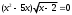 4.2  4.4  5. Решить биквадратное уравнение. 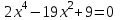 6. Решить уравнение методом введения новой переменной. 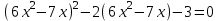 7. Сократить дробь:  и вычислить при х = – 2 и вычислить при х = – 28. Найти все корни уравнения: 8.1  8.2  8.3  8.4  8.5  9. Решить иррациональные уравнения. 9.1 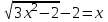 9.2 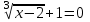 9.3  Неравенства I степени. 10. Решить неравенства: 10.1  10.2 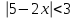 10.3  10.4  Неравенства II степени. 11. Решить неравенства: 11.1 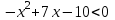 11.2  11.3  12. Решить системы неравенств: 12.1  12.2  12.3  13. Решить неравенство методом интервалов: 13.1  13.2 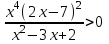 13.3  13.4 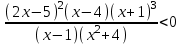 13.5 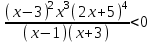 Системы уравнений. 14 Решить системы линейных уравнений: с двумя переменными (всеми способами) 14.1  с тремя переменными 14.2 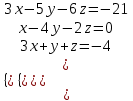 14.3 14.3 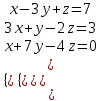 15. Решить системы нелинейных уравнений: 15.1 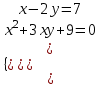 15.2 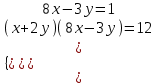 15.3  15.4 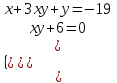 15.5  15.6  15.7  16. Вычислить при помощи МК 16.1 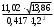 ; 16.2 ; 16.2 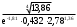 ; 16.3 ; 16.3  ; ; 16.4 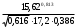 ; 16.5 ; 16.5  ; ; 16.6 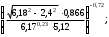 16.7 16.7 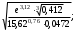 16.8 16.8  16.9  16.10 16.10 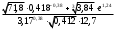 ЛитератураI Основная литература (О.Л.) 1. Яковлев Г. Н. ч. I «Алгебра и начала анализа» 2. Богомолов Н. В. «Практические занятия по математике» 3. Богомолов Н.В., Самойленко П.И. «Математика» 4. Дадаян А.А. «Математика» II Дополнительная литература (Д.Л.) М. Б. Балк, Г. Д. Галк, А. А. Полухин «Реальные применения мнимых чисел» Гусак Г. М. «Системы алгебраических уравнений» Сергиенко Л. Ю., Самойленко П. И. «Планирование учебного процесса по математике» Учебник «Алгебра и начала анализа» для 9 класса, для 10–11 классов III Методические и учебные пособия, изданные в НХК (М.П.) Калашникова В. А., Капустин Е. И. «Сборник материалов по математике для студентов I курса» Калашникова В. А. «Вычисления на инженерном МК» |
