конспект лекций по математике для 38.08. Математика конспект лекций 1 курс спо. I. Числовые системы и приближенные вычисления Введение. Развитие понятия числа
 Скачать 1.06 Mb. Скачать 1.06 Mb.
|
Занятие 1.4 Уравнения, приводимые к квадратнымБиквадратные уравнения Двучленные уравнения Иррациональные уравнения Вычисления на МК Биквадратное уравнение решается сведением к квадратному уравнению с помощью введения новой переменной. пусть решается сведением к квадратному уравнению с помощью введения новой переменной. пусть  , тогда имеем , тогда имеем 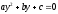 и решается квадратное уравнение относительно y. и решается квадратное уравнение относительно y.Например. 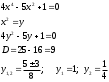 и тогда  , решаем эти уравнения: , решаем эти уравнения: получили четыре действительных корня. Ответ: получили четыре действительных корня. Ответ: 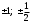 Решить самостоятельно: 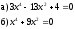 Двучленные уравнения:ные уравнения 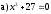 уравнение третьей степени и имеет 3 корня. Как их найти? Разложим левую часть уравнения на множители. уравнение третьей степени и имеет 3 корня. Как их найти? Разложим левую часть уравнения на множители. Применяем формулу:  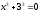  произведение равно нулю, если хотя бы один из сомножителей равен нулю, т.е. произведение равно нулю, если хотя бы один из сомножителей равен нулю, т.е.  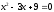  действительных корней нет, найдем мнимые действительных корней нет, найдем мнимые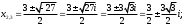 т.е. уравнение имеет один действительный корень т.е. уравнение имеет один действительный корень  и два мнимых и два мнимых   разложим на множители разложим на множители  имеем: имеем: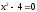 или или 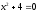   действительных корней нет, введём мнимую единицу действительных корней нет, введём мнимую единицу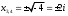 есть два мнимых корня есть два мнимых корняОтвет: 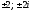 . .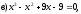 группируем члены группируем члены выносим общий множитель из каждой скобки выносим общий множитель из каждой скобки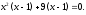 Вынесем 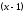 за скобки за скобки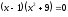 и тогда и тогда или или 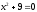 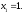 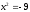 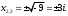 Ответ: Ответ:  . .Самостоятельно: 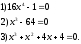 Иррациональные уравнения Уравнения, содержащие переменную под знаком корня, называются иррациональными. При решении иррациональных уравнений необходимо учитывать: При извлечении корня четной степени берется только арифметическое его значение При возведении выражения, содержащего переменную, в степень может быть нарушена равносильность выражений Рассмотрим на примерах:  перенесем x в правую часть  возведем обе части уравнения в квадрат. Так как  , то получаем , то получаем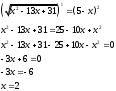 так как при решении уравнения мы возводили в квадрат, то корень  требует проверки. Итак требует проверки. Итак  подставляем в данное уравнение подставляем в данное уравнение 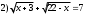 уравнение содержит два корня, перенесем один из корней в правую часть  возведем обе части уравнения в квадрат 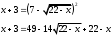 остался один корень. Перенесем его в левую часть, остальные члены – в правую 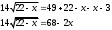 сократим обе части на 2 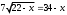 и опять возведем в квадрат обе части уравнения: 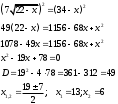 Проверка  Ответ: x = 13; x = 6. М 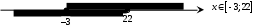 ожно было указать сразу ОДЗ и получив корни, сравнить с ОДЗ ожно было указать сразу ОДЗ и получив корни, сравнить с ОДЗ полученные корни x = 13 и x = 6 удовлетворяют ОДЗ  и следовательно и следовательно Ответ: x = 13; x = 6 3)  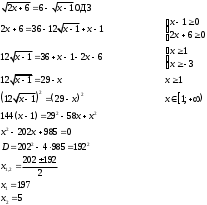 Из того, что 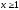 делаем вывод, что делаем вывод, что 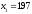 и и  являются корнями уравнения. Однако проверка показывает, что являются корнями уравнения. Однако проверка показывает, что 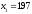 в данном случае является посторонним корнем в данном случае является посторонним корнем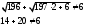  Ответ: 5. Ответ: 5.Решить самостоятельно: 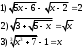 Решим уравнения:  Отсюда 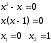 и и  Проверим корни:  Ответ: 0; 1; 2. 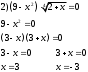 или или 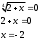 ОДЗ: ОДЗ:  Проверяя полученные корни, видим, что 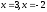 удовлетворяют ОДЗ, а вот удовлетворяют ОДЗ, а вот 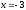 – посторонний корень. Ответ: – посторонний корень. Ответ: 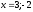 . .Вычислить на МК Проверить результаты: 1)  = 0,0441 2) = 0,0441 2) 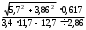 = 0.120 = 0.1203) 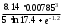 = 2.7 = 2.7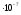 4) 4) 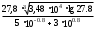 = 52.02 = 52.025)  = 6.65 = 6.65 |
