конспект лекций по математике для 38.08. Математика конспект лекций 1 курс спо. I. Числовые системы и приближенные вычисления Введение. Развитие понятия числа
 Скачать 1.06 Mb. Скачать 1.06 Mb.
|
Занятие 1.5 Системы двух линейных уравнений с двумя переменными. Определитель второго порядка, его свойства. Правило Крамера при решении систем уравнений.Вычисления с помощью МКСистемы двух линейных уравнений с двумя переменными Определитель второго порядка, его вычисление Правило Крамера при решении систем уравнений Свойства определителя второго порядка Вычисления при помощи МК. Система двух линейных уравнений с двумя переменнымив общем виде имеет вид  Решением системы уравнений называется упорядоченная пара чисел, удовлетворяющая каждому уравнению этой системы. При решении такой системы могут быть использованы известные методы: 1) подстановки; 2) алгебраического сложения; 3) графически. Но существует ещё метод решения, который особенно удобен в том случае, когда коэффициенты  отличны от единицы или содержат буквенные выражения. отличны от единицы или содержат буквенные выражения. Имеем систему уравнений  Число 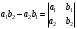 называется определителем второго порядка. Вертикальные прямые – знак определителя. Обозначается определитель знаком называется определителем второго порядка. Вертикальные прямые – знак определителя. Обозначается определитель знаком 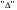 (дельта). (дельта).Итак определитель – это число, которое вычисляется по определенному правилу   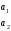 – первый столбик (коэффициенты при переменной x) – первый столбик (коэффициенты при переменной x) – второй столбик (коэффициенты при переменной y) – второй столбик (коэффициенты при переменной y)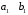 – первая строчка (коэффициенты при переменных первого уравнения) – первая строчка (коэффициенты при переменных первого уравнения)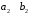 – вторая строчка (коэффициенты при переменных второго уравнения) – вторая строчка (коэффициенты при переменных второго уравнения)Определители при переменных  и и  получаются из определителя системы путем замены соответствующего столбика столбиком из свободных членов. получаются из определителя системы путем замены соответствующего столбика столбиком из свободных членов. Для нахождения значений переменных x и y используются формулы 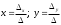 , которые называются формулами Крамера. , которые называются формулами Крамера.Исследуем Если 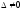 – система имеет единственное решение – система имеет единственное решениеЕсли Если  сли ема не имеет решенияое решениера.ся из определителя системы путем замены соответствующего столбика столбиком из свободных чи сли ема не имеет решенияое решениера.ся из определителя системы путем замены соответствующего столбика столбиком из свободных чи 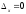 и и 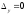 – система имеет множество решений. – система имеет множество решений.Например 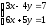   Ответ: (1; –1). Ответ: (1; –1).Основные свойства определителяОпределитель не изменится, если его строки заменить столбцами, и наоборот  При перестановке двух столбцов (строчек) определитель меняет свой знак на противоположный. Определитель, имеющий два одинаковых или пропорциональных столбца (строчки) равен нулю. Общий множитель столбца (строчки) определителя можно вынести за знак определителя. Рассмотрим примеры: Решить систему уравнений:  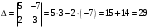  система имеет единственное решение система имеет единственное решение Ответ: (1; –2). Ответ: (1; –2).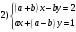 Более рационально систему решить через определитель второго порядка 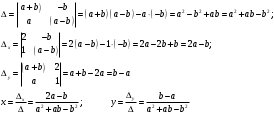 Система имеет единственное решение при условии, что  т.е. т.е. 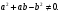 При решении системы двух линейных уравнений с двумя переменными следует помнить, что решение можно выполнить любым из известных методов решения, просто следует выбрать каким методом более рационально для данной системы. 3)  Решим систему всеми способами, т.е. убедимся, что результат получается одинаковый и определимся, какой из методов более рационально применим для данной системы. 1) Способ подстановки. 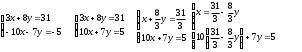 Решаем второе уравнение относительно «y»: 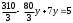 , приведем к общему знаменателю и так как , приведем к общему знаменателю и так как  , то , то  Ответ: x = –3; y = 5. Ответ: x = –3; y = 5.2) Способ алгебраического сложения у 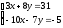 равняем по модулю коэффициенты при x, для этого умножим первое уравнение на 10, а второе – на 3. равняем по модулю коэффициенты при x, для этого умножим первое уравнение на 10, а второе – на 3.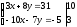  почленно сложим почленно сложим подставим y = 5 в любое из уравнений системы, например в первое, и найдем x  получаем x = –3; y = 5, как и в первом случае. 3) графически (следует помнить, что результаты могут быть получены приближенно, что можно объяснить нашим зрением, умением проводить линии, выбором масштаба, неудобством записи числа и т.д.) г  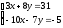 рафиком каждого уравнения является прямая, а прямая определяется двумя точками. рафиком каждого уравнения является прямая, а прямая определяется двумя точками.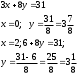  (–3; 5) 4) C помощью определителя:  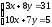 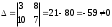 единственное решение единственное решение Ответ: (–3; 5). Каким же способом более рационально можно было решить эту систему? Вы правы, конечно с помощью определителя. Самостоятельно (любым способом)  Контрольные вопросы. Что называется определителем II порядка? Как вычисляется определитель II порядка? Какими свойствами обладает определитель? При каких значениях a система 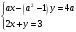 имеет решение, для которого x = 4. имеет решение, для которого x = 4.Вычислить при помощи МК. 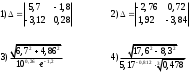 |
