конспект лекций по математике для 38.08. Математика конспект лекций 1 курс спо. I. Числовые системы и приближенные вычисления Введение. Развитие понятия числа
 Скачать 1.06 Mb. Скачать 1.06 Mb.
|
Занятие 1.7 Системы нелинейных уравненийПонятие системы нелинейных уравнений. Решение систем нелинейных уравнений. Вычисления при помощи МК. Система уравнений, в которой хотя бы одно из уравнений содержит переменную во второй или выше степени называется нелинейной системой уравнений. Решить систему – значит найти все ее решения. Решением системы называется пара чисел, удовлетворяющая каждому из уравнений системы. Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения. Система называется определенной, если она имеет конечное число решений, и неопределенной, если она имеет бесконечное множество решений. Две системы называются равносильными, если они имеют одно и то же множество решений. При решении систем нелинейных уравнений наиболее широко используются методы: 1. подстановки; 2. алгебраического сложения; 3. графический; 4. искусственные приемы (применение формул сокращенного умножения, введения новой переменной, использование теоремы Виета и т.д.). Рассмотрим примеры решения систем уравнений. 1. Решить способом подстановки. 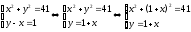 первое уравнение содержит одну переменную, можно выписать это уравнение и решить его. 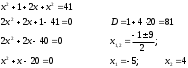 и тогда, подставив полученные значения  и и 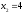 во второе уравнение, получаем во второе уравнение, получаем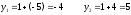 Получаем две пары чисел 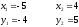 , которые являются решением данной системы уравнений. Ответ: (5; –4); (4; 5). , которые являются решением данной системы уравнений. Ответ: (5; –4); (4; 5).2. Решить способом алгебраического сложения  Видим, что каждое из уравнений содержит  , сложим почленно и получаем уравнение относительно одной переменной. , сложим почленно и получаем уравнение относительно одной переменной.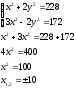 И тогда имеем 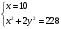 и и 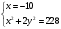 , т.к. системы содержат только , т.к. системы содержат только  , а , а  , то можно решить только одну из систем и получить значения y , то можно решить только одну из систем и получить значения y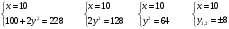 И 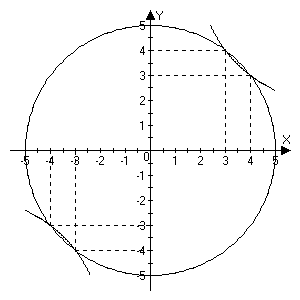 тогда решением системы будут тогда решением системы будут 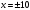 и и  . .3. Решить графически 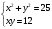 Графическое решение системы уравнений с двумя переменными сводится к отысканию координат общих точек графиков уравнений: 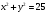 – окружность с центром (0; 0) и R = 5 – окружность с центром (0; 0) и R = 5 – гипербола – гипербола
Имеем пары чисел (3; 4); (4; 3); (–3; –4); (–4; –3) которые определяют координаты четырех точек. 4. Решить систему уравнений введением новой переменной. л 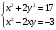 евая часть каждого из уравнений системы есть однородный (одинаковой степени) многочлен относительно переменных x и y. евая часть каждого из уравнений системы есть однородный (одинаковой степени) многочлен относительно переменных x и y.Пусть y = xt   , т.к. тогда и , т.к. тогда и  , что невозможно. , что невозможно.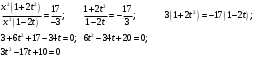 Решаем уравнение относительно t  Теперь можно записать системы уравнений  и и  Решаем способом подстановки первую систему: 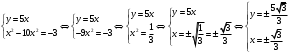 Аналогично решение второй системы: 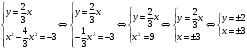 Таким образом получаем пары чисел:  4.  Пусть 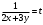 и и 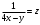 , тогда имеем систему уравнений , тогда имеем систему уравнений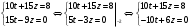 Применим способ алгебраического сложения  , тогда , тогда 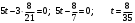 Следовательно имеем систему уравнений  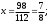 подставив значение подставив значение  в любое из уравнений системы в любое из уравнений системы  т.е. решением системы является пара чисел т.е. решением системы является пара чисел 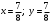 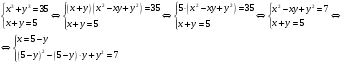 Решаем второе уравнение относительно y; 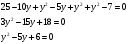 по теореме Виета имеем по теореме Виета имеем  , , тогда  , т.е. решением системы будут пары чисел , т.е. решением системы будут пары чисел  и и 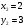 6 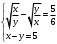 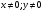 упростим первое уравнение системы с помощью введения новой переменной упростим первое уравнение системы с помощью введения новой переменнойПусть  , тогда , тогда  и уравнение имеет вид и уравнение имеет вид 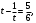 т.к. т.к.  то то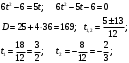 и тогда имеем системы 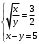 и и 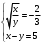 Решаем эти системы относительно x и y  Ответ: (9; 4); (–4; –9). Замечание. При решении систем нелинейных уравнений предварительно надо решить, каким методом может быть решена система, какие надо выполнить преобразования, какие операции приводят к упрощению систем. Самостоятельно: 1)  3) 3)  2) 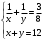 4) 4) 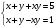 Вычислить при помощи МК. |
