конспект лекций по математике для 38.08. Математика конспект лекций 1 курс спо. I. Числовые системы и приближенные вычисления Введение. Развитие понятия числа
 Скачать 1.06 Mb. Скачать 1.06 Mb.
|
Занятие 1.6 Системы трех линейных уравнений с тремя переменными. Определитель III порядкаОбщий вид системы трех линейных уравнений с тремя переменными. Определитель III порядка. Вычисление определителя III порядка. Решение системы трех линейных уравнений с тремя переменными. Правило Крамера. Вычисления при помощи МК. Система трех линейных уравнений с тремя переменными имеет вид: 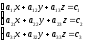 На I курсе рассматривается решение такой системы с помощью определителя третьего порядка. Выражение, составленное из коэффициентов при переменных в виде таблицы 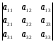 называется определителем третьего поряда. называется определителем третьего поряда.Определитель третьего порядка вычислить можно через определитель второго порядка или по правилу Саррюса (правило треугольника). Через определитель II порядка. 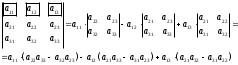 Выделяем 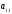 и мысленно вычеркиваем по столбику и строчке, оставшиеся члены составляют определитель второго порядка. Берем и мысленно вычеркиваем по столбику и строчке, оставшиеся члены составляют определитель второго порядка. Берем 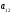 с противоположным знаком и вычеркиваем первую строчку и второй столбик, оставшиеся члены составляют определитель II порядка. Аналогично берем с противоположным знаком и вычеркиваем первую строчку и второй столбик, оставшиеся члены составляют определитель II порядка. Аналогично берем 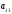 и вычеркиваем первую строчку и третий столбик, оставшиеся члены составляют определитель II порядка. и вычеркиваем первую строчку и третий столбик, оставшиеся члены составляют определитель II порядка.Выполняем вычисления определителей II порядка по известному уже нам правилу. Например: 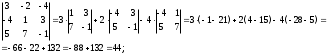 Правило треугольника (Саррюса). Рассмотрим схематически a 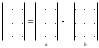 ) (основания равнобедренных треугольников параллельны главной диагонали) ) (основания равнобедренных треугольников параллельны главной диагонали)b) (основания равнобедренных треугольников параллельны побочной диагонали) Пример: (возьмем тот же определитель)  В дальнейшем запись будем вести так  Определители 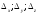 получаются из определителя системы путем замены соответствующего столбика столбиком из свободных членов и вычисляются по тому же правилу, что и определитель системы. получаются из определителя системы путем замены соответствующего столбика столбиком из свободных членов и вычисляются по тому же правилу, что и определитель системы.Для нахождения значений 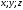 пользуются правилами Крамера пользуются правилами Крамера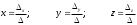 Исследование: Если 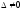 , то система имеет единственное решение , то система имеет единственное решениеЕсли  , то система несовместима, т.е. не имеет решения , то система несовместима, т.е. не имеет решения (либо  либо либо 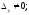 либо либо 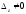 ) )Если  , то система неопределенна, т.е. имеет множество решений , то система неопределенна, т.е. имеет множество решений( 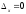 и и 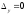 и и 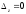 ) )Определитель III порядка обладает всеми свойствами определителя II порядка. Например, решить систему уравнений 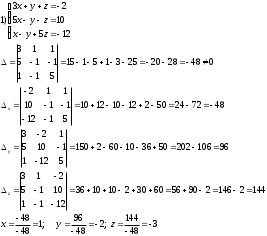 Ответ: (1; –2; –3). 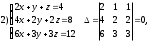 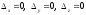 , , так как коэффициенты при переменных и свободные члены пропорциональны.  Система имеет множество решений, т.е. неопределена.   и и 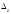 можно уже не находить. Следовательно система не имеет решения. можно уже не находить. Следовательно система не имеет решения.Самостоятельно: 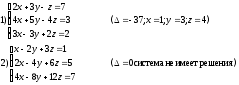 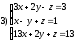 ( 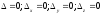 система имеет множество решений) система имеет множество решений)Контрольные вопросы: Общий вид системы трех линейных уравнений с тремя переменными. Что называется определителем III порядка? Правила вычисления определителя III порядка (через определитель II порядка, правило треугольника). Свойства определителя III порядка. Формулы (правила) Крамера. Вычислить при помощи МК: 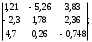 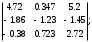  |
