Механіка. I. механiка кінематика основнi формули

• Название: I. механiка кінематика основнi формули
• Анкор: Механіка
• Дата: 03.11.2020
• Размер: 1.75 Mb.
• Имя файла: I._MEHANIKA.doc
• Тип: Документы; #147829
• страница: 8 из 10

Основні формули

1. Закон збереження моменту імпульсу системи тіл, що обер­та­ються навколо нерухомої осі :

,

де – момент інерцій системи тіл відносно осі ; – кутова швидкість обертання тіл системи навколо осі .

2. Кінетична енергія тіла, що обертається навколо нерухомої осі ,

,

де – проекція на вісь мо­менту імпульсу.

Приклад розв'язання задачі

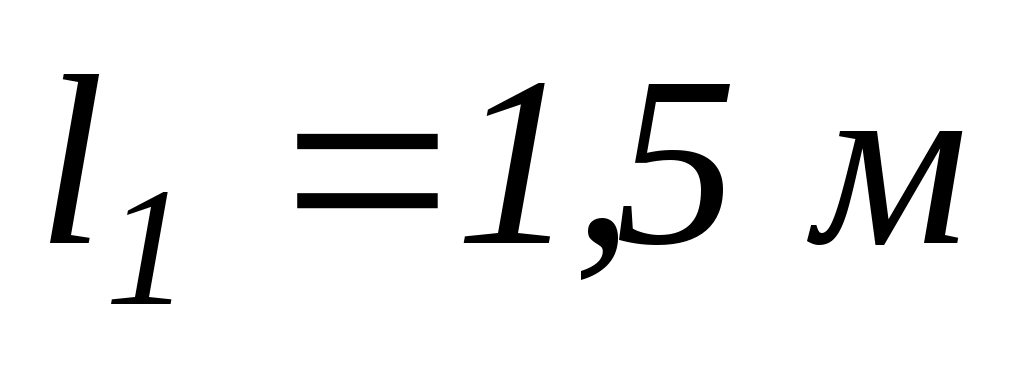
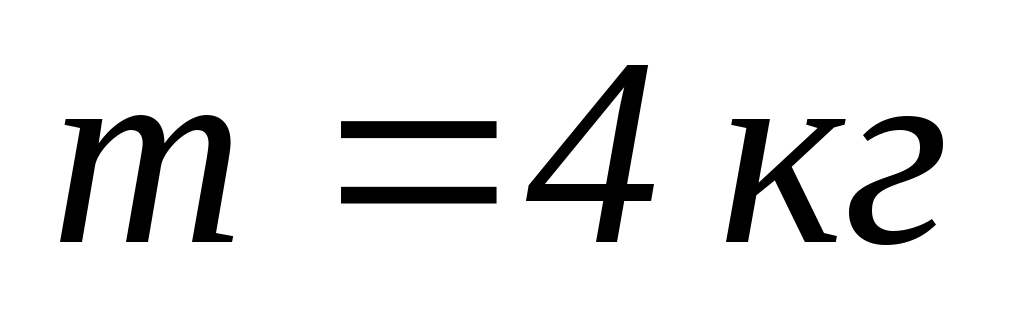
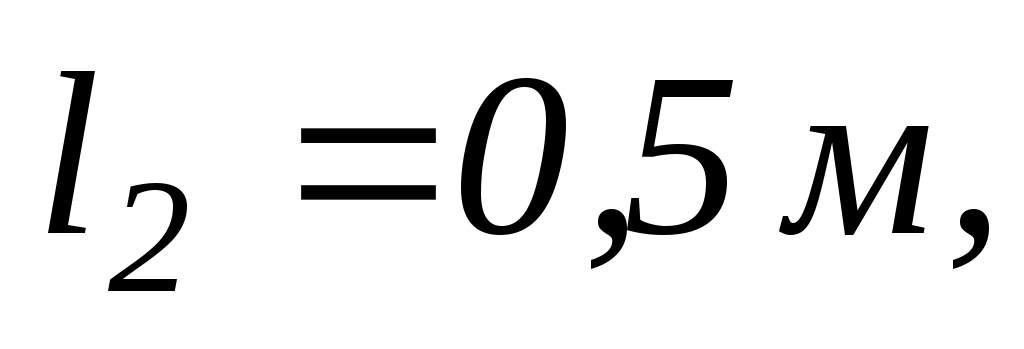
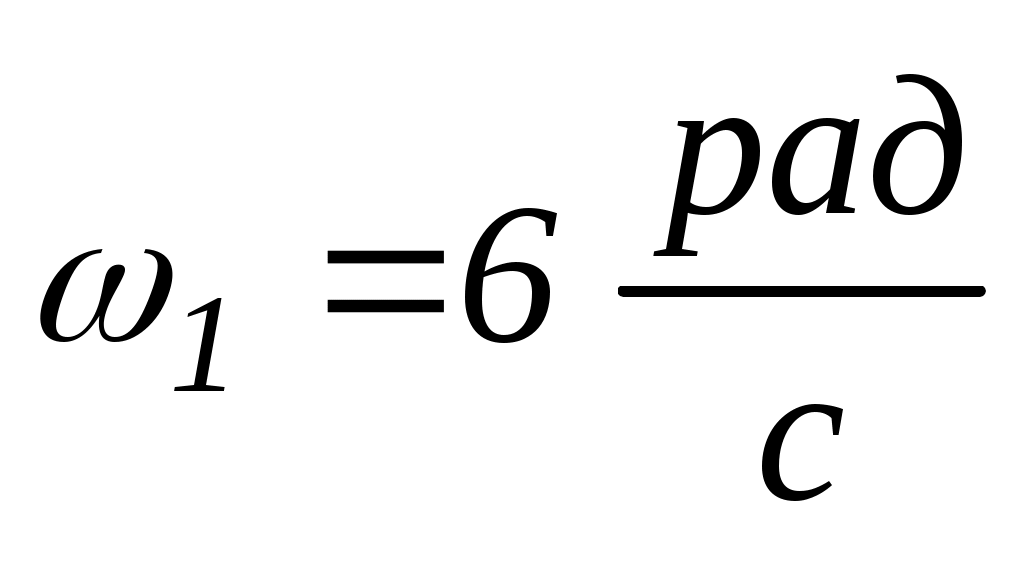
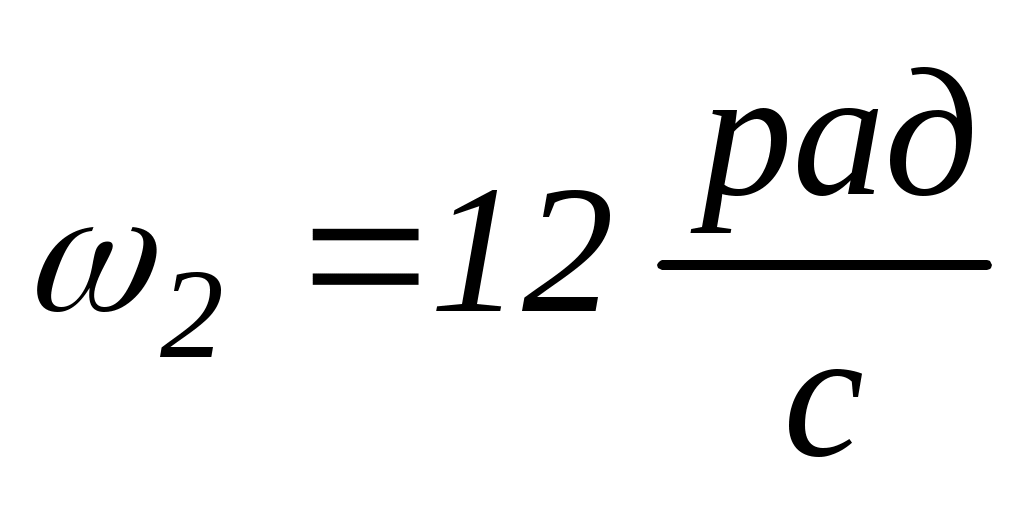
На легкому столику, який обертається, стоїть людина і три­має на випростаних руках на відстані одна від одної, гирі масою кожна. По­тім людина зближує гирі до від­стані при цьому кутова швидкість обертання столика зростає від до . Визначити момент інерцій тіла людини відносно осі обертання.

Розв’язання

Людина, що тримає гирі й обертається на столику, являє со­бою, разом зі столиком, замкнену систему. Момент імпульсу сис­теми повинен мати стале зна­чення .

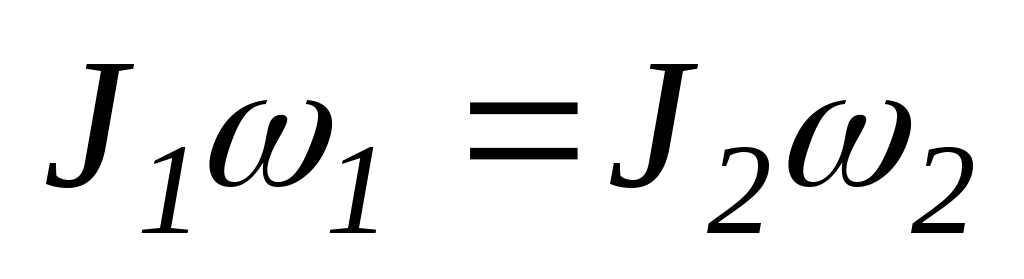
Момент інерцій системи, яка розглядається в даній задачі, до­рівнює сумі моменту інерцій тіла людини відносно осі обер­тання і моменту інерцій гир в ру­ках людини:

, .

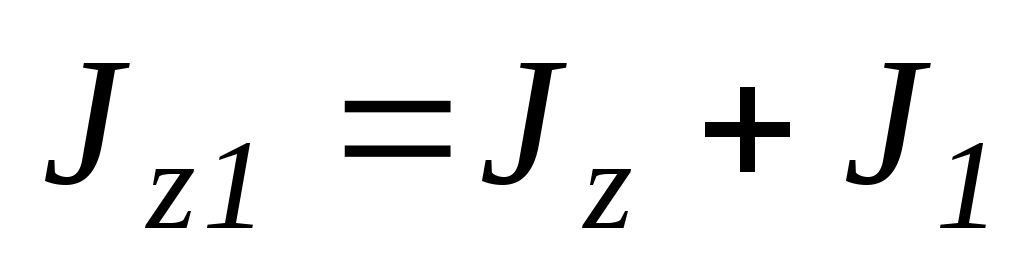
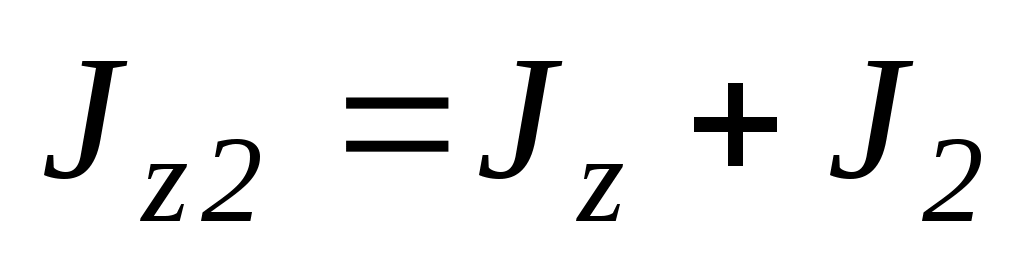
Вважаючи гирі наближено як точкові тіла, маємо

, ,

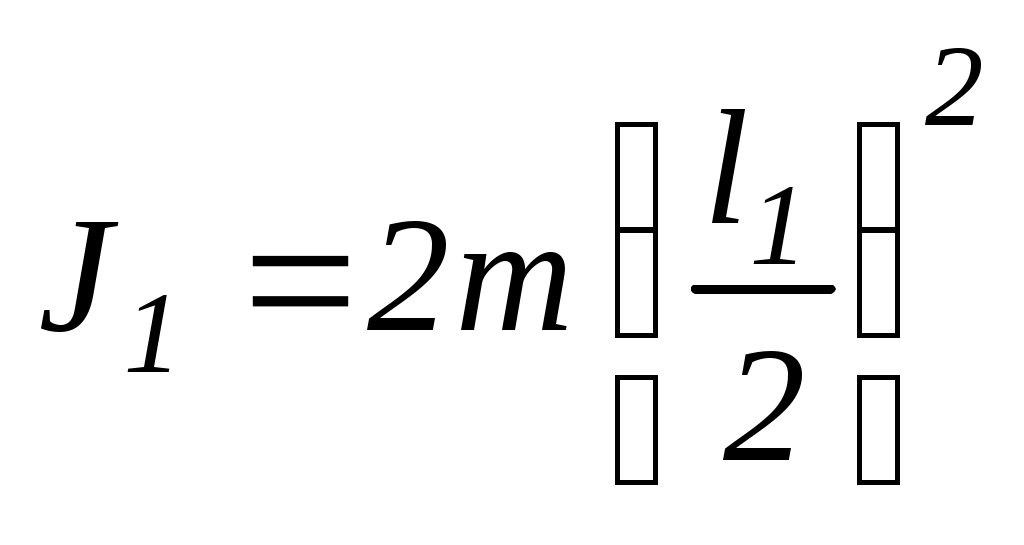
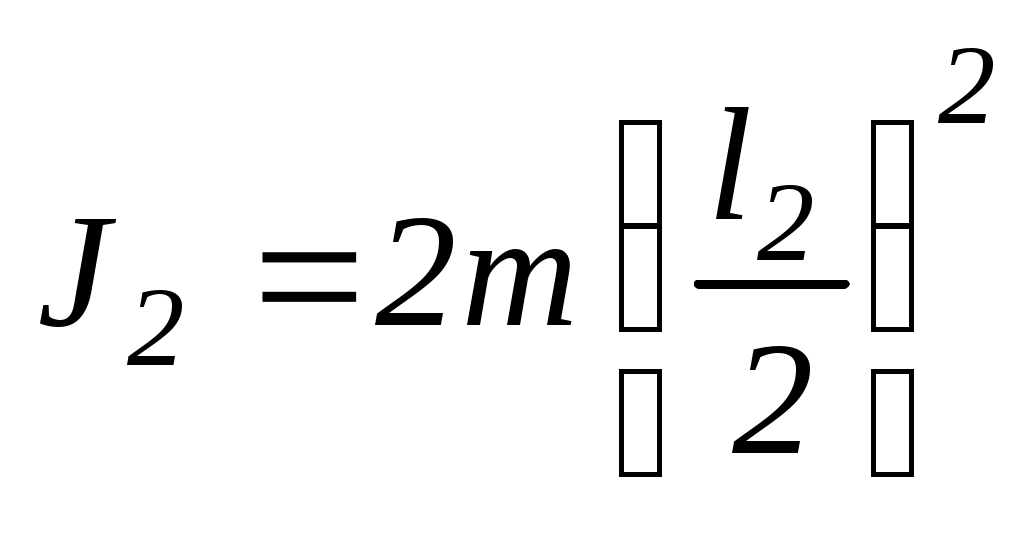
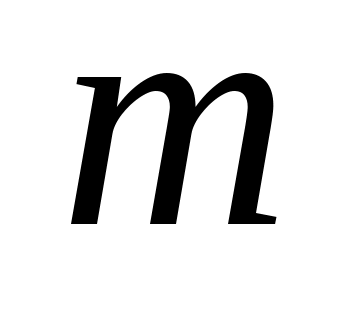
де – маса кожної з гир.

Отже,





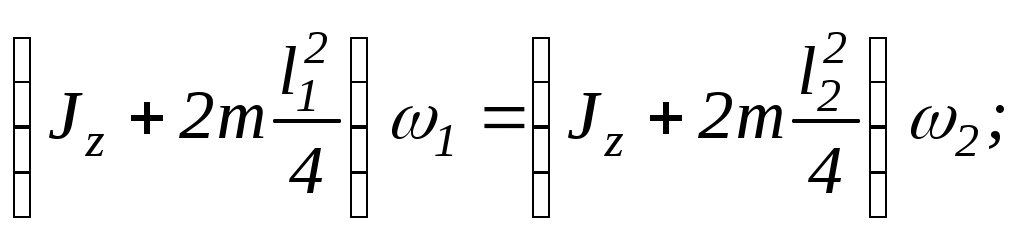
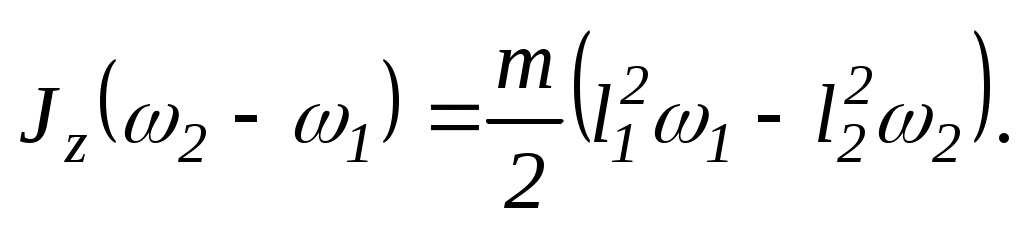
звідси



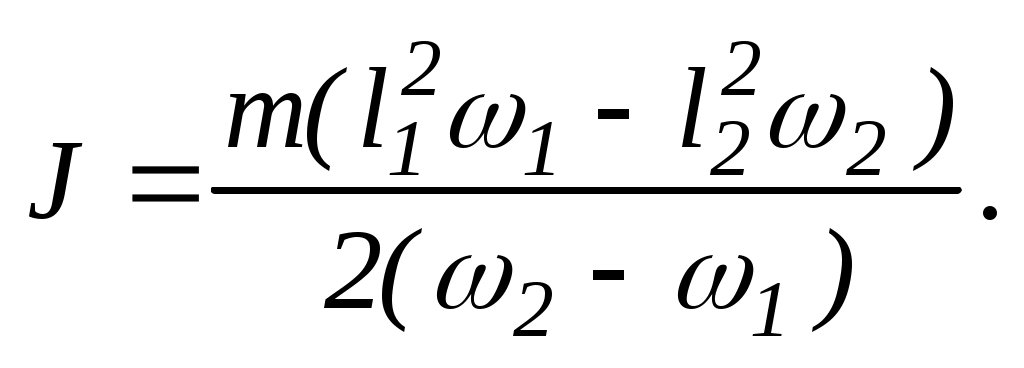
Підставимо числові значення і проведемо розрахунки:

.

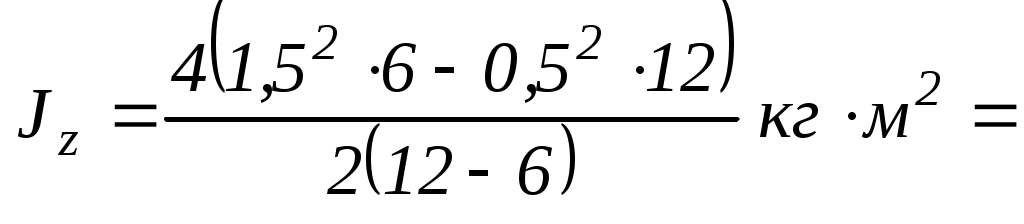
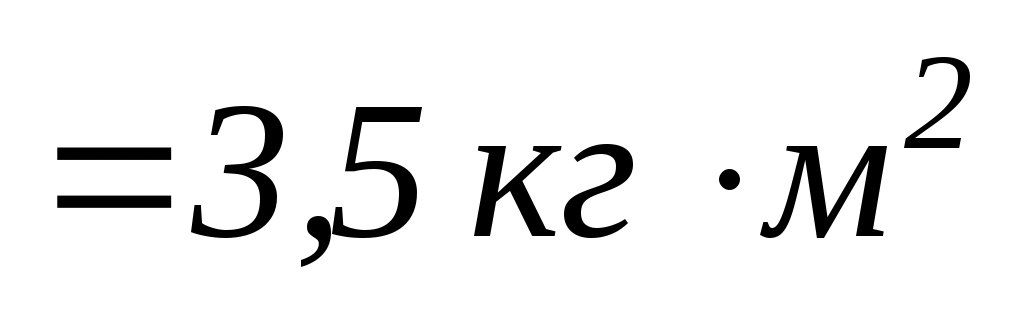
Задачі контрольної роботи

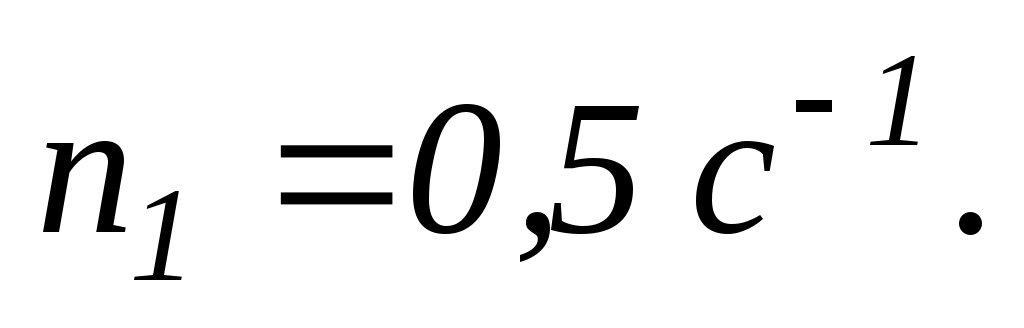
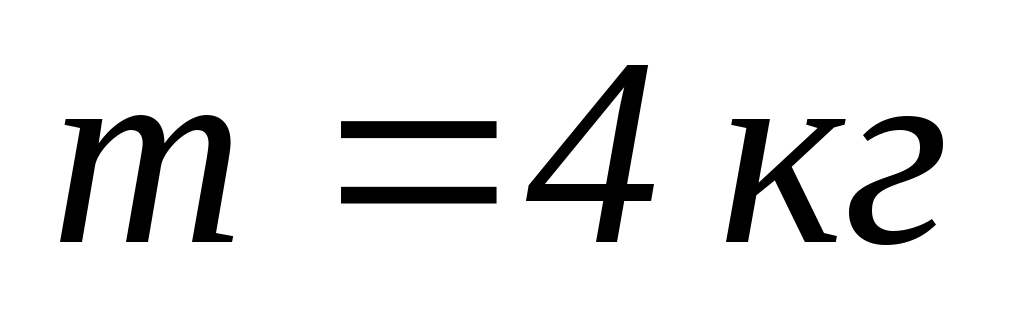
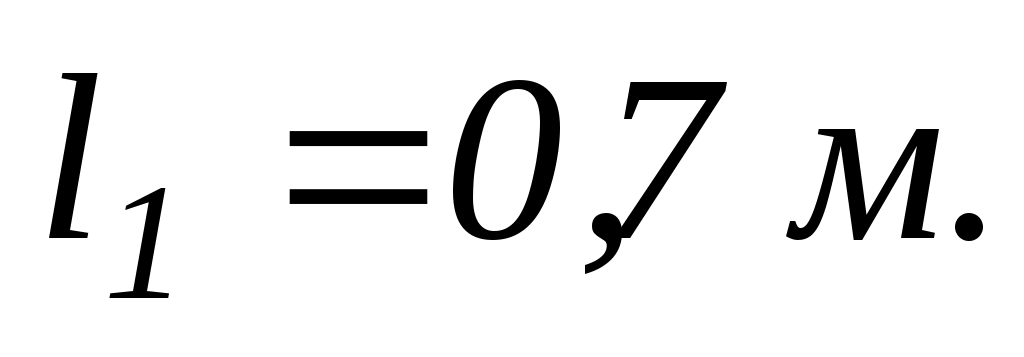
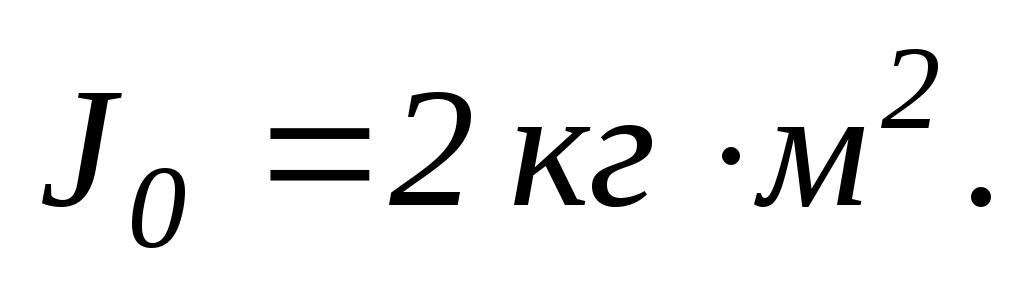
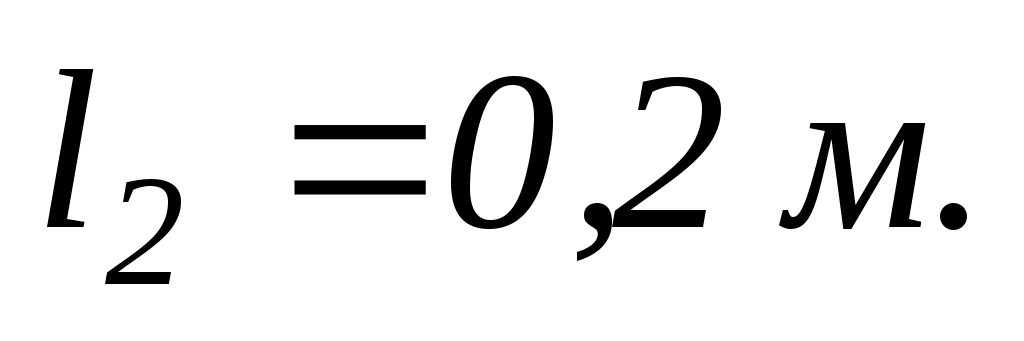
7.1. Людина сидить в центрі лави Жуковського, що обертається за інерцією навколо нерухомої вертикальної осі з частотою У витягнутих в сторони руках вона тримає по гирі масою кожна. Відстань від кожної гирі до осі обертання Сумарний момент інерції тіла людини і лави відносно осі обертання Людина притискає гирі до себе так, що відстань від кожної гирі до осі стане Визначити роботу яку виконає людина.

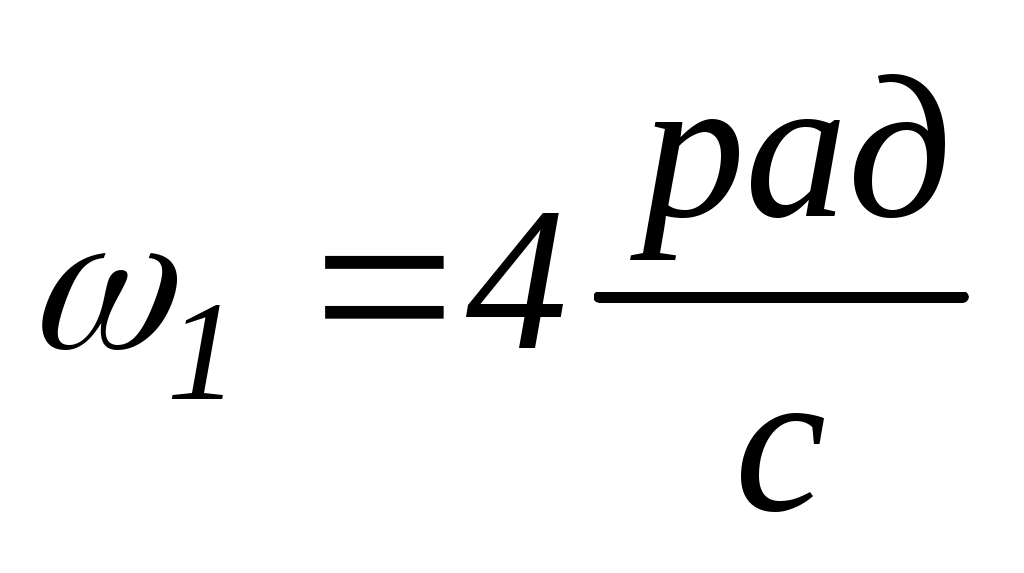
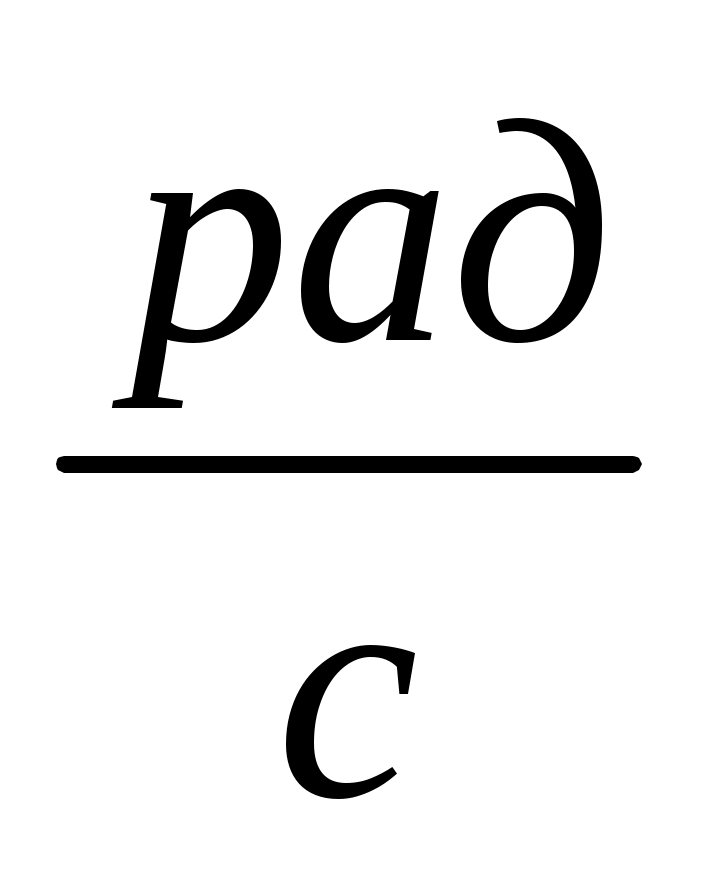
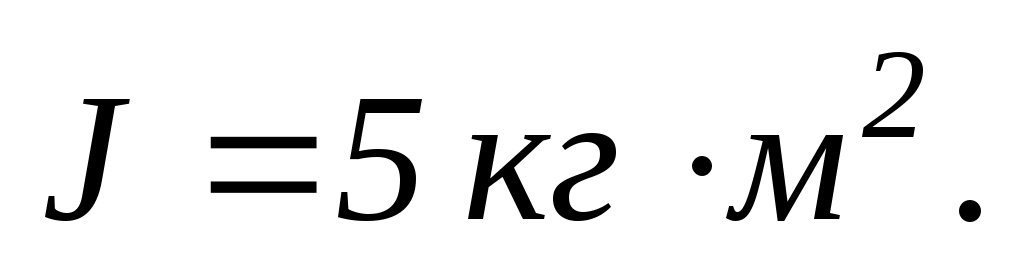
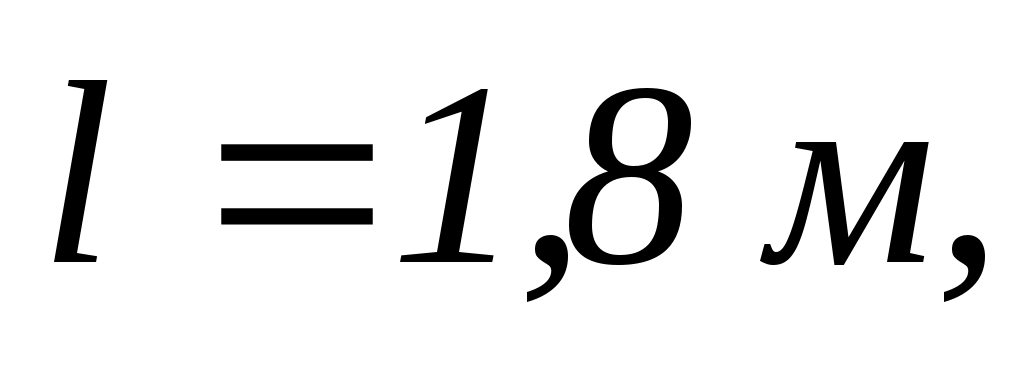
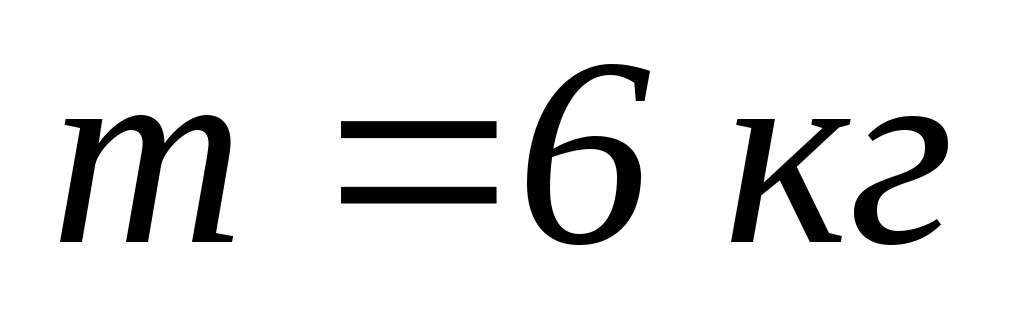
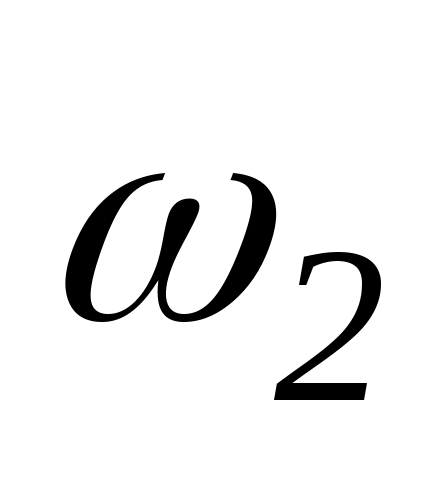
7.2. На лаві Жуковського стоїть людина і тримає в руках стрижень вертикально по осі лави. Лава з людиною обертається з кутовою швидкістю . Сумарний момент інерцій людини і лави Довжина стрижня маса . Вважати, що центр мас стрижня з людиною знаходиться на осі платформи. З якою швидкістю буде обертатися лава з людиною, якщо повернути стри­жень так, щоб він зайняв горизонтальне положення?

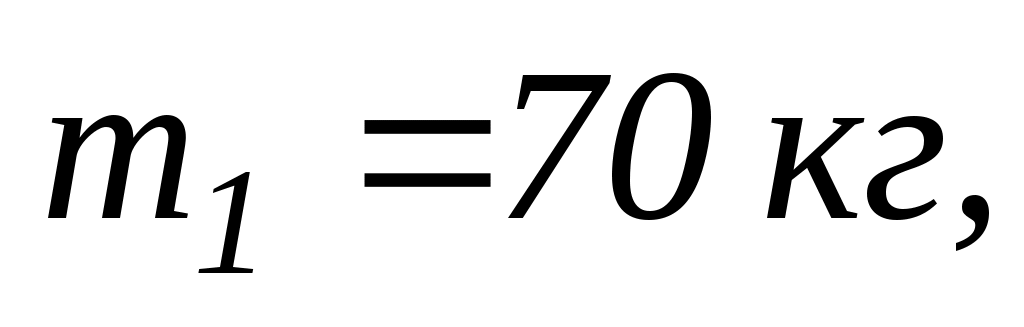
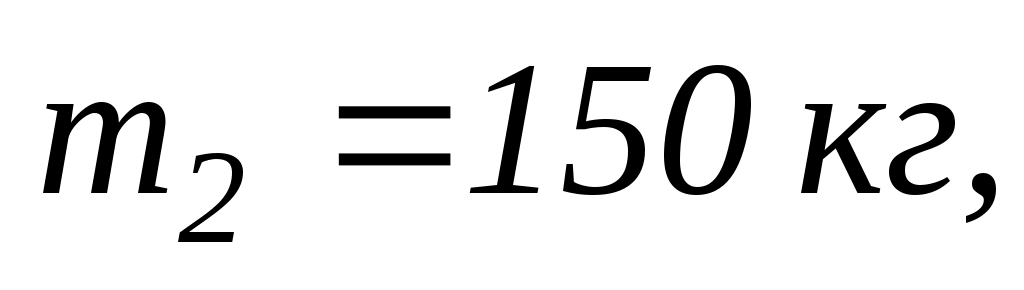
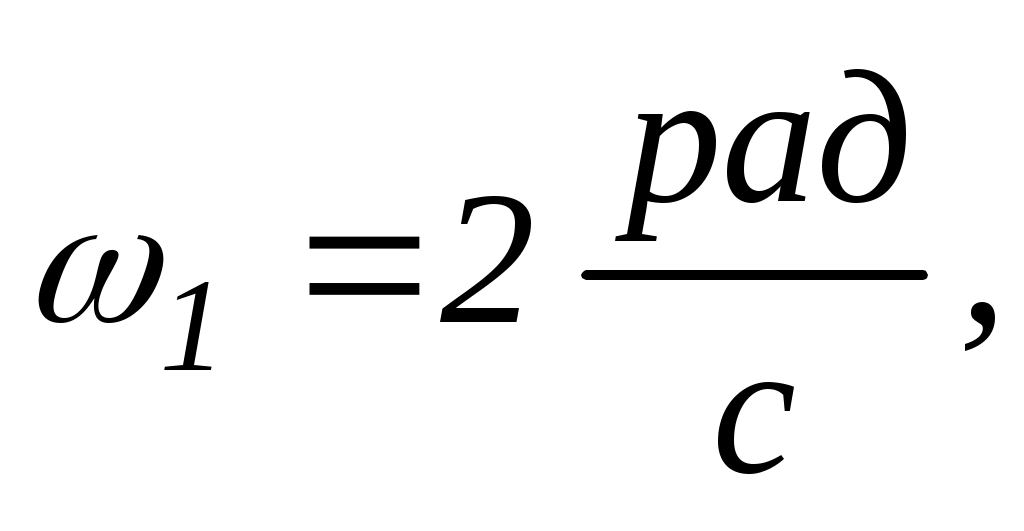
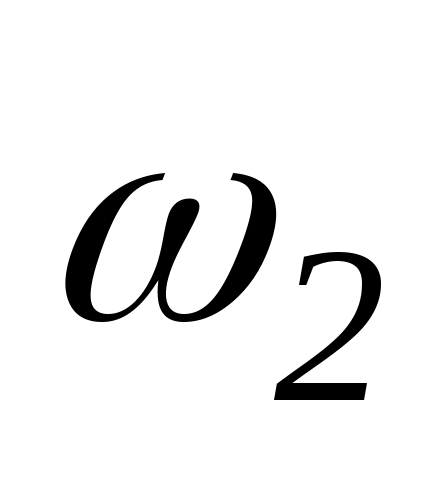
7.3. Людина масою що стоїть на краю горизонтальної платформи масою що обертається за інерцією навколо нерухомої вертикальної осі з кутовою швидкістю переходить до центра платформи. Вважаючи платформу круглим однорідним диском, а людину точковою масою, визначити, з якою частотою буде тоді обертатися платформа?

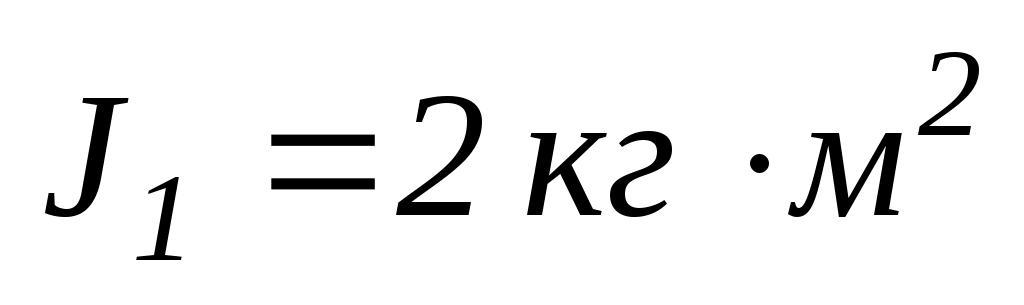
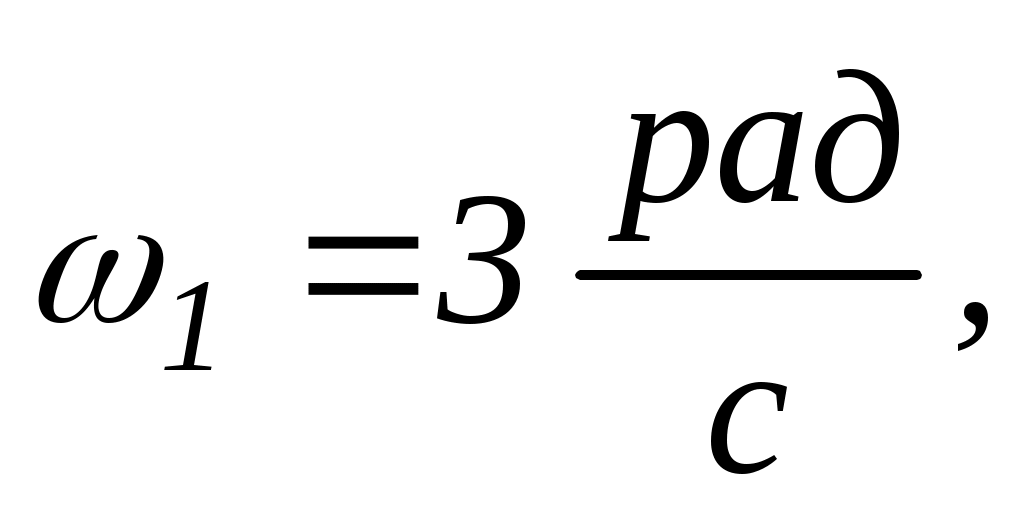
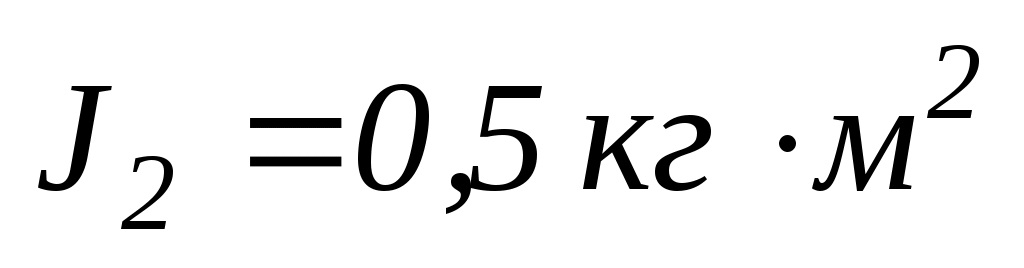
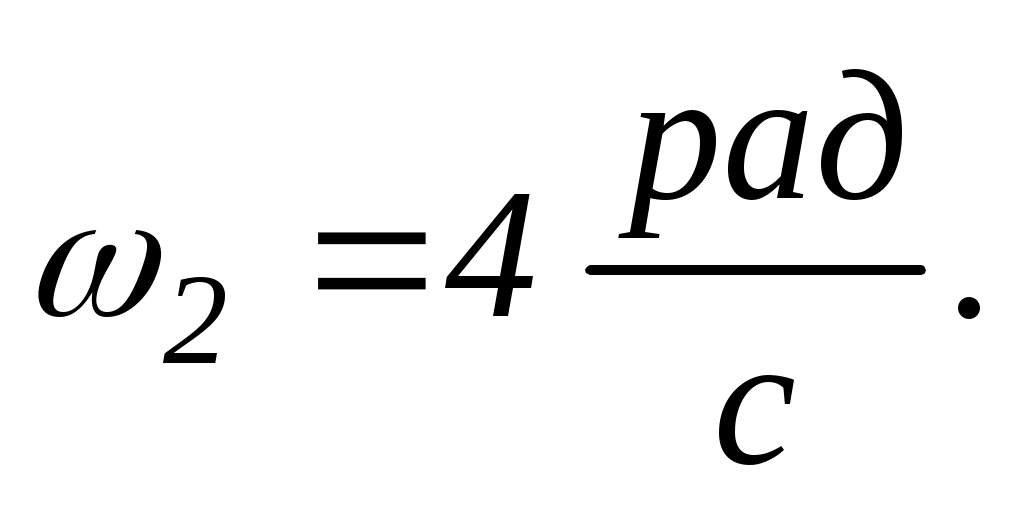
7.4. Два гумові диски з шорсткими поверхнями обертаються навко­ло осей, що лежать на одній вертикалі, причому площини дисків пара­лельні. Перший диск має момент інерцій і кутову швид­кість другий – і Верхній диск падає на нижній і з’єднується з ним. Знайти кутову швидкість дисків.

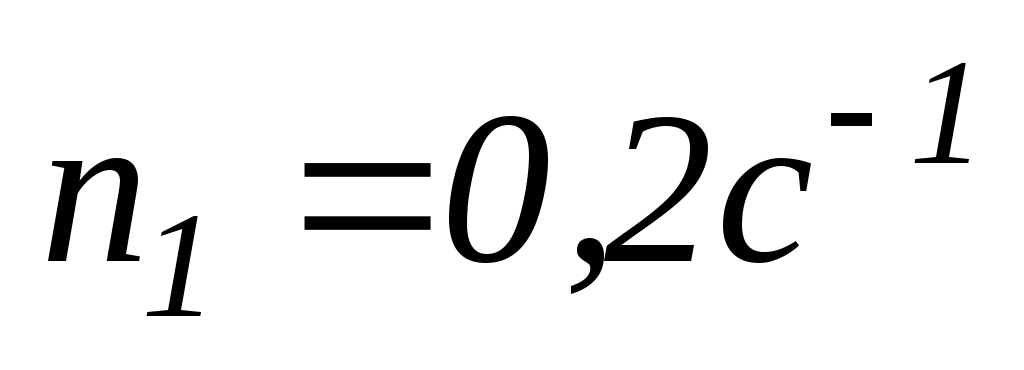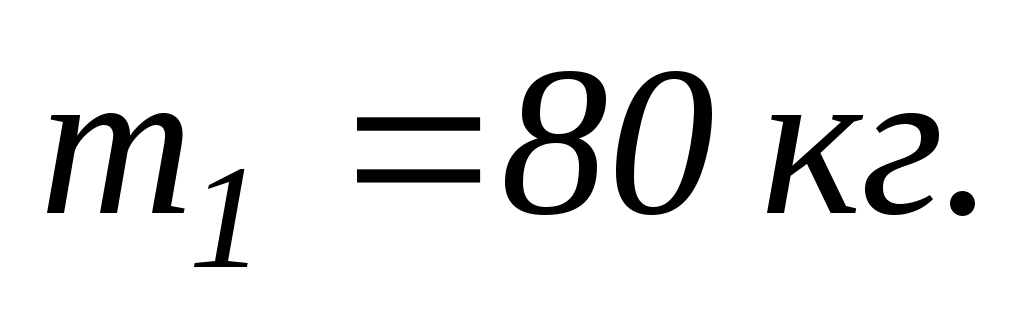
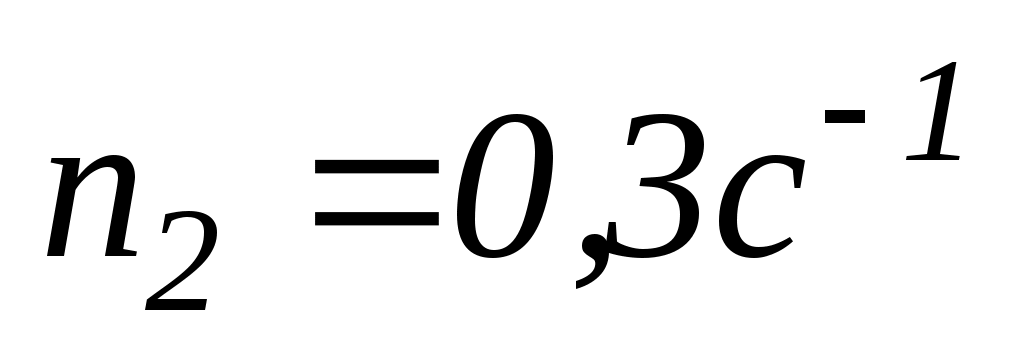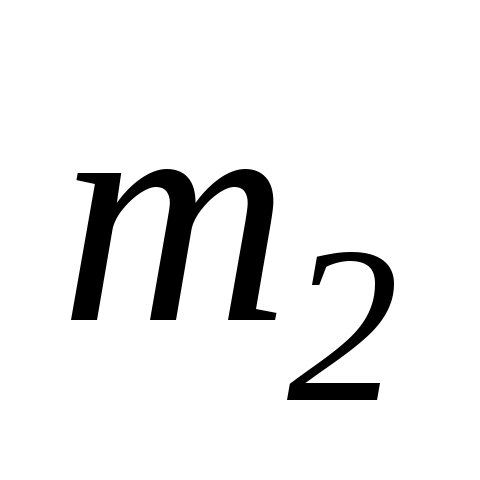
7.5. На краю платформи у вигляді диска, що обертається за інер­цією навколо вертикальної осі з частотою с^-1, стоїть людина ма­сою Коли людина перейшла в центр платформи, вона почала обертатись з частотою с^-1. Момент інерцій людини розрахувати як для матеріальної точки. Визначити масу платформи.

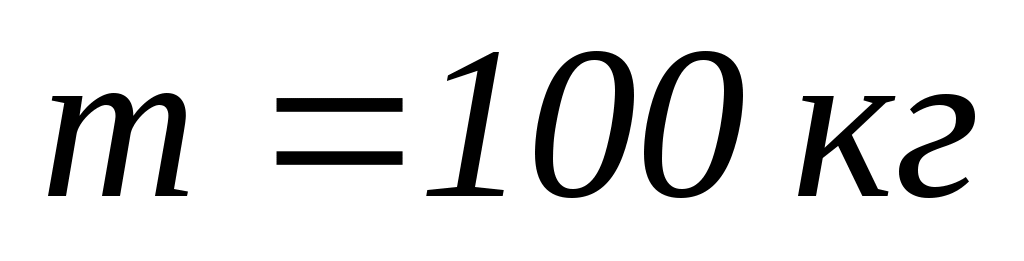
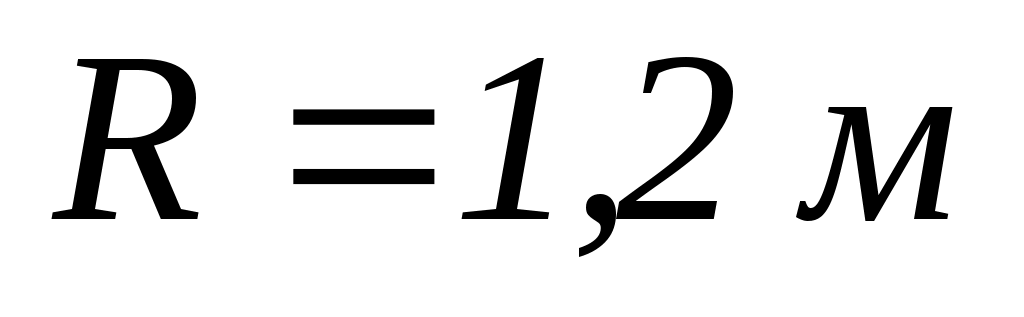
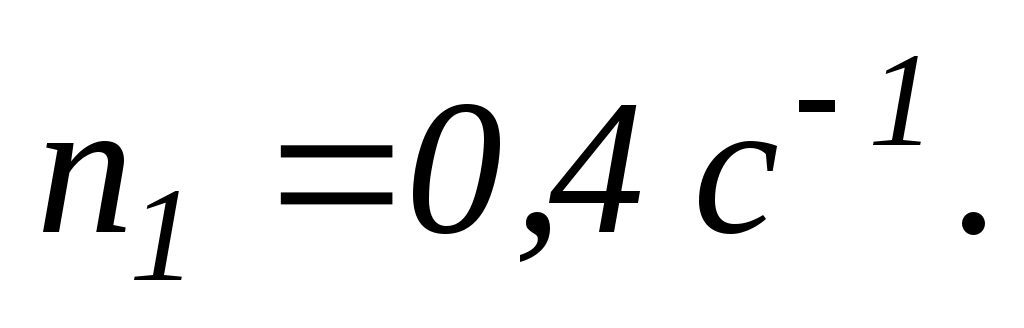
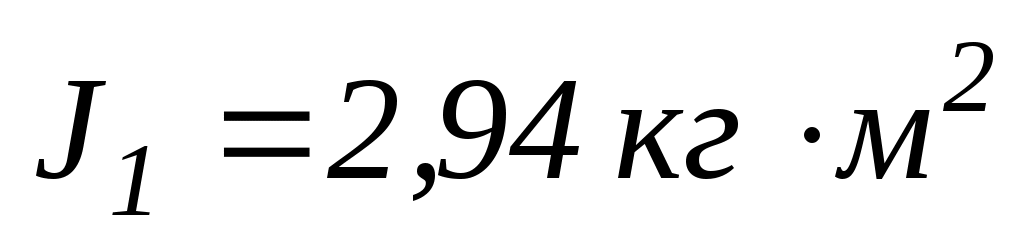
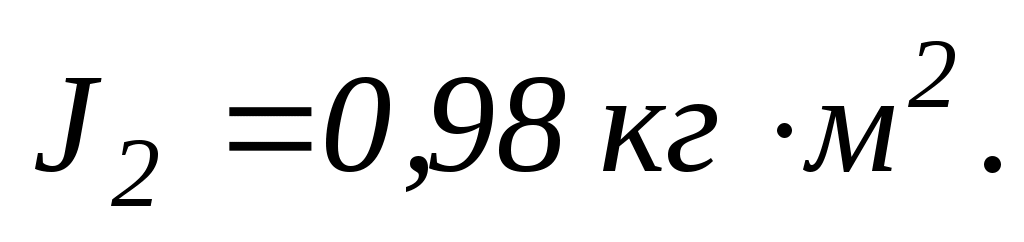
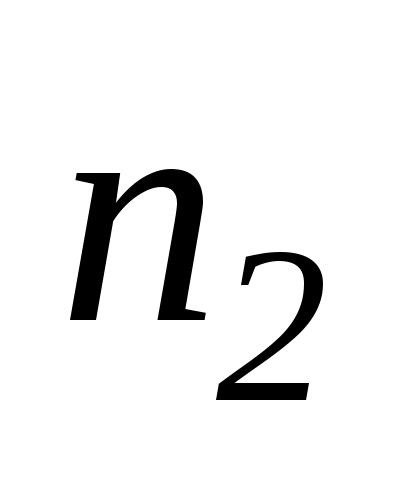
7.6. Горизонтальна платформа масою і радіусом обертається з частотою У центрі платформи стоїть людина і тримає у розведених руках гирі. Платформу вважати однорідним диском. Людина, опустивши руки, зменшує свій момент інерцій від до З якою частотою буде обертатись платформа?

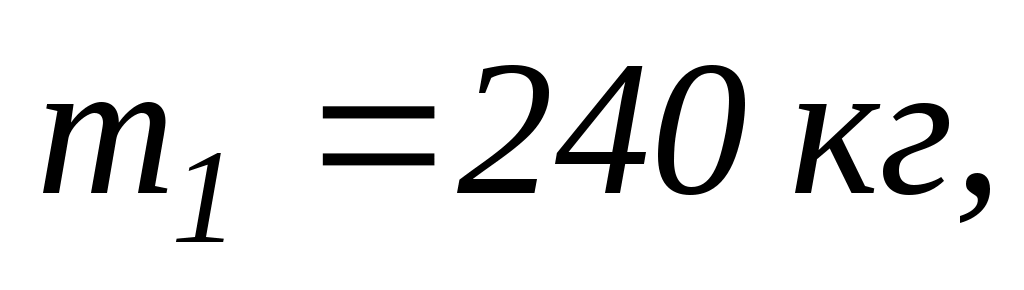
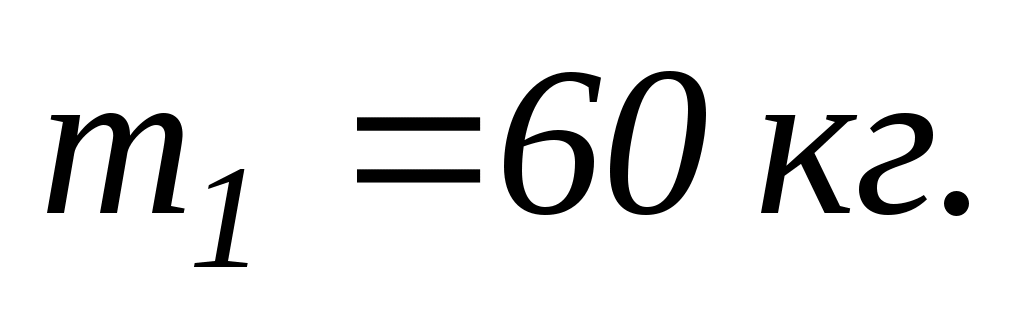
7.7. На краю платформи масою що має форму диска і може обертатись навколо вертикальної осі, стоїть людина масою Момент інерції людини розраховувати як для матеріальної точки. Людина пішла вздовж краю платформи і, обійшовши її, повер­нулась у вихідну точку на платформі. На який кут повернулась плат­форма?

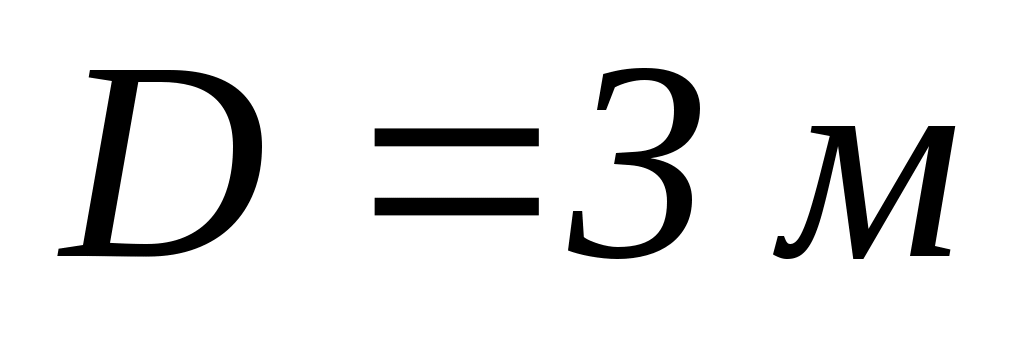
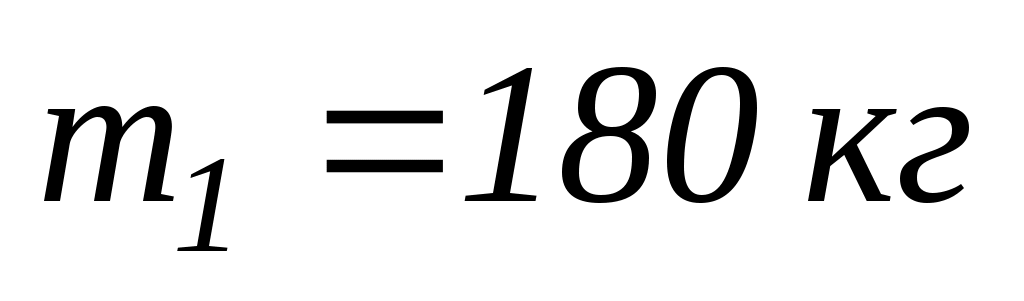
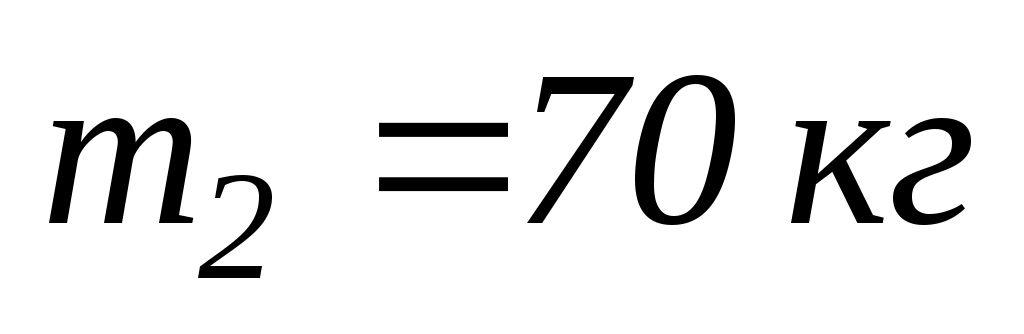
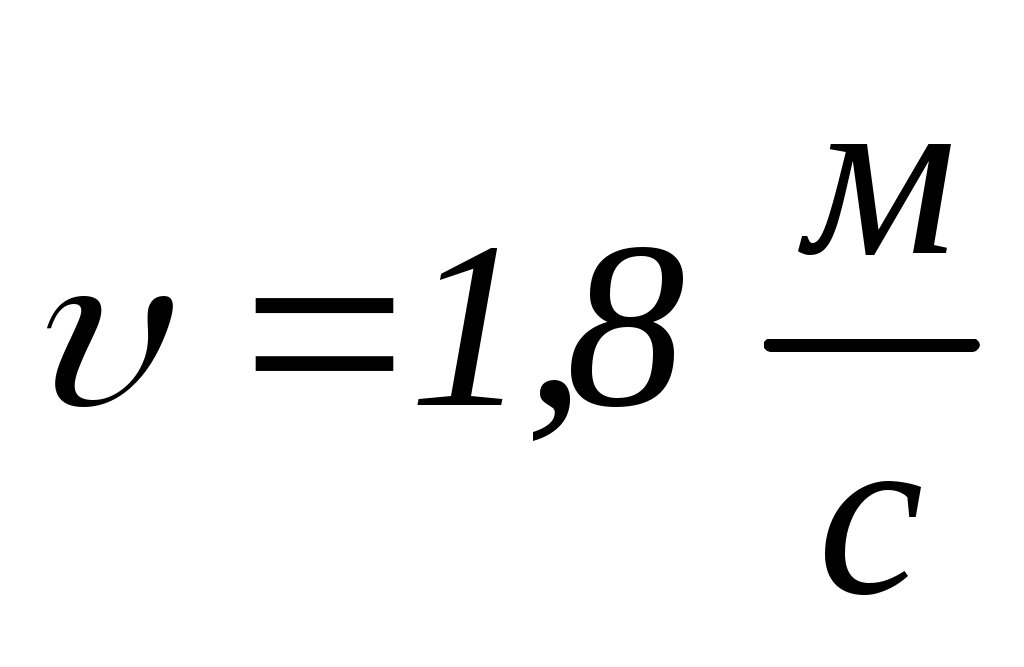
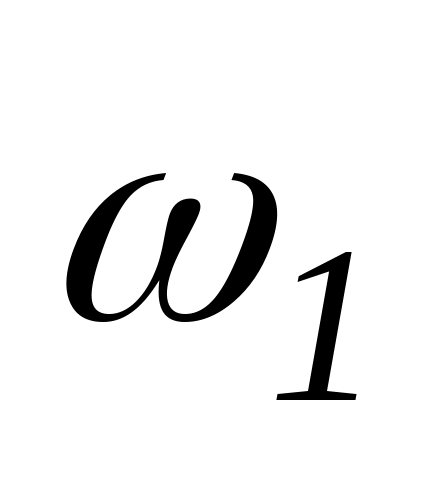
7.8. Платформа у вигляді диска діаметром і масою може обертатись навколо вертикальної осі. По краю плат­форми пішла людина масою зі швидкістю від­носно платформи. З якою кутовою швидкість буде обертатись ця платформа?

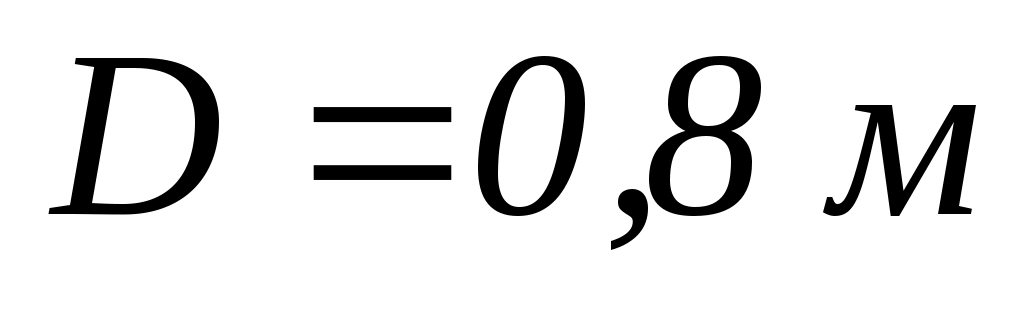
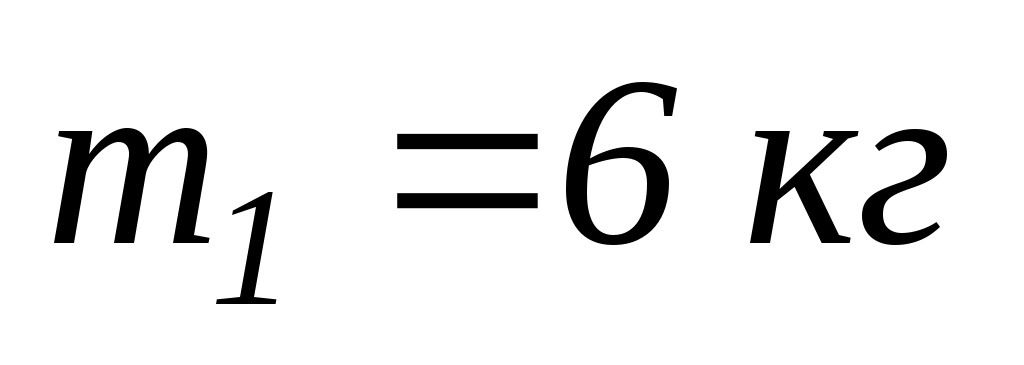
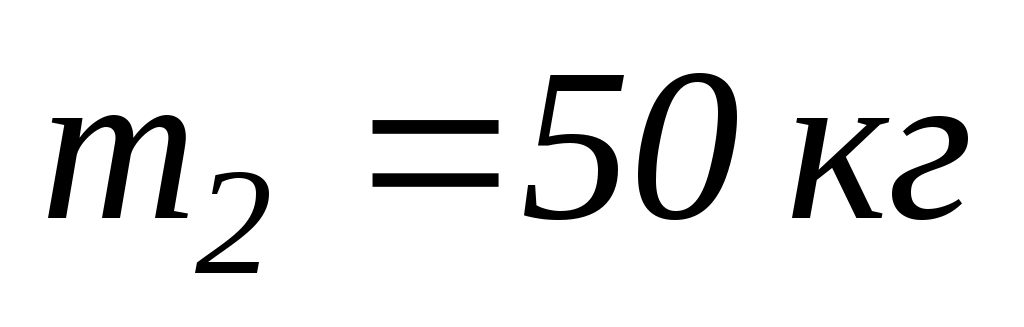
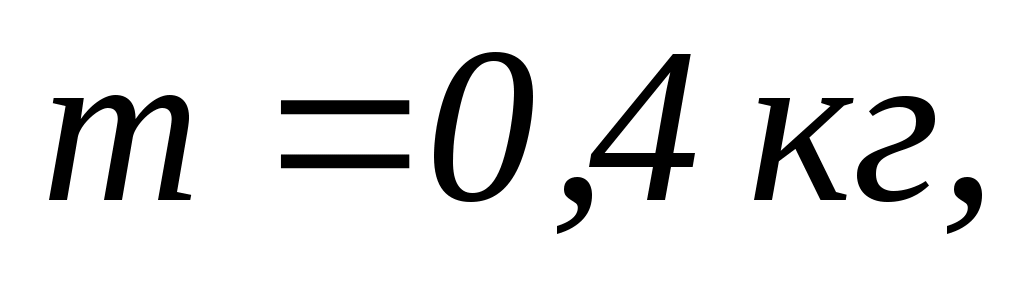
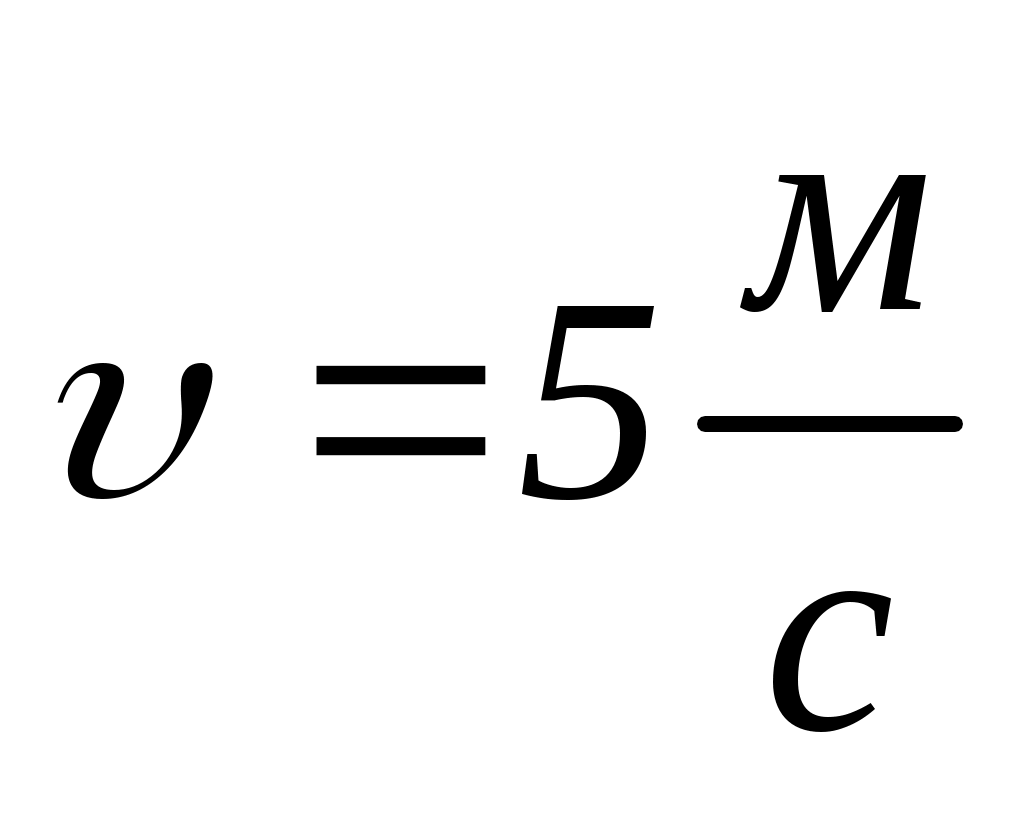
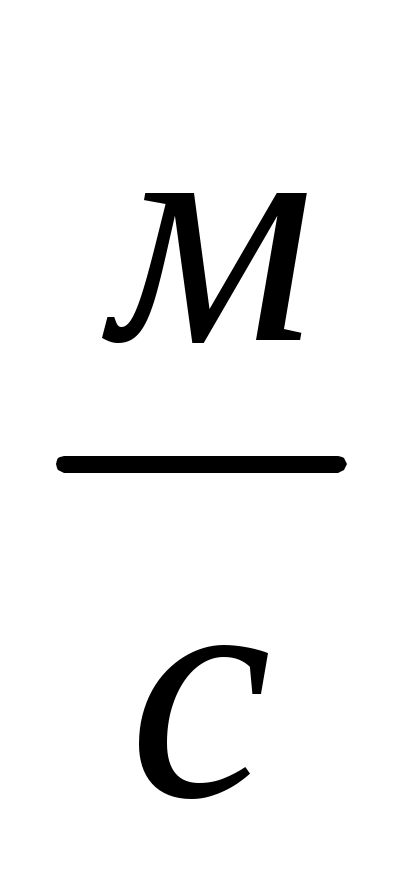
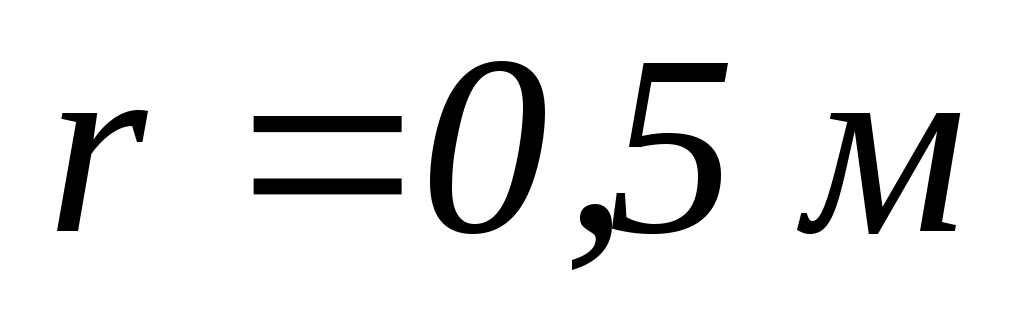
7.9. На краю нерухомої лави Жуковського діаметром і масою стоїть людина масою . Людина піймала м’яч масою що летить зі швидкістю на неї. Траєкторія м’яча горизонтальна і проходить на відстані від осі лави. З якою кутовою швидкістю почала обертатись лава?

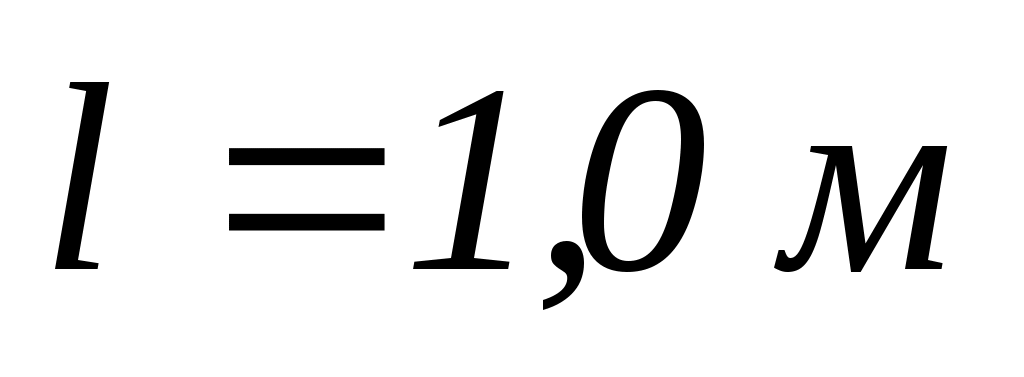
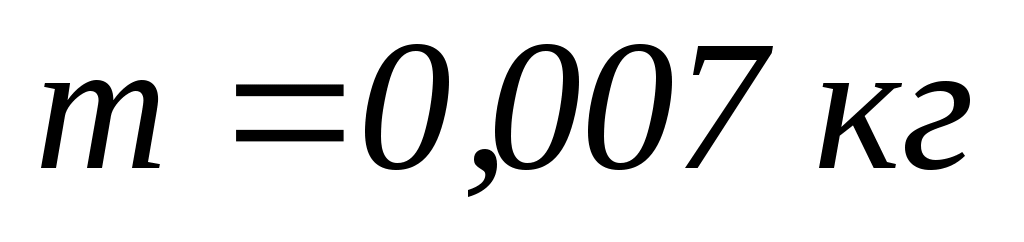
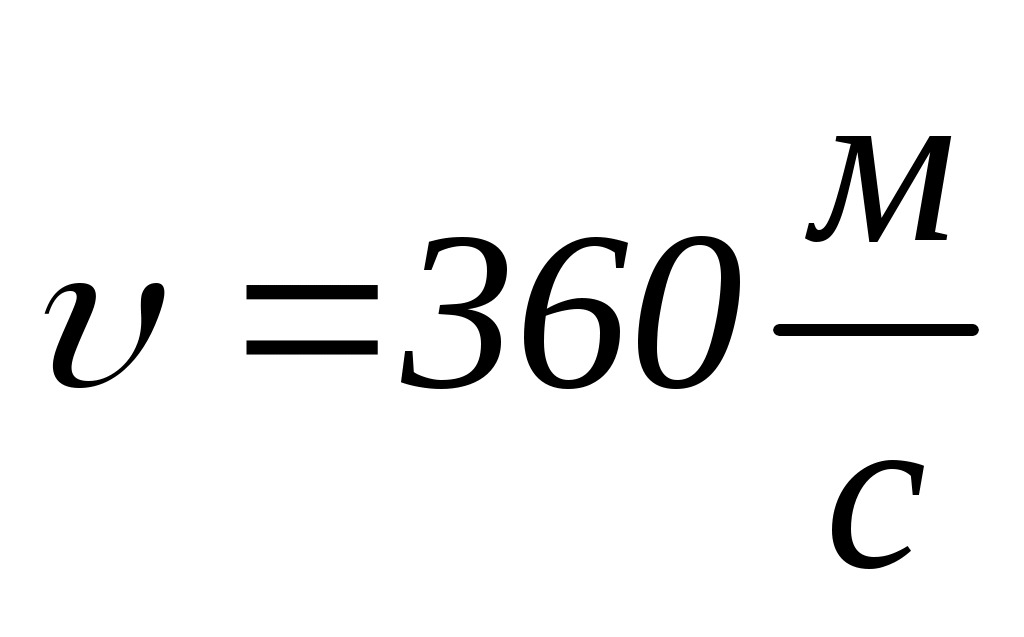
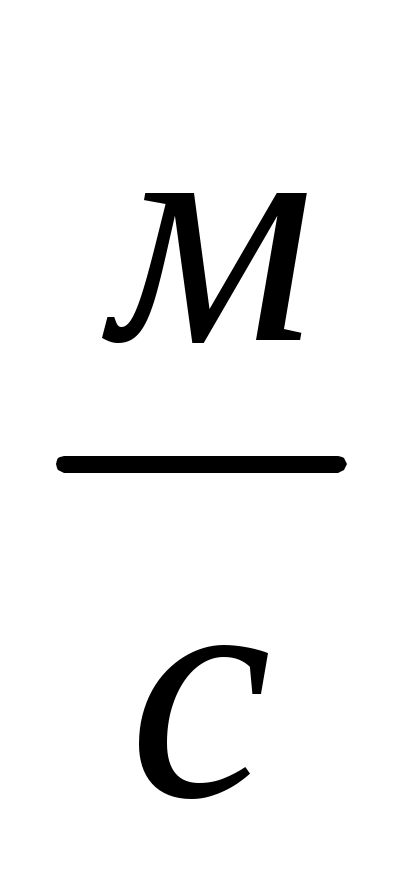
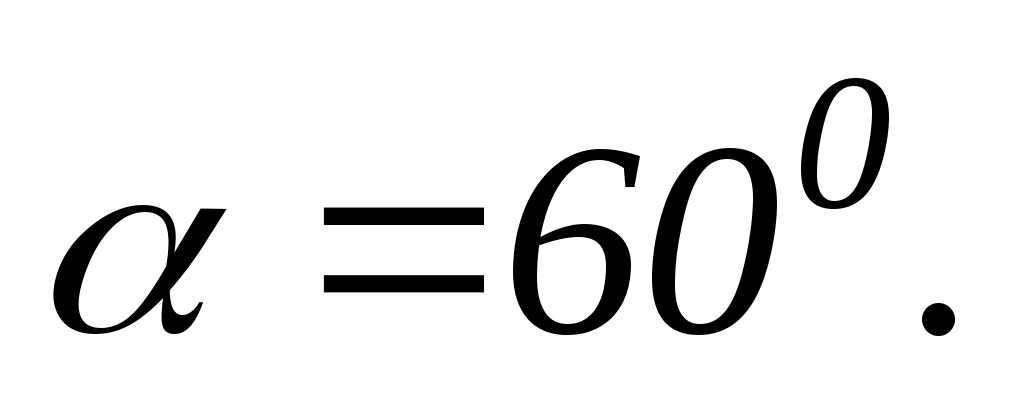
7.10. Однорідний стрижень завдовжки може вільно обер­татись навколо горизонтальної осі, що проходить через один з його кін­ців. В другий кінець абсолютно непружно ударяє куля масою , що летіла зі швидкістю перпендикулярно стрижню і його осі. В результаті стрижень відхилився на кут Визначити масу стрижня.

8. механічні коливання