Механіка. I. механiка кінематика основнi формули

• Название: I. механiка кінематика основнi формули
• Анкор: Механіка
• Дата: 03.11.2020
• Размер: 1.75 Mb.
• Имя файла: I._MEHANIKA.doc
• Тип: Документы; #147829
• страница: 9 из 10

Основні формули

1. Диференціальне рiвняння гармонiчного коливання i його розв'язок

,



де – змiщення точки вiд поло­ження рiвноваги; – амплiтуда коливань; – колова (цик­лiчна) частота коливань; – перiод коливань; – частота;  – початкова фаза.

2. Швидкість і прискорення точки, що виконує гармонічні ко­ливання:





.

3. Повна енергія точки ма­сою , що коливається,

.

4. Диференціальне рiвняння загасаючих коливань i його роз­в'язок





де – коефiцiєнт загасання; – частота коливань, що загасають:



5. Логарифмiчний декремент загасання

æ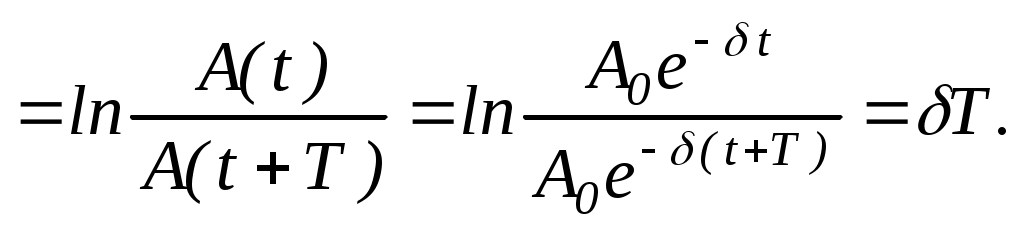

6. Диференційне рiвняння ви­мушених коливань i його розв'язок





де



7. Перiод коливань матема­тичного маятника



де – довжина маятника; – при­скорення вiльного падiння.

8. Перiод коливань пружин­ного маятника



де – маса тiла; – жорсткiсть пружини.

Приклад розв'язання задачі

Частинка масою  кг здiйснює гармонiчнi коливання з перiодом Т = 2 с. Повна енергiя частинки, що коливається,  мДж. Визначити амплi­туду коливань i найбiльшу силу, що дiє на частинку.

Розв'язання

Для визначення амплiтуди коливань використаємо вираз пов­ної енергiї частинки:



де . Звiдси амплiтуда



Оскiльки частинка здiйснює гармонiчнi коливання, то сила, яка дiє на неї, є квазiпружною i може бути виражена спiввiд­ношенням , де – кое­фiцiєнт квазiпружної сили; – змiщення точки, що коливається.

Максимальна сила буде при максимальному змiщеннi



Коефiцiєнт



Тодi





Проведемо обчислення: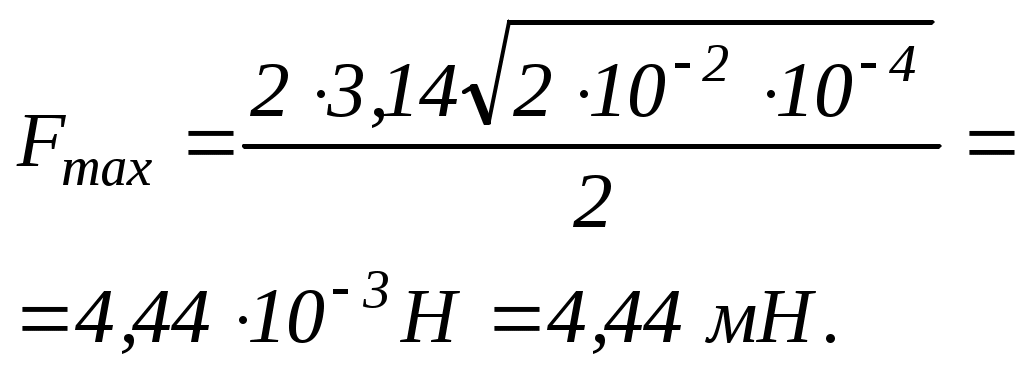

Задачі контрольної роботи

8.1. Матерiальна точка коливається гармонiчно за законом з частотою Амплiтуда коливань Визначити швидкiсть точки в момент часу, коли її змiщення становить

8.2. Матерiальна точка, маса якої коливається гармо­нiчно з частотою . Амплiтуда коливань Визначи­ти максима­ль­ну силу, що дiє на точку.

8.3. Точка здiйснює гармонiчнi коливання, рiвняння яких В момент часу, коли точка мала потенцiальну енергiю на неї подiяла повертальна сила Знай­ти цей момент часу.

8.4. Матерiальна точка здiйснює гармонiчнi коливання так, що в початковий момент часу змiщення а швидкiсть  м/с. Визначити амплiтуду коливань, якщо їх перiод

8.5. Матерiальна точка коливається з частотою гар­монiчно. Амплiтуда коливання дорiвнює початкова фаза Визначити швидкiсть, яку має точка в момент, коли її приско­рення  м/с².

8.6. Матерiальна точка коливається за законом В який момент часу вiдношення її кiнетичної енергiї до потенцiальної дорiвнює одиницi?

8.7. Початкова амплiтуда загасаючого коливання матерiальної точки за вона зменшилась до Через скiльки секунд вона дорiвнюватиме ?

8.8. Логарифмiчний декремент загасання коливань математичного маятника дорiвнює æ Знайти, у скiльки разiв зменшиться амплi­туда коливань за одне коливання маятника та за коливань.

8.9. Математичний маятник завдовжки здiйснює зага­саючi коливання. Через який промiжок часу енергiя коливань маятника зменшиться у раза, якщо логарифмiчний декремент загасання æ ?

8.10. Два однаково спрямовані гармонiчні коливання одного перiоду складаються в одне коливання з амплiтудою Рiзни­ця фаз скла­дових коливань Знайти амплiтуди цих коливань, коли вiдомо, що вони вiдносяться як .

9. гідродинаміка