Раздел 1_РЕД_2. I. основы теории множеств. Системы счисления комбинаторика
 Скачать 9.96 Mb. Скачать 9.96 Mb.
|
|
Глава 3. БИНАРНЫЕ ОТНОШЕНИЯ НА МНОЖЕСТВАХ 3.1. Определение и способы задания отношений Определение. n-местным (n-арным) отношением на множествах X1, X2,…, Xn называют любое подмножество их декартова произведения X1X2…Xn. Поскольку отношения представляют собой множества специального вида, то между ними определены все предметные и логические операции, введенные ранее для обычных множеств. Задание отношения эквивалентно введению на X1X2…Xnнекоторого предиката Р(х1, х2, …, хn)(логического условия), для которого: (Р(х1, х2, …, хn) = true)((х1, х2, …, хn) ). При n = 1отношение называют унарным, смысл его заключается в задании подмножества исходного множества X. В случае n = 2отношение называют бинарным, оно задает на декартовом произведенииX1 X2 множество упорядоченных пар (х,у), где х X1, у X2. Поскольку наиболее распространёнными являются бинарные отношения, у которых X1= X2= X, в дальнейшем будут рассматриваться только отношения на декартовом квадратеX2= X X. При необходимости исходное множество дополнительно указывается нижним индексом:X . Для обозначения бинарных отношений применяется инфиксная система записи, при которой знак отношения помещается между элементами пары. Если пара (х, у) (х X, у X)принадлежит отношению , то это обозначается как хX у, если (х,у) не принадлежит – то ( хX у). Определение. Полным называют отношение, содержащее весь декартов квадратX2 = X X. Обозначается оно UX. Диагональным называют бинарное отношение, содержащее все пары вида (х, х), где х X. Обозначается оно idX. Для единичного исходного множества (X = 1) idX=UX. При X >1 всегда справедливо строгое включение: idXUX. Отношения на конечных множествах могут быть заданы следующими способами. 3.1.1. Перечисление (список пар) В этом случае все упорядоченные пары (х,у), образующие множество, указываются в виде некоторой последовательности (списка). Положение пар в списке может быть любым. Пример 1. Х = Е2 = {0, 1}. Х 2= {(0; 0); (0; 1); (1; 0); (1; 1)}. Зададим отношение списком: = {(0; 0); (1; 0); (1; 1)}. В отношение не включен только один из элементов Х 2— пара(0; 1). 3.1.2. Матрица Декартов квадрат Х 2 = Х Х множества Х, где определено бинарное отношение, может быть задан в виде матрицы, где, например, строки соответствуют первому элементу пары, а столбцы — второму элементу. Если пара (х, у) входит в отношение , то элемент матрицы Р на пересечении строки, соответствующей х, и столбца, соответствующего у, принимается равным 1. Если пара (х, у) не входит в , то данный элемент равен 0. В тех случаях, когда нельзя сказать ни х у ни (х у), в матрице будем ставить прочерк «–». Пример 2. Задать матрицу отношения из примера 1. Решение имеет вид:
Матричное задание отношений более наглядно при изучении их свойств. Для того чтобы ввести отношения на бесконечных множествах, как и при задании самих множеств, необходимо применять и другие способы. 3.1.3. Задание отношений при помощи предикатов Если для отношения , заданного на всем квадрате Х 2 либо его части, возможности всего две (х у либо х у), то такой набор пар элементов (х, у) всегда может быть интерпретирован как область истинности некоторого двухместного предиката Р(х, у), заданного на Х 2, который определяется следующим образом: P(х,y) = true, если х у, иначеP(х,y) = false. Данный прием позволяет во многих случаях довольно просто задавать отношения не только на конечных, но и на бесконечных множествах любой мощности. Пример 3. Отношение из примера 1 можно задать при помощи предиката Р(х,у) = х y, поскольку все пары (х, у), входящие в отношение и только они, удовлетворяют данному условию. Пример 4. Х = R2.Зададим отношение при помощи предиката Р(x, у) = «x больше у». Оно будет образовано парами (x, у)из области истинности предиката Р(x, у), которая на декартовой плоскости будет полуплоскостью, лежащей ниже прямой х = у. Замечание. 1. В ряде случаев при задании отношения с помощью предикатов необходимо дополнительно уточнять условие непринадлежности пары элементов (х, у)отношению — (х у), поскольку отрицание предиката может быть интерпретировано неоднозначно. 2. Будем считать, что в исходном множестве А все элементы – разные и равенство элементов может означать только тождество элемента с самим собой. В случае одинаковых элементов в А для непротиворечивого задания отношения на него необходимо накладывать дополнительные ограничения. 3.2. Аксиомы на отношениях Тип отношений может быть установлен путем проверки справедливости некоторых их элементарных свойств, которые также называют аксиомами. Рассмотрим их общие формулировки, а также структурные свойства отношений, вытекающие из выполнения данных аксиом. 1. Рефлексивность: x X(х х). Запись означает, что для всех элементов xX пары (х, х) принадлежат отношению . При выполнении рефлексивности idA , в отношение входят все пары из одинаковых элементов (х, х), которые в его матрице располагаются на главной диагонали. 2. Антирефлексивность: xX(х х). Для всех xXпары (х, х) не принадлежат отношению . В случае антирефлексивности ни одна из пар idA не входит в отношение. Если не выполняется ни рефлексивность ни антирефлексивность, то это свидетельствует о том, что часть диагонали принадлежит отношению, а часть – нет (либо на ней отношение вообще не определено). 3. Симметричность: x, у X(х у у х). Для всех x, уX из принадлежности пары (х, у) отношению следует принадлежность отношению симметричной ей пары (у, х). Матрица такого отношения симметрична по вхождению пар в него относительно главной диагонали. 4. Антисимметричность: x, уX( (х у)и (у х) х=у). Для всех x,уX из одновременной принадлежности пар (х, у)и (у, х) отношению следует, что х и у — один и тот же элемент. При выполнении антисимметричности: 1) для всех различающихся элементов х и у на симметричных относительно главной диагонали матрицы элементах (х, у), (у, х), вхождение в отношение должно быть противоположным (например, (х у) и (у х)) либо отрицательным, при котором (х у)и (у х); 2) пары из одинаковых элементов (х, х) — на главной диагонали матрицы ― могут как входить, так и не входить в отношение. 5. Асимметричность: x,уX((х у) (у х)). Для всех x,уX из принадлежности пары (х, у)отношению следует, что (у, х) обязательно не принадлежит . Асимметричность – частный случай антисимметричности, отличается от нее тем, что главная диагональ матрицы полностью не входит в отношение, id (иначе для пары (х, х) получим противоречие: (х х) (х х)). Поэтому при выполнении данной аксиомы автоматически выполняется антирефлексивность. 6. Транзитивность: x, у, z X((х у)и (уz) (х z)). Для всех x,у,zX из принадлежности пар (х, у)и (у, z) отношению вытекает принадлежность ему и пары (х, z). Транзитивность означает для всех возможных наборов элементов x,у,z следующее: если пары (х, у)и (у, z)входят в отношение, то пара (х, z), стоящая в матрице отношения на пересечении строки, соответствующей х, и столбца, соответствующего z, также должна входить в отношение. Нарушение данного свойства хотя бы для одной тройки x,у,z (при котором обязательно должны выполняться три условия:(х у), (у z)и(х z)) означает отсутствие транзитивности. В аксиоме транзитивности все три элемента в дальнейшем будем считать различными, иначе аксиома превращается в тривиальные равенства, например, при х = у: (у z) (у z). Отсюда следует, что для отношений на множествах с числом элементов меньше 3, аксиома транзитивности всегда выполняется. Пример 1. Проверить справедливость аксиом 1) —6) для отношения, заданного в примерах 1 — 3. Решение. Проверку проще всего производить по матрице отношения, приведенной в примере 2. 1. Главная диагональ матрицы (пары (0, 0) и (1, 1)) целиком входит в отношение, следовательно, оно рефлексивно и не является антирефлексивным. 2. На двух парах, симметричных относительно главной диагонали ((0, 1) и (1, 0)), вхождение противоположное: 0 1, и 1 0. Других пар недиагональных элементов нет. Поскольку главная диагональ входит в отношение, оно является антисимметричным, но не асимметричным. 3. Как показано выше, при двух элементах в множестве транзитивность выполняется всегда. Ответ: заданное отношение рефлексивно, антисимметрично и транзитивно. Пример 2. Проверить справедливость аксиом 1)—6) для отношения, заданного на множестве Х ={p,q,r}, следующей матрицей:
Решение. 1. Диагональные элементы (p, p), (q, q)входят в отношение, (r, r) — нет, следовательно, для отношения не выполняется ни аксиома рефлексивности, ни аксиома антирефлексивности. 2. На всех парах, симметричных относительно главной диагонали, вхождение противоположное. Поскольку на главной диагонали есть пары, входящие в отношение, оно является антисимметричным, но не асимметричным. 3. Проверим транзитивность. Пары (q,p), (p,r)входят в отношение, пара (q,r) — не входит. Следовательно, транзитивность не выполняется. Ответ: для заданного отношения справедлива только аксиома антисимметричности. 3.3. Основные типы отношений Рассмотрим наиболее употребительные типы отношений. 3.3.1. Отношение эквивалентности Данное отношение удовлетворяет следующим трем аксиомам: 1) рефлексивности, 2) симметричности и 3) транзитивности. Практический смысл отношения эквивалентности заключается в том, что оно разбивает множество, на котором определено, на классы. Определение. Пусть множество Х разбито на подмножества Х1,Х2,..., Хnтаким образом, что все они попарно не пересекаются и объединение их равно Х: 1) Хi= Х, (i=1,...,n); 2) ХiХ, Х jХ , (ij)ХiХ j=. В этом случае говорят, что произведено разбиение Х на классы Х1, ... , Хn. Элементы хi и хj множества Х эквивалентны по отношению к его разбиению, если они принадлежат одному и тому же классу Хk. Замечание. 1. Мощность множества классов эквивалентности может быть как конечной, так и бесконечной (счетной, континуум и т.д.). 2. Смысл понятия эквивалентности в том, что с точки зрения разбиения множества Х элементы хi и хj неразличимы, если попадают в один класс. Обычно отношение эквивалентности обозначают символом « ». Определение. Поэлементным будем называть такое разбиение множества на классы эквивалентности, где каждый класс Хiсодержит ровно один элемент из Х. Фиктивнымбудем называть разбиение в котором выделен один класс Х1, совпадающий со всем Х,(Х1= Х). Пример 1. Рассмотрим в качестве Х множество натуральных чисел N. Его можно разбить отношением эквивалентности на два непересекающихся класса, дающих в сумме все N: множество четных (делящихся на 2 без остатка) чисел N2 и множество нечетных (делящихся на 2 с остатком 1) чисел N2. При этом само множество пар отношения будет образовано: а) всеми парами четных чисел; б) всеми парами нечетных чисел. Смешанные пары (четное число с нечетным и наоборот) в него не войдут. Данное отношение эквивалентности можно задать при помощи предиката Р(х, у) =«х - у кратно 2». Пример 2. Х = N. Х1 ={1}, Х2 ={2, 3}, Х3 = {4, 5, 6, 7},…, Хi = {множество целых чисел от 2i-1до2i–1}. Выделенные множества Х1,Х2, ... не пересекаются, объединение их равно N. Следовательно, они разбивают N на классы. Их число бесконечно. Несложно показать, что { Хi }=0. Множество пар, составляющих отношение, будет следующим: {(1, 1); (2, 2); (2, 3); (3, 2); (3, 3); (4, 4); (4, 5); (4, 6); (4, 7); (5, 4); (5, 5); (5, 6)…}. Отношение можно задать при помощи предиката, непосредственно задающего структуру классов эквивалентности: Р(х,у)=«2i-1 ≤ х, у ≤2i-1, iN». Пример 3. Х = {1, 2, 3, 4, 5, 6}. Ниже приведены при помощи матриц примеры отношений, реализующих следующие разбиения Х на классы: 1) разбиение: Х1={1,2}, Х2={3}, Х3={4, 5, 6};2) фиктивное: Х1= Х ; 3) поэлементное: Х1={1}, Х2 ={2}, Х3={3}, Х4 = {4}, Х5 ={5}, Х6={6}.
3.3.2. Отношение нестрогого (частичного) порядка При данном отношении справедливы аксиомы: 1) рефлексивности, 2) антисимметричности; 3) транзитивности. Отношение нестрогого порядка задает некоторый способ сравнения элементов на рассматриваемом множестве таким образом, что для каждого его элемента х пара (х, х)также принадлежит отношению. Данные отношения обычно обозначают символом , так как на числовых множествах нестрогий порядок может быть задан предикатом «х меньше или равен у». Если х у, то говорят, что х подчинен у либо х не превосходит у. Определение. Множества, на которых введено отношение нестрогого (частичного) порядка, называют частично упорядоченными. Частичный порядок на Xназывается линейным, если все пары элементов из X сравнимы, т.е. для любых х, у Xможно выяснить (х у) либо(у х). Пусть Х — частично упорядоченное множество. Наименьшим называют элемент аХ, который подчинен (не превосходит) всех остальных элементов X, т.е.хX(х а). Наибольшим называют элемент аХ, которому подчинены все остальные элементы из X— хX(х а).Обозначаются наименьший и наибольший элементы как minХ и mахХ. У линейно упорядоченного множества любое подмножество также является линейно упорядоченным. Пример 4. Рассмотрим в качестве исходного множество натуральных чисел N. Зададим на нем два варианта отношения нестрогого порядка с помощью предикатов: 1) Р(х, у) = «х у» , 2) Р(х, у)= «х делится без остатка на у». Оба отношения удовлетворяют аксиомам рефлексивности, антисимметричности и транзитивности. Первое отношение задает на N линейный порядок, поскольку оно определено для всех пар натуральных чисел. Наименьший элемент minХ= 1, наибольшего не существует. Второе отношение не обеспечивает на N линейный порядок, поскольку существуют пары несравнимых натуральных чисел. Например, (2, 3), (4, 5) и т.д. Наименьшего и наибольшего элементов нет. 3.3.3. Отношение строгого порядка Отношение данного типа задает способ сравнения элементов на множестве Х таким образом, что все возможныепары элементов (х, х)не принадлежат отношению. Данные отношения обозначают символом « < », так как на числовых множествах строгий порядок может быть задан предикатом «х строго меньше у». Для определения отношения строгого порядка достаточно проверить на парах элементов, составляющих его, справедливость только двух аксиом: 1) асимметричности и 2) транзитивности. Замечание. Зачастую в число аксиом отношения строгого порядка включают аксиому антирефлексивности. Однако, как показано выше, справедливость данной аксиомы следует из выполнения асимметричности. По аналогии с частичным (нестрогим) порядком, множества, на которых введено отношение строгого порядка, называют строго упорядоченными. Данный порядок на Xназывается линейным, если все пары элементов из X сравнимы. Пример 5. Рассмотрим для множества Х = Е2 ={0,1} булеан [Х] = {(); (0); (1); (0;1)}. Через{х}i будем обозначать подмножества Х в порядке их вхождения в [Х]. Введем на множестве[Х]отношения строгого и нестрогого порядка соответственно при помощи предикатов: а) Р({х}i , {х}j) = «{х}i{х}j (подмножество {х}iстрого входит в подмножество {х}j )»; б) Q({х}i ,{х}j) = «{х}i{х}j (подмножество {х}iнестрого входит в подмножество {х}j )». Если отрицаниям данных предикатов придать естественный смысл обратного включения: Р({х}i ,{х}j) = «{х}j {х}i» и Q({х}i,{х}j) = «{х}j {х}i», то оба отношения будут вводить на [Х]соответственно частичный и строгий порядок. Оба порядка не будут линейными, поскольку не позволяют сравнить между собой {х}2 = (0)и {х}3 = (1). Матрицы отношений будут следующими:
Замечание. Если в Примере 5 в качестве отрицаний предикатов, задающих отношения, принять: Р({х}i ,{х}j) = «{х}j {х}iили {х}j не сравнимо с {х}i», Q({х}i,{х}j) = «{х}j {х}i или {х}jне сравнимо с {х}i», то данные отношения будут задавать полный порядок. 3.4. Проверка типов отношений. Решение задач Для строгого доказательства принадлежности введенного на некотором множестве Х бинарного отношения тому или иномутипу необходимо проверить справедливость выполнения всех аксиом данного типа для всех возможных упорядоченных пар (х, у) Х2. Для доказательства того, что бинарное отношение на множестве Х не принадлежит к рассматриваемому типу, достаточно указать хотя бы один случай нарушения какой-либо из аксиом данного типа отношений на элементах из Х. Пример 1. Рассмотрим множество всех треугольников {Т}, заданных длинами их сторон(a, b, c)(a, b, c—вещественные числа). Проверить, будет ли устанавливать нестрогий порядок на {Т} отношение TiTj = «периметр Тiне меньше периметра Тj». Решение. Обозначим периметр треугольника Тiчерез Р(Тi). Для отношения нестрогого порядка должны выполняться аксиомы рефлексивности, антисимметричности, транзитивности. 1. Рефлексивность. Тi{Т} (Р(Тi) Р(Тi))означает: «периметр Р(Тi) каждого треугольника Тiне меньше Р(Тi)». Данное условие выполняется для всех элементов {Т}, поскольку для каждого Р(Тi)как для вещественного числа справедливо равенство Р(Тi)= Р(Тi). 2. Антисимметричность. Выполнение аксиомы у заданного отношения для любых треугольников Tiи Tjсводится к выполнению условия «если Р(Тi)≤ Р(Тj)и Р(Тj)≤ Р(Тi), то Ti= Tj», т.е. Ti иTj— один и тот же элемент. Очевидно, оно нарушается, поскольку можно привести пример двух треугольников с одинаковыми периметрами, у которых не совпадают длины сторон. Ответ: предложенное отношение не является отношением нестрогого порядка на множестве {Т}, поскольку у него не выполняется аксиома антисимметричности. Замечание. В рассмотренном примере 1 справедливость аксиомы транзитивности можно не проверять, так как отрицательный ответ уже получен. Пример 2. Выяснить, какой тип отношений вводит на множестве всех множеств U предикат Р(Х, Y)= «мощность множества Х равна мощности множества Y(Х=Y)» ? Решение. 1.Отношение является рефлексивным, поскольку мощность любого множества равна самой себе:XU(X X). 2. Аксиома симметричности также выполняется, поскольку равенство мощностей множеств не зависит от порядка их упоминания — для X,YU из равенства Х=Yследует Y=Х. 3. Транзитивность. Допустим, для некоторых множеств Х, Y, Zсправедливо:Х=Y,Y=Z. Для доказательства транзитивности необходимо сначала доказать, чтоХ=Z. По определению эквивалентных множеств из Х=Y,Y= Zследует, что существуют взаимно однозначные отображения f: ХYи g:YZ. Композиция h = gf, переводящая Х в Z, по свойству взаимно однозначных отображений также будет взаимно однозначна. Отсюда получим, что Х=Z, что и требовалось доказать. Так как для рассмотренного отношения справедливы аксиомы рефлексивности, симметричности и транзитивности, то оно является отношением эквивалентности. Ответ: заданный предикат вводит на множестве всех множеств U отношение эквивалентности. ЗАДАЧИ 1. Проверить справедливость всех рассмотренных аксиом для отношений, заданных следующими матрицами: а) б)
2. На множестве нечетных арабских цифр задать следующие бинарные отношения: а) рефлексивное и не транзитивное; б) антирефлексивное и симметричное; в) задающее строгий порядок; г) антирефлексивное и асимметричное, д) антисимметричное и не транзитивное. 3. На множестве из трех элементов {a,b,c} задать при помощи списков или таблиц бинарные отношения следующего типа: а) эквивалентности (отличное от поэлементного и фиктивного); б) строгого порядка; в) нестрогого порядка. 4. На множестве простых чисел в интервале [0; 10] построить примеры отношений: а) антирефлексивного, симметричного и не транзитивного; б) транзитивного, но не антисимметричного. 5. Проверить, будут ли разбивать на классы множество N: а) подмножества N0 , N1 , ... , Nk -1 , состоящие соответственно из чисел, имеющих остаток 0,1,...,k–1 при делении на заданное натуральное число k; б) подмножества {1}, N2 , N3 , N4 , … , состоящие, соответственно, из числа 1 и чисел, делящихся без остатка на 2, 3, 4,...; в) подмножества N(1), N(2) , N(3), ... , состоящие из чисел, которые можно представить в виде произведения, состоящего соответственно из одного, двух, трех и т.д. простых чисел, отличных от 1. 6. Будет ли задавать отношение эквивалентности на множестве рациональных чисел в интервале [0, 1]: а) объединение рациональных чисел в классы, если их можно представить дробью с одинаковым знаменателем; б) объединение рациональных чисел в одинаковые классы, если их можно представить в виде несократимой дроби с одинаковым знаменателем. 7. Ввести отношения эквивалентности, строгого и нестрогого порядка на множествах: а) всех кругов на плоскости, заданных декартовыми координатами центра и радиусом, б) всех прямых на плоскости, заданных в декартовых координатах канонической формулой ax+by+c=0. 8. Дано множество V всех векторов двухмерного евклидового пространства Е2, в котором скалярное произведение векторовv = (a,b) иv= (a,b) определено как (v,v)= (aa+ bb). Выяснить, будут ли задавать отношение эквивалентности на V следующие предикаты: а) Р(v,v) = «(v,v) <0»; б) Р(v,v) = «(v,v)0». 9. На булеане множества {, , } ввести отношения: а) эквивалентности (отличное от поэлементного и фиктивного); б) строгого порядка. 10. На множестве целых чисел в интервале Х = [0; 10] построить примеры отношений строгого порядка, которые: а) задают линейный порядок на Х, б) не обеспечивают линейный порядок на Х . 11. На множестве F всех функций одной переменной, определенных на отрезке [a, b], отношение задано предикатом P(f1, f2)= «x[a, b]( f1(х) ≤f2(х) )». Доказать, что данное отношение вводит на F частичный порядок. Проверить, будет ли этот порядок линейным. Существуют ли при данном порядке наименьший и наибольший элементы? КОНТРОЛЬНЫЕ ЗАДАНИЯ ПО ТЕМЕ I. ОБЩАЯ ТЕОРИЯ МНОЖЕСТВ В.1. 1. Выразить с помощью теоретико-множественных операций в виде формулы заштрихованное множество на диаграмме Венна:  2. Построить взаимно однозначное отображение множества натуральных чисел N на множество рациональных чисел из интервала [0,2]. В.2. 1. Доказать по методу математической индукции, что: 1 + 4 + 7 + … + (3n- 2) = n·(3n- 1)/2. 2. Доказать второй закон де Моргана алгебры множеств. В. 3. 1. Изобразить на полной диаграмме пересечений Венна множество, задаваемое формулой В (A В С). 2. Привести на множестве Х = {0,1} примеры двух отношений: а) антирефлексивного и симметричного, б) не рефлексивного, не антирефлексивного, но антисимметричного. В. 4. 1. Доказать по методу математической индукции, что при любых натуральных n справедливо: 42n+5n–1кратно 20. 2. Проверить (доказать или опровергнуть), будет ли формула (А В) (А\В) теоремой алгебры множеств. В. 5. 1 Проверить (доказать или опровергнуть), будет ли формула (AB) (А B)теоремой алгебры множеств. 2. Проверить, будет ли отношением эквивалентности на множестве натуральных чисел N отношение, задаваемое предикатом Р(х, у)=” х2+ у2= 25“. В. 6. 1. Выразить с помощью теоретико-множественных операций в виде формулы заштрихованное множество на диаграмме Венна:  2. Привести собственный пример множеств А и В и отображения f:AB, которое является сюръективным, но не инъективным. Ответ обосновать. В. 7. 1. Доказать по методу математической индукции, что при любых натуральных n выражение 22n+32n-1кратно 6. 2. Проверить (доказать или опровергнуть), будет ли формула (AB) А В теоремой алгебры множеств. В. 8. 1. Выразить с помощью теоретико-множественных операций в виде формулы заштрихованное множество на диаграмме Венна: 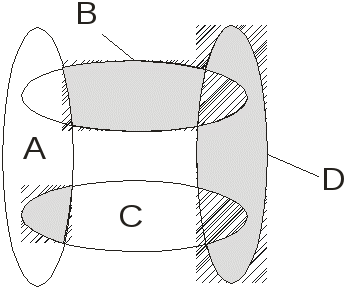 2. Доказать эквивалентность множества точек трехмерного шара единичного диаметра и множества точек куба с единичной длиной ребер. В.9.1. Привести пример формул составных множеств F1(А,В,С),F2(А,В,С)таких, что равенствоF1(А,В,С) =F2(А,В): а) выполняется для попарно непересекающихся исходных множеств А, В, С иб) не выполняется для пересекающихся А,В,С . 2. Найти мощность множества точек на одном витке спирали c радиусом R и шагом Р, задаваемом параметрическим уравнением: x = Rsint, y = Rcost, z = Pt, 0 t 2. В. 10. 1. Изобразить на полной диаграмме пересечений Венна множество, задаваемое формулой А В(A (С\В)). 2. Ввести отношения а) строгого и б) нестрогого порядка на множестве векторов на евклидовой плоскости. Исследовать линейность порядков, наличие наименьшего и наибольшего элементов. В. 11. 1. Привести примеры непустых множеств А, В и С, для которых формула А В С = С : а) справедлива и б) несправедлива. 2. Найти мощность точек плоскости, ограниченное эллипсом 4х2+у2=1. В. 12. Можно ли придумать пример множества А, для которого не выполняется закон исключения третьего? Ответ обосновать. 2. Будут ли задавать отношение эквивалентности на множестве натуральных чисел N предикаты: а) Р(х,у)=”х- у=1“, б) Q(х,у)=”х- у=0“. В.13. 1. Доказать по методу математической индукции, что при любых натуральных n справедливо: 0 + 2 + 6 + … +(n2 - n) = n·(n2 -1)/3. 2. Можно ли построить взаимно однозначное отображение множества чётных натуральных чисел N2 на множество вещественных чисел из интервала [0; 0,1] ? Ответ обосновать. В. 14. 1. Изобразить на полной диаграмме пересечений Венна множество, задаваемое формулой (B\A) (С А\B). 2. Привести пример отображения на множестве геометрических фигур, которое однозначно, но не взаимно однозначно. В.15. 1. Привести пример непустых множеств А,В,С, для которых (АВ, АС, ВС) и одновременно справедливы формулы А В С = С , А В С = А . 2. Проверить (доказать или опровергнуть), будет ли формула A\B Aтеоремой алгебры множеств. В. 16. 1. Доказать по методу математической индукции, что разность 32n-5nпри любых натуральных n 2 кратна 4. 2. Ввести отношение частичного порядка на множестве квадратичных парабол на плоскости, задаваемых формулой у = ах2 + bx+c . Исследовать линейность порядка, наличие наименьшего и наибольшего элементов. В. 17. 1. Изобразить на полной диаграмме пересечений Венна множество, задаваемое формулой (А В ) С. 2. Заданы множества Х = {, , O} и Y= {a,b,c}. Построить декартовы произведения ХY,Y Х и декартов квадрат Х2. В. 18. 1. Выразить с помощью теоретико-множественных операций в виде формулы заштрихованное множество на диаграмме Венна: 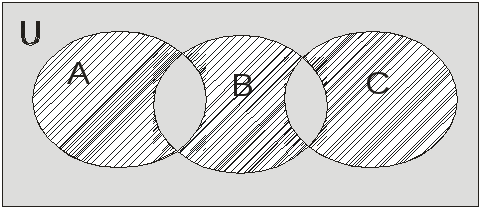 2. Доказать справедливость для любых множеств А и В следующего соотношения: если А В, то В А. В. 19. 1. Проверить (доказать или опровергнуть), будет ли формула (А В) А теоремой алгебры множеств. 2. Привести пример взаимно однозначного отображения множества натуральных чисел N на декартов квадрат N2 . В. 20. 1. Изобразить на полной диаграмме пересечений Венна множество, задаваемое формулой В (A С В). 2. Можно ли построить взаимно однозначное отображение множества вещественных чисел из [0; 1] на множество рациональных чисел из интервала [-; + ]? Ответ обосновать. В.21. 1. Изобразить на полной диаграмме пересечений Венна множество, задаваемое формулой А (В С). 2. Привести на множестве Х = {А,B, C,D} пример отношения, которое рефлексивно, симметрично, но не транзитивно. В. 22.1. Доказать по методу математической индукции, что при любых натуральных n справедливо неравенство: 12 + 32 + 52 + 72 +…+(2n-1)2n (2n-1) (2n+1)/3. 2. На декартовом квадрате множества Х = {0; 1; 2} задать при помощи предиката отношение эквивалентности, разбивающее Х2на два класса эквивалентности. В. 23.1. Выразить с помощью теоретико-множественных операций в виде формулы заштрихованное множество на диаграмме Венна:  2. Привести примеры непустых множеств А и В, для которых формула А В = А: а) выполняется и б) не выполняется. В. 24. 1. Привести пример двух формул составных множеств F1(А, В, С),F2(А, В, С)таких, что: а) для попарно непересекающихся исходных множеств А, В, С выполняется равенствоF1(А, В, С)=F2(А, В, С) , б) для пересекающихся А, В, С выполняется строгое включение F1(А, В, С) F2(А,В,С) . 2. Привести собственный пример множеств А и В и отображения f : AB, которое является инъективным, но не сюръективным. Ответ обосновать. В. 25.1. Для множеств Х = {α,, } и Y= {1; 2; 3; 4}. Построить следующие декартовы произведения: ХY,Y Х, Х3и Y2. 2. Найти мощность множества точек на гиперболе у = 1/(х-2) при х (3; +). В. 26. 1. Изобразить на полной диаграмме пересечений Венна множество, задаваемое формулой (А B) С . 2. Привести на множестве Х = {, , O} пример отношения, которое антирефлексивно и не транзитивно. В. 27. 1.Проверить, будут ли приведенные ниже записи формулами алгебры множеств: а) А В А В, б) (BС) =A,в) А В В. Ответ обосновать. 2. Проверить справедливость аксиом для отношения на множестве Х = {0; 1; 2; 3}, заданного таблицей
|
