4.2.4. Перевод целого числа из двоичной системы счисления
в систему с основаниемp = 2s
При переводе целого числа все его цифры в разрядах двоичной записи числа, начиная с младших (стоящих справа), разбивают на группы длины s. Если последняя группа получилась длины, меньшей s, ее спереди дополняем незначащими нулями. Затем двоичные числа в полученных группах заменяют цифрами в системе с основанием p = 2s и объединяют в одну запись, которая и является искомым выражением.
Пример 8. Перевести в шестнадцатеричную систему счисления двоичное число 10110100112.
Решение. 16 = 24, s = 4. Разбиение на группы длины s = 4 с дополнением первой группы из двух цифр двумя незначащими нулями дает следующие двоичные числа: 0010, 1101, 0011.
Заменяем их числами в шестнадцатеричной системе счисления: 00102 = 216, 11012 = D16, 00112 = 316 и записываем слитно. В итоге получаем искомую запись числа: 10110100112 = 2D316.
Пример 9. Перевести в четверичную систему счисления двоичное число 111011110002.
Решение. 4 = 22, s = 2. Разбиение на группы длины s = 2 с дополнением первой группы одним незначащим нулем дает следующие двоичные числа: 01, 11, 01, 11, 10, 00.
Заменяем их числами в четверичной системе счисления: 012 = 14,112 = 34,012 = 14,112 = 34,102 = 24,002 = 04 и записываем слитно. В итоге получаем искомую четверичную запись числа: 111011110002 = 1313204.
4.2.5. Представление двоичной байтовой информации в шестнадцатеричной и десятичной системах
Несмотря на то, что на элементарном уровне физическая память вычислительных устройств имеет битовую структуру, в качестве минимальной адресуемой единицы памяти в современных процессорах и алгоритмических языках принят байт – группа из 23=8 подряд стоящих битов. Каждому байту памяти соответствует уникальный адрес – некоторое целое положительное число. Кроме того, аппаратные и программные средства позволяют одновременно работать с группами, содержащими 2, 4, 8 и более байтов.
Содержимое байта в двоичной системе можно представить двоичным
8-разрядным числом в диапазоне от 0 до 28 –1 = 255. Для сокращения записи, а также для сокращения действий при переводе содержимое байтов разбивают на две группы по 4 бита – тетрады, каждую из которых можно представить шестнадцатеричным числом, которое может принимать значения из множества {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F}.
Пример 10. Перевести в шестнадцатеричную систему счисления двоичное число, задающее содержимое байта: 110010112.
Решение. Разбиваем байт на две тетрады: 11002 и 10112. Применяя замены 11002 = 1210 = С16, 10112 = 1110 = В16, получим: 110010112 = СВ16.
Также шестнадцатеричные числа, формат представления которых есть в основных алгоритмических языках, используют на практике для засылки битовых значений в байтовые массивы. В этом случае двоичную информацию переводят в 16-ричную форму и присваивают данные значения соответствующим байтовым переменным.
Пример 11. Найти 16-ричное число, которое обеспечивает установку в единицу разрядов 0, 3, 5 и 7 байта.
Решение. По сформулированному условию вначале составляем двоичное битовое содержимое байта: 101010012. Переводя тетрады в шестнадцатеричную систему (10102 = А16, 10012 = 916), получим искомое 16-ричное число: 101010012 = А916.
В десятичную форму двоичную байтовую информацию переводят при работе с кодами символов, адресами в компьютерных сетях и др. случаях. Данный переход для сокращения действий проще выполнять через 16-ричную систему счисления. Из двоичной формы в 16-ричную числа переводят по сокращенным правилам, из 16-ричной в десятичную систему перевод производится по общим правилам.
Пример 12. Перевести в десятичную систему IP-адрес, состоящий из 4 октетов (байтов), разделенных точками:
00110110.10110111.11010001.111001012.
Решение. Записываем развернутую форму представления октетов по степеням основания 2, выражаем полученные степени в десятичной системе счисления и суммируем:
001101102 = 125 + 124 + 122 + 121 = 3210 + 1610 + 410 + 210 = 5410
101101112 = 127 + 125 + 124 + 122 + 121 + 120 = 12810+ 3210 + 1610 + 410 + 210 + 110 = 18310
110100012 = 127 + 126 + 124 + 120 = 12810 + 6410 + 1610 + 110 =
= 20910
111001012 = 127 + 126 + 125 + 122 + 120 = 12810 + 6410 + 3210 + 410 + 110 = 22910
Объединяя полученные десятичные числа, получим искомое десятичное представление IP-адреса:
00110110.10110111.11010001.111001012 = 54.183.209.22916.
4.3. Дробные и смешанные числа в позиционных системах счисления с постоянными основаниями
В позиционных системах счисления вещественные числа представляют при помощи целой и дробной частей, разделенных между собой запятой. И целую часть и дробную записывают при помощи последовательности отдельных знаков, стоящих в разрядах – местах, за которыми закреплен порядковый номер, отсчитываемый от запятой. В целой части отсчет идет от разделяющей запятой справа – налево от 0 и выше. Дробная часть изображается в разрядах, стоящих слева – направо. Номера разрядов в ней убывают от (–1) слева – направо. При этом дробные числа в системах с постоянным основанием р разлагают при переводах по отрицательным (–1, –2, …)степеням р. Таким образом, запись Аp=0,–1–2 …–sв развернутой форме означает: Аp= –1p–1+–2p–2+…+–s p–s.
Пример 1. 0,4710 = 410–1 + 710–2; 0,2657 = 27–1 + 67–2 + 57–3.
Правильная дробь имеет нулевую целую часть. Результат перевода правильной дроби – всегда правильная дробь. Обыкновенной дробью называется ее представление в виде отношения целых чисел m/n, где m (числитель) – целое число, а n (знаменатель) – натуральное число.
Обыкновенные дроби также называют рациональными. Дроби, не представимые в виде отношения целых чисел m/n, называют иррациональными.
В позиционной системе счисления с основанием p правильная дробь имеет вид (0,–1–2 …–s), представляющий разложение числа по отрицательным (–1, –2, …) степеням p. Все величины, стоящие в разрядах дроби в системе с основанием p, как и у целых чисел, могут принимать значения от 0 до (p – 1).
Дроби, задающие рациональные числа, могут быть конечными и бесконечными (периодическими). У конечной дроби запись обрывается, например 0,2478. Бесконечная дробь помимо постоянной части (предпериода) имеет периодическую, которая теоретически повторяется в записи бесконечное число раз. Данную часть записи дроби называют периодом. В точной записи дроби данную часть записи приводят один раз в круглых скобках.
Пример 2. Бесконечная шестнадцатеричная дробь 0,В7С(2А)16 имеет предпериод В7С и период, равный 2А. Значение дроби можно представить бесконечной записью вида 0,В7С2А2А2А2А2А…16 = 0,В7С(2А)16.
Замечание. Конечные дроби могут быть представлены частным случаем бесконечных, у которых период равен нулю – (0).
Смешанным называют число со знаком, в котором явно выделены ненулевые целая и дробная части. Смешанные числа в зависимости от способа представления дробной части можно представлять в виде записи с обыкновенной дробью либо записи в позиционной систем счисления.
Пример 3. Смешанное число, приближающее число :
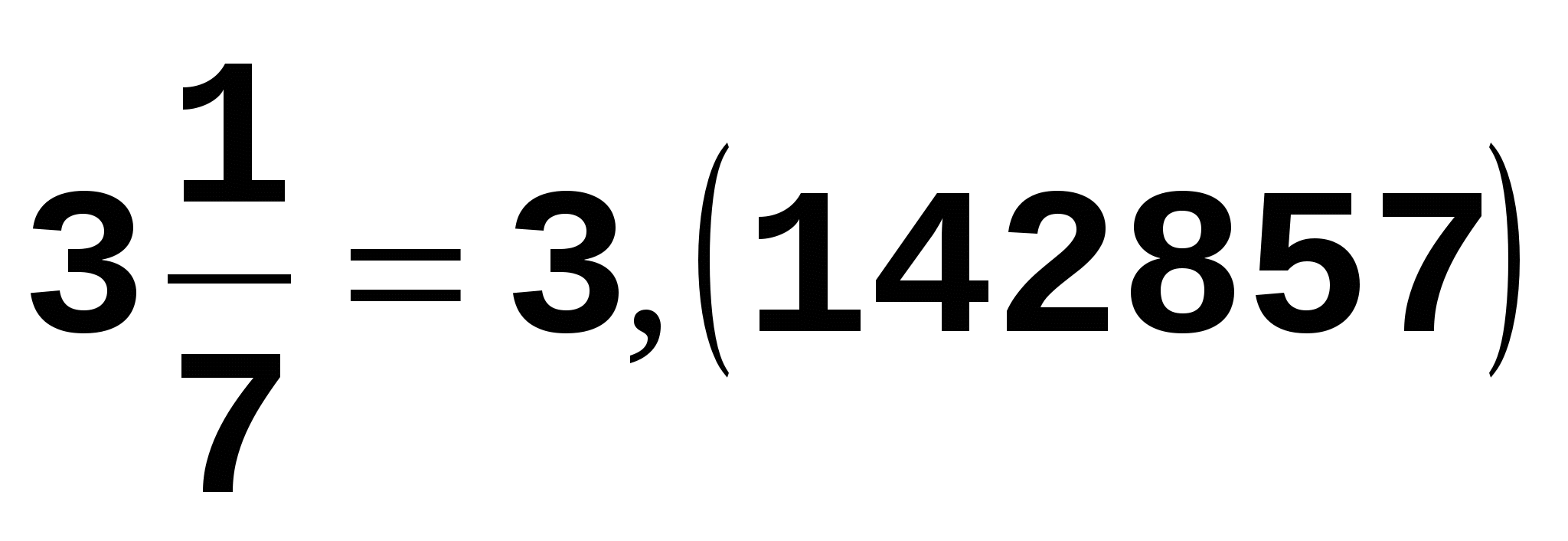 . .
Переводы смешанных чисел сводятся к отдельному переводу их целых и обыкновенных дробных частей.
|
 Скачать 9.96 Mb.
Скачать 9.96 Mb.